- 2021-04-14 发布 |
- 37.5 KB |
- 12页


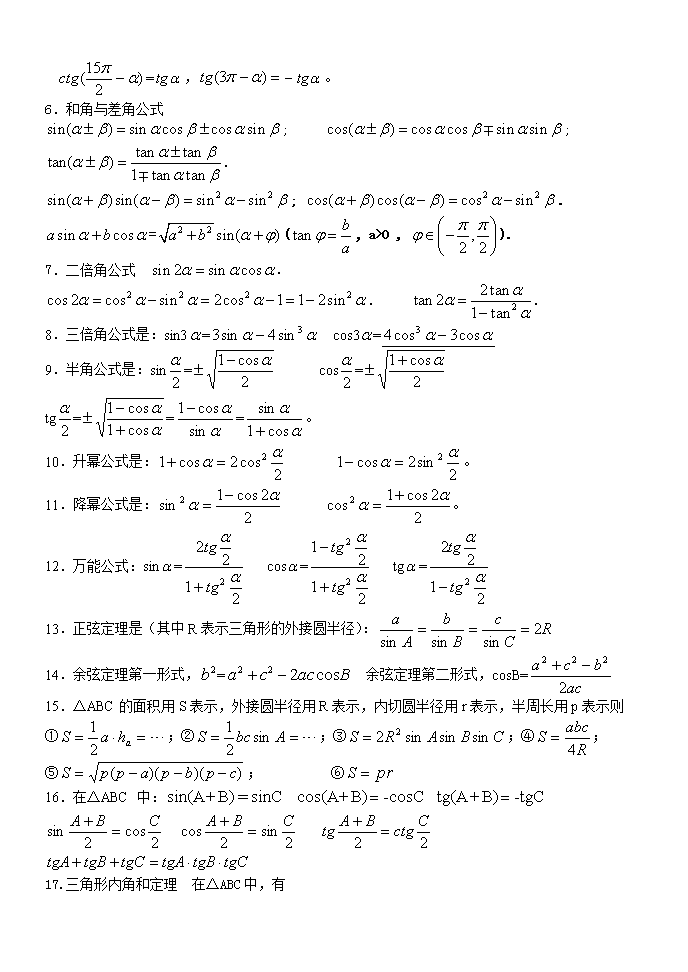
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高考数学常用基础知识点集萃
高中数学常用基础知识点集萃 一.集合函数 1.德摩根公式 . 2. . 3.若集合 A 中有 n 个元素,则集合 A 的所有不同的子集个数为 ,所有非空真子集的个数 是 。 4. 二次函数 的图象的对称轴方程是 ,顶点坐标是 。 二次函数的解析式的三种形式 ①一般式 ; ② 顶点式 ;③两点式 . 5.设 那么 上是增函数; 上是减函数. 设函数 在某个区间内可导,如果 ,则 为增函数;如果 ,则 为减函数. 6. 函 数 的 图 象 的 对 称 性 : ① 函 数 的 图 象 关 于 直 线 对 称 .②若函数 的图象与函数 对称则 其对称轴为 x= 7.两个函数图象的对称性:①函数 与函数 的图象关于直线 (即 轴)对称. ②函数 与函数 的图象关于直线 对称.③函数 和 的图象关于直线 y=x 对称. 8. 分 数 指 数 幂 ( , 且 ) . ( , 且 ). 9. . 10.对数的换底公式 .推论 . 二.数列 1. ( 数列 的前 n 项的和为 ). 2.等差数列的通项公式 ; 其前 n 项和公式 ( ) ; ( )U U U U U UC A B C A C B C A B C A C B= = U UA B A A B B A B C B C A= ⇔ = ⇔ ⊆ ⇔ ⊆ UA C B⇔ = Φ UC A B R⇔ = )( Nn ∈ n2 22 −n cbxaxy ++= 2 a bx 2 −= −− a bac a b 4 4 2 2 , 2( ) ( 0)f x ax bx c a= + + ≠ 2( ) ( ) ( 0)f x a x h k a= − + ≠ 1 2( ) ( )( )( 0)f x a x x x x a= − − ≠ [ ] 2121 ,, xxbaxx ≠∈⋅ [ ]1 2 1 2( ) ( ) ( ) 0x x f x f x− − > ⇔ [ ]1 2 1 2 ( ) ( ) 0 ( ) ,f x f x f x a bx x − > ⇔− 在 [ ]1 2 1 2( ) ( ) ( ) 0x x f x f x− − < ⇔ [ ]1 2 1 2 ( ) ( ) 0 ( ) ,f x f x f x a bx x − < ⇔− 在 )(xfy = 0)( >′ xf )(xf 0)( <′ xf )(xf ( )y f x= ( )y f x= x a= ( ) ( )f a x f a x⇔ + = − (2 ) ( )f a x f x⇔ − = ( )y f p= ( )z f q= 2 p q+ ( )y f x= ( )y f x= − 0x = y ( )y f mx a= − ( )y f b mx= − 2 a bx m += )(xfy = )(1 xfy −= 1m n n m a a = 0, ,a m n N ∗> ∈ 1n > 1m n m n a a − = 0, ,a m n N ∗> ∈ 1n > log ( 0, 1, 0)b a N b a N a a N= ⇔ = > ≠ > loglog log m a m NN a = ma log logn a nb bm = 1 1 , 1 , 2n n n s na s s n− == − ≥ { }na 1 2n ns a a a= + + + * 1 1( 1) ( )na a n d dn a d n N= + − = + − ∈ 1( ) 2 n n n a as += 1 ( 1) 2 n nna d −= + 3.等比数列的通项公式 ; 其前 n 项的和公式 或 . 4.当等比数列 的公比 q 满足 <1 时, =S= 。一般地,如果无穷数列 前 n 项和 的极限 存在,就把这个极限称为这个数列的各项和(或所有项的和),用 S 表示,即 S= 。 5.若 m、n、p、q∈N,且 ,那么:当数列 是等差数列时,有 ; 当数列 是等比数列时,有 。 6. 等 比 差 数 列 : 的 通 项 公 可 由 7.分期付款(按揭贷款) 每次还款 元(贷款 元, 次还清,每期利率为 ). 三.三角函数 1.以角 的顶点为坐标原点,始边为 x 轴正半轴建立直角坐标系,在角 的终边上任取一个异于原 点的点 ,点 P 到原点的距离记为 ,则 sin = ,cos = ,tg = ,ctg = ,sec = ,csc = 2.函数 的最大值是 ,最小值是 周期是 , 频 率 是 , 相 位 是 , 初 相 是 ; 其 图 象 的 对 称 轴 是 直 ,凡是该图象与直线 的交点都是该图象的对称中心。 3.三角函数的单调区间: 的递增区间是 ,递减区间是 ; 的递增区间是 ,递减区间是 , 的递增区间是 , 的递减 区间是 。 4.同角三角函数的基本关系式 , = , . 5.诱导公式可用十个字概括为:奇变偶不变,符号看象限。如: , 1 *1 1 ( )n n n aa a q q n Nq −= = ⋅ ∈ 1 1 (1 ) , 11 , 1 n n a q qs q na q − ≠= − = 1 1 , 11 , 1 n n a a q qqs na q − ≠ −= = { }na q nn S∞→lim q a −1 1 { }na nn S∞→lim nn S∞→lim qpnm +=+ { }na qpnm aaaa +=+ { }na qpnm aaaa ⋅=⋅ { }na k+ 1 1, ( 0)n na qa d a b q+ = + = ≠ ( )1 1n n n na k q a k a qa qk k+ ++ = + ⇔ = + − 1 dqk k d k q ∴ − = ⇒ = − (1 ) (1 ) 1 n n ab bx b += + − a n b α α ),( yxP r α r y α r x α x y α y x α x r α y r BxAy ++= )sin( ϕω ),(其中 00 >> ωA BA + AB − ω π2=T π ω 2 =f ϕω +x ϕ )(2 Zkkx ∈+=+ ππϕω By = xy sin= +− 2222 ππππ kk , )( Zk ∈ ++ 2 3222 ππππ kk , )( Zk ∈ xy cos= [ ]πππ kk 22 ,− )( Zk ∈ [ ]πππ +kk 22 , )( Zk ∈ tgxy = +− 22 ππππ kk , )( Zk ∈ ctgxy = ( )πππ +kk , )( Zk ∈ 2 2sin cos 1θ θ+ = tanθ θ θ cos sin tan 1cotθ θ⋅ = =− )2 3sin( απ αcos− = , 。 6.和角与差角公式 ; ; . ; . = ( ,a>0 , ). 7.二倍角公式 . . . 8.三倍角公式是:sin3 = cos3 = 9.半角公式是:sin = cos = tg = = = 。 10.升幂公式是: 。 11.降幂公式是: 。 12.万能公式:sin = cos = tg = 13.正弦定理是(其中 R 表示三角形的外接圆半径): 14.余弦定理第一形式, = 余弦定理第二形式,cosB= 15.△ABC 的面积用 S 表示,外接圆半径用 R 表示,内切圆半径用 r 表示,半周长用 p 表示则 ① ;② ;③ ;④ ; ⑤ ; ⑥ 16.在△ABC 中: 17.三角形内角和定理 在△ABC 中,有 )2 15( απ −ctg αtg =− )3( απtg αtg− sin( ) sin cos cos sinα β α β α β± = ± cos( ) cos cos sin sinα β α β α β± = tan tantan( ) 1 tan tan α βα β α β ±± = 2 2sin( )sin( ) sin sinα β α β α β+ − = − 2 2cos( )cos( ) cos sinα β α β α β+ − = − sin cosa bα α+ 2 2 sin( )a b α ϕ+ + tan b a ϕ = ,2 2 π πϕ ∈ − sin 2 sin cosα α α= 2 2 2 2cos2 cos sin 2cos 1 1 2sinα α α α α= − = − = − 2 2tantan 2 1 tan αα α= − α αα 3sin4sin3 − α αα cos3cos4 3 − 2 α 2 cos1 α−± 2 α 2 cos1 α+± 2 α α α cos1 cos1 + −± α α sin cos1− α α cos1 sin + 2cos2cos1 2 αα =+ 2sin2cos1 2 αα =− 2 2cos1sin 2 αα −= 2 2cos1cos2 αα += α 21 22 2 α α tg tg + α 21 21 2 2 α α tg tg + − α 21 22 2 α α tg tg − RC c B b A a 2sinsinsin === 2b Bacca cos222 −+ ac bca 2 222 −+ =⋅= ahaS 2 1 == AbcS sin2 1 CBARS sinsinsin2 2= R abcS 4 = ))()(( cpbpappS −−−= prS = -tgCB)+tg(A-cosCB)+cos(AsinC=B)+sin(A == 2cos2sin CBA =+ 2sin2cos CBA =+ 22 CctgBAtg =+ tgCtgBtgAtgCtgBtgA ⋅⋅=++ . 18.积化和差公式: ① ,② , ③ ,④ 19.和差化积公式: ① , ② , ③ , ④ 四.反三角函数 1. 的定义域是[-1,1],值域是 ,奇函数,增函数; 的定义域是[-1,1],值域是 ,非奇非偶,减函数; 的定义域是 R,值域是 ,奇函数,增函数; 的定义域是 R,值域是 ,非奇非偶,减函数。 2.当 对任意的 ,有: 当 。 五.平面向量 1.平面两点间的距离公式 ( ) 2 2 2 C A BA B C C A B ππ π ++ + = ⇔ = − + ⇔ = − 2 2 2( )C A Bπ⇔ = − + )]sin()[sin(2 1cossin βαβαβα −++=⋅ )]sin()[sin(2 1sincos βαβαβα −−+=⋅ )]cos()[cos(2 1coscos βαβαβα −++=⋅ )]cos()[cos(2 1sinsin βαβαβα −−+−=⋅ 2cos2sin2sinsin yxyxyx −⋅+=+ 2sin2cos2sinsin yxyxyx −⋅+=− 2cos2cos2coscos yxyxyx −⋅+=+ 2sin2sin2coscos yxyxyx −⋅+−=− xy arcsin= ]22[ ππ ,− xy arccos= ]0[ π, arctgxy = )22( ππ ,− arcctgxy = )0( π, xxxxx ==−∈ )cos(arccos)sin(arcsin]11[ ,时,, 2sin(arccos ) 1x x= − , 2cos(arcsin ) 1x x= − xxxx arccos)arccos(arcsin)arcsin( −=−−=− π, 2arccosarcsin π=+ xx Rx ∈ 2 )()( )()( π π =+ −=−−=− == arcctgxarctgx arcctgxxarcctgarctgxxarctg xarcctgxctgxarctgxtg , , xarctgxctgxarcctgxtgx 1)(1)(0 ==≠ ,时,有: = (A ,B ). 25.向量的平行与垂直 设 a= ,b= ,且 b 0,则 a b b=λa . a b(a 0) a·b=0 . 2.线段的定比分公式 设 , , 是线段 的分点, 是实数,且 ,则 3.三角形的重心坐标公式 △ABC 三个顶点的坐标分别为 、 、 ,则△ ABC 的重心的坐标是 . 4.点的平移公式 (图形 F 上的任意一点 P(x,y)在平 移后图形 上的对应点为 ,且 的坐标为 ). 六.不等式 1.常用不等式: (1) (当且仅当 a=b 时取“=”号). (2)两个正数的均值不等式是: 三个正数的均值不等式是: n 个正数的均值不等式是: (3) (4)柯西不等式 (5) 2.两个正数 的调和平均数、几何平均数、算术平均数、均方根之间的关系是 3.极值定理 已知 都是正数,则有 (1)如果积 是定值 ,那么当 时和 有最小值 ; (2)如果和 是定值 ,那么当 时积 有最大值 . 4.含有绝对值的不等式 当 a> 0 时,有 ,A Bd | |AB AB AB= ⋅ 2 2 2 1 2 1( ) ( )x x y y= − + − 1 1( , )x y 2 2( , )x y 1 1( , )x y 2 2( , )x y ≠ ⇔ 1 2 2 1 0x y x y⇔ − = ⊥ ≠ ⇔ 1 2 1 2 0x x y y⇔ + = 1 1 1( , )P x y 2 2 2( , )P x y ( , )P x y 1 2PP λ 1 2PP PPλ= 1 2 1 2 1 1 x xx y yy λ λ λ λ + = + + = + 1 1A(x ,y ) 2 2B(x ,y ) 3 3C(x ,y ) 1 2 3 1 2 3( , )3 3 x x x y y yG + + + + ' ' ' ' x x h x x h y y k y y k = + = − ⇔ = + = − ' 'OP OP PP⇔ = + 'F ' ' '( , )P x y 'PP ( , )h k ,a b R∈ ⇒ 2 2 2a b ab+ ≥ abba ≥+ 2 3 3 abccba ≥++ n n n aaan aaa 21 21 ≥+++ 3 3 3 3 ( 0, 0, 0).a b c abc a b c+ + ≥ > > > 2 2 2 2 2( )( ) ( ) , , , , .a b c d ac bd a b c d R+ + ≥ + ∈ bababa +≤+≤− ba、 2211 2 22 babaab ba +≤+≤≤ + yx, xy p yx = yx + p2 yx + s yx = xy 2 4 1 s . 或 . 5.无理不等式(1) . (2) . (3) . 6.指数不等式与对数不等式 (1)当 时, ; . (2)当 时, ; 七.解析几何 1. 直角坐标平面内的两点间距离公式: 2.斜率公式 ( 、 ).定义式为 k= . 3.直线的四种方程 (1)点斜式 (直线 过点 ,且斜率为 ). (2)斜截式 (b 为直线 在 y 轴上的截距). (3)两点式 ( )( 、 ( )). (4)截距式: (5)一般式 (其中 A、B 不同时为 0). 4. 经 过 两 条 直 线 的 交 点 的 直 线 系 方 程 是 : 5.两条直线的平行和垂直 (1)若 , ① ;② . (2)若 , ,且 A1、A2、B1、B2 都不为零, 22x a x a a x a< ⇔ < ⇔ − < < 2 2x a x a x a> ⇔ > ⇔ > x a< − ( ) 0 ( ) ( ) ( ) 0 ( ) ( ) f x f x g x g x f x g x ≥ > ⇔ ≥ > 2 ( ) 0 ( ) 0( ) ( ) ( ) 0 ( ) 0( ) [ ( )] f x f xf x g x g x g xf x g x ≥ ≥> ⇔ ≥ < > 或 2 ( ) 0 ( ) ( ) ( ) 0 ( ) [ ( )] f x f x g x g x f x g x ≥ < ⇔ > < 1a > ( ) ( ) ( ) ( )f x g xa a f x g x> ⇔ > ( ) 0 log ( ) log ( ) ( ) 0 ( ) ( ) a a f x f x g x g x f x g x > > ⇔ > > 0 1a< < ( ) ( ) ( ) ( )f x g xa a f x g x> ⇔ < ( ) 0 log ( ) log ( ) ( ) 0 ( ) ( ) a a f x f x g x g x f x g x > > ⇔ > < 2 21 2 2121 )()( yyxxPP −+−= 2 1 2 1 y yk x x −= − 1 1 1( , )P x y 2 2 2( , )P x y αtg 1 1( )y y k x x− = − l 1 1 1( , )P x y k y kx b= + l 1 1 2 1 2 1 y y x x y y x x − −=− − 1 2y y≠ 1 1 1( , )P x y 2 2 2( , )P x y 1 2x x≠ 1=+ b y a x 0Ax By C+ + = 00 22221111 =++=++ CyBxAlCyBxAl :和: 0)( 222111 =+++++ CyBxACyBxA λ 1 1 1:l y k x b= + 2 2 2:l y k x b= + 1 2 1 2 1 2,l l k k b b⇔ = ≠ 1 2 1 2 1l l k k⊥ ⇔ = − 1 1 1 1: 0l A x B y C+ + = 2 2 2 2: 0l A x B y C+ + = ① ;② ; 6.夹角公式 .( , , ) ( , , ). 直线 时,直线 l1 与 l2 的夹角是 . 7. ①点到直线的距离 (点 ,直线 : ). ②两条平行直线 距离是 8. 圆的四种方程 (1)圆的标准方程 . (2)圆的一般方程 ( >0). (3)圆的参数方程 . (4)圆的直径式方程 (直径的端点是 、 ). 9.经过两个圆 , 的交点的圆系方程 是: 经 过 直 线 与 圆 的 交 点 的 圆 系 方 程 是 : 10.圆 为切点的切线方程是 一 般 地 , 曲 线 为 切 点 的 切 线 方 程 是 : 。例如,抛物线 的以点 为切点的 切线方程是: ,即: 。 注意:这个结论只能用来做选择题或者填空题,若是做解答题,只能按照求切线方程的常规 过程去做。 11.椭圆 的参数方程是 . 12.椭圆 的焦点坐标是 ,准线方程是 ,离心率是 , 1 1 1 1 2 2 2 2 A B Cl l A B C ⇔ = ≠ 1 2 1 2 1 2 0l l A A B B⊥ ⇔ + = 2 1 2 1 tan | |1 k k k k α −= + 1 1 1:l y k x b= + 2 2 2:l y k x b= + 1 2 1k k ≠ − 1 2 2 1 1 2 1 2 tan A B A B A A B B α −= + 1 1 1 1: 0l A x B y C+ + = 2 2 2 2: 0l A x B y C+ + = 1 2 1 2 0A A B B+ ≠ 1 2l l⊥ 2 π 0 0 2 2 | |Ax By Cd A B + += + 0 0( , )P x y l 0Ax By C+ + = 00 2211 =++=++ CByAxlCByAxl :,: 22 21 BA CCd + −= 2 2 2( ) ( )x a y b r− + − = 2 2 0x y Dx Ey F+ + + + = 2 2 4D E F+ − cos sin x a r y b r θ θ = + = + 1 2 1 2( )( ) ( )( ) 0x x x x y y y y− − + − − = 1 1( , )A x y 2 2( , )B x y 0111 22 =++++ FyExDyx 0222 22 =++++ FyExDyx 0)( 222 22 111 22 =+++++++++ FyExDyxFyExDyx λ 0=++ CByAxl: 022 =++++ FEyDxyx 0)(22 =+++++++ CByAxFEyDxyx λ ),( 00 222 yxPryx 的以=+ 2 00 ryyxx =+ 2 2 0 00 ( )Ax Cy Dx Ey F P x y+ + + + = 的以点 , 0 0 0 0 02 2 x x y yAx x Cy y D E F + ++ + ⋅ + ⋅ + = xy 42 = )21( ,P 2 142 +×= xy 1+= xy 2 2 2 2 1( 0)x y a ba b + = > > cos sin x a y b θ θ = = 12 2 2 2 =+ b y a x )0( >> ba )0( ,c± c ax 2 ±= a ce = 通径的长是 。其中 。 13.椭圆 焦半径公式 , . 14.双曲线标准方程的两种形式是: 和 。 15.双曲线 的焦点坐标是 ,准线方程是 ,离心率是 ,通径的长 是 ,渐近线方程是 。其中 。 16.双曲线 的焦半径公式 , . 17.抛物线 的焦点坐标是: ,准线方程是: 。若点 是抛物线 上一点,则该点到抛物线的焦点的距离(称为焦半径)是: ,过该抛物线的焦 点且垂直于抛物线对称轴的弦(称为通径)的长是: 。 18.抛物线 上的动点可设为 P 或 P ,其中 . 19.二次函数 的图象是抛物线:(1)顶点坐标为 ;(2)焦点的坐标为 ;(3)准线方程是 . 20.直线与圆锥曲线相交的弦长公式 或 (弦端点 A ,由 方程 消去 y 得到 , , 为直线 的倾斜角, 为直线的斜 率). 21. 与 双 曲 线 共 渐 近 线 的 双 曲 线 系 方 程 是 。 与 双 曲 线 共焦点的双曲线系方程是 。 22.圆锥曲线的两类对称问题: (1)曲线 关于点 成中心对称的曲线是 . (2)曲线 关于直线 成轴对称的曲线是 a b22 222 bac −= 2 2 2 2 1( 0)x y a ba b + = > > 2 1 0( )aPF e x c = + 2 2 0( )aPF e xc = − 12 2 2 2 =− b y a x 12 2 2 2 =− b x a y )00( >> ba , 12 2 2 2 =− b y a x )0( ,c± c ax 2 ±= a ce = a b22 02 2 2 2 =− b y a x 222 bac += 2 2 2 2 1( 0, 0)x y a ba b − = > > 2 1 0| ( ) |aPF e x c = + 2 2 0| ( ) |aPF e xc = − pxy 22 = 02 ,p 2 px −= ),( 00 yxP pxy 22 = 20 px + p2 pxy 22 = ),2( 2 yp y 或)2,2( 2 ptptP ( , )x y 2 2y px= 2 2 2 4( )2 4 b ac by ax bx c a x a a −= + + = + + ( 0)a ≠ 24( , )2 4 b ac b a a −− 24 1( , )2 4 b ac b a a − +− 24 1 4 ac by a − −= 2 2 1 2 1 2( ) ( )AB x x y y= − + − 2 2 2 1 2 1 2(1 ) | | (1 ) | | 1 tanAB k x x k x xa α∆= + − = + ⋅ = − + ),(),,( 2211 yxByx = += 0)y,x(F bkxy 02 =++ cbxax 0∆ > α AB k 12 2 2 2 =− b y a x λ=− 2 2 2 2 b y a x )0( ≠λ 12 2 2 2 =− b y a x 12 2 2 2 =−−+ kb y ka x ( , ) 0F x y = 0 0( , )P x y 0 0(2 - ,2 ) 0F x x y y− = ( , ) 0F x y = 0Ax By C+ + = . 23.“四线”一方程 对于一般的二次曲线 ,用 代 ,用 代 ,用 代 ,用 代 ,用 代 即得方程 ,曲线的切线,切点弦,中点弦,弦中 点方程均是此方程得到. 八.立体几何 1.共线向量定理 对空间任意两个向量 a、b(b≠0 ),a∥b 存在实数λ使 a=λb. 2.对空间任一点 O 和不共线的三点 A、B、C,满足 ,则四点 P、A、B、C 是共面 . 3. 空间两个向量的夹角公式 cos〈a,b〉= (a= ,b= ). 4.直线 与平面所成角 ( 为平面 的法向量). 5.二面角 的平面角 或 ( , 为平面 , 的法 向量). 6.设 AC 是α内的任一条直线,且 BC⊥AC,垂足为 C,又设 AO 与 AB 所成的角为 ,AB 与 AC 所成的 角为 ,AO 与 AC 所成的角为 .则 . 7.空间两点间的距离公式 若 A ,B ,则 = . 8.点 到直线 距离 (点 在直线 上,直线 的方向向量 a= ,向量 b= ). 9.异面直线间的距离 ( 是两异面直线,其公垂向量为 , 分别是 上任一 点, 为 间的距离). 10.点 到平面 的距离 ( 为平面 的法向量, 是面 的一条斜线, ). 11.异面直线上两点距离公式 (两条异面直线 a、b 所成的角为θ,其公垂线段 的长度为 h.在直线 a、b 上分别取两点 E、F, , , ). 12. 2 2 2 2 2 ( ) 2 ( )( , ) 0A Ax By C B Ax By CF x yA B A B + + + +− − =+ + 2 2 0Ax Bxy Cy Dx Ey F+ + + + + = 0x x 2x 0y y 2y 0 0 2 x y xy+ xy 0 2 x x+ x 0 2 y y+ y 0 0 0 0 0 0 02 2 2 x y xy x x y yAx x B Cy y D E F + + ++ ⋅ + + ⋅ + ⋅ + = ⇔ OP xOA yOB zOC= + + ⇔ 1x y z+ + = 1 1 2 2 3 3 2 2 2 2 2 2 1 2 3 1 2 3 a b a b a b a a a b b b + + + + + + 1 2 3( , , )a a a 1 2 3( , , )b b b AB sin | || | AB marc AB m β ⋅= m α lα β− − cos | || | m narc m n θ ⋅= cos | || | m narc m n π ⋅− m n α β 1 θ 2 θ θ 1 2cos cos cosθ θ θ= 1 1 1( , , )x y z 2 2 2( , , )x y z ,A Bd | |AB AB AB= ⋅ 2 2 2 2 1 2 1 2 1( ) ( ) ( )x x y y z z= − + − + − Q l 2 21 (| || |) ( )| |h a b a ba = − ⋅ P l l PA PQ | | | | CD nd n ⋅= 1 2,l l n C D、 1 2,l l d 1 2,l l B α | | | | AB nd n ⋅= n α AB α A α∈ 2 2 2 2 cosd d m n mn θ= + + − 'AA 'A E m= AF n= EF d= 2 2 2 2 1 2 3l l l l= + + 2 2 2 1 2 3cos cos cos 1θ θ θ⇔ + + = (长度为 的线段在三条两两互相垂直的直线上的射影长分别为 ,夹角分别为 ) (立几中长方体对角线长的公式是其特例). 13. 面积射影定理 (平面多边形及其射影的面积分别是 、 ,它们所在平面所成锐二 面角的为 ). 14.欧拉定理(欧拉公式) (简单多面体的顶点数 V、棱数 E 和面数 F) 15.球的半径是 R,则其体积是 ,其表面积是 . 九.排列组合、二项式定理 1.分类计数原理(加法原理) . 2.分步计数原理(乘法原理) . 3.排列数公式 = = .( , ∈N*,且 ). 4.组合数公式 = = = ( , ∈N*,且 ). 5.组合数的两个性质(1) = ;(2) + = 6.组合恒等式 . 7.排列数与组合数的关系是: . 8.二项式定理 ; 二项展开式的通项公式: . 9.等可能性事件的概率 . 10.互斥事件 A,B 分别发生的概率的和 P(A+B)=P(A)+P(B). 11. 个互斥事件分别发生的概率的和 P(A1+A2+…+An)=P(A1)+P(A2)+…+P(An). 12.独立事件 A,B 同时发生的概率 P(A·B)= P(A)·P(B). 13.n 个独立事件同时发生的概率 P(A1· A2·…· An)=P(A1)· P(A2)·…· P(An). 14.n 次独立重复试验中某事件恰好发生 k 次的概率 15.数学期望 16.数学期望的性质:(1) ;(2)若 ~ ,则 . 17.方差 18.标准差 = . 19. 方 差 的 性 质 (1) ;(2) ; ( 3 ) 若 ~ , 则 . 十.极限与导数,复数 l 1 2 3l l l、 、 1 2 3 θ θ θ、 、 ' cos S S θ = S 'S θ 2V F E+ − = 34 3V Rπ= 24S Rπ= 1 2 nN m m m= + + + 1 2 nN m m m= × × × m nA )1()1( +−− mnnn ! ! )( mn n − n m m n≤ m nC m n m m A A m mnnn ××× +−− 21 )1()1( !! ! )( mnm n −⋅ n m m n≤ m nC mn nC − m nC 1−m nC m nC 1+ 1 121 + +++ =++++ r n r n r r r r r r CCCCC m m n nA = m!×C nn n rrnr n n n n n n n n bCbaCbaCbaCaCba ++++++=+ −−− 222110)( rrnr nr baCT − + =1 )210( nr ,,, = ( ) mP A n = n ( ) (1 ) .k k n k n nP k C P P −= − 1 1 2 2 n nE x P x P x Pξ = + + + + ( ) ( )E a b aE bξ ξ+ = + ξ ( , )B n p E npξ = ( ) ( ) ( )2 2 2 1 1 2 2 n nD x E p x E p x E pξ ξ ξ ξ= − ⋅ + − ⋅ + + − ⋅ + σξ ξD ( ) 2 2( )D E Eξ ξ ξ= − ( ) 2D a b a Dξ ξ+ = ξ ( , )B n p (1 )D np pξ = − 1.特殊数列的极限 (1) . (2) . (3) ( 无穷等比数列 ( )的和). 2. .这是函数极限存在的一个充要条件. 3. 在 处的导数 . 4.瞬时速度 . 5.瞬时加速度 . 6. 在 的导数 . 7.函数 在点 处的导数是曲线 在 处的切线的斜率 ,相应的 切线方程是 . 8.几种常见函数的导数 (1) (C 为常数). (2) . (3) . (4) . (5) ; . (6) ; . 9.复合函数的求导法则 设函数 在点 处有导数 ,函数 在点 处的对 应点 U 处有导数 ,则复合函数 在点 处有导数,且 ,或写作 . 10. .( ) 11.复数 的模(或绝对值) = = . 12.复数的四则运算法则 (1) ; (2) ; (3) (4) . 13. 复 平 面 上 的 两 点 间 的 距 离 公 式 ( , 0 | | 1 lim 1 1 | | 1 1 n n q q q q q →∞ < = = < = −不存在 或 1 1 0 1 1 0 0 ( ) lim ( ) ( ) k k k k t t tn t t k k t a n a n a a k tb n b n b b k t − − −→∞ − < + + + = =+ + + > 不存在 ( )1 1 1 lim 1 1 n n a q aS q q→∞ − = =− − S }{ 1 1 na q − | | 1q < 0 lim ( ) x x f x a→ = ⇔ 0 0 lim ( ) lim ( ) x x x x f x f x a− +→ → = = )(xf 0x 0 0 0 0 0 0 ( ) ( )( ) lim limx x x x f x x f xyf x y x x= ∆ → ∆ → + ∆ −∆′ ′= = =∆ ∆ 0 0 ( ) ( )( ) lim lim t t s s t t s ts t t t υ ∆ → ∆ → ∆ + ∆ −′= = =∆ ∆ 0 0 ( ) ( )( ) lim lim t t v v t t v ta v t t t∆ → ∆ → ∆ + ∆ −′= = =∆ ∆ )(xf ),( ba ( )f x y′ ′= 0 0 ( ) ( )lim lim x x y f x x f x x x∆ → ∆ → ∆ + ∆ −= =∆ ∆ )(xfy = 0x )(xfy = ))(,( 00 xfxP )( 0xf ′ ))(( 000 xxxfyy −′=− 0=′C ' 1( ) ( )n nx nx n Q−= ∈ xx cos)(sin =′ xx sin)(cos −=′ xx 1)(ln =′ 1(log ) ln xa x a ′ = xx ee =′)( aaa xx ln)( =′ ( )u xϕ= x ' ' ( )xu xϕ= )(ufy = x ' ' ( )uy f u= ( ( ))y f xϕ= x ' ' ' x u xy y u= ⋅ ' ' '( ( )) ( ) ( )xf x f u xϕ ϕ= ,a bi c di a c b d+ = + ⇔ = = , , ,a b c d R∈ z a bi= + | |z | |a bi+ 2 2a b+ ( ) ( ) ( ) ( )a bi c di a c b d i+ + + = + + + ( ) ( ) ( ) ( )a bi c di a c b d i+ − + = − + − ( )( ) ( ) ( )a bi c di ac bd bc ad i+ + = − + + 2 2 2 2( ) ( ) ac bd bc ada bi c di ic d c d + −+ ÷ + = ++ + ( 0)c di+ ≠ 2 2 1 2 2 1 2 1| | ( ) ( )d z z x x y y= − = − + − 1 1 1z x y i= + ). 14.向量的垂直 非零复数 , 对应的向量分别是 , ,则 的实部为零 为纯虚数 (λ为非零实数). 15.实系数一元二次方程的解 实系数一元二次方程 ,①若 ,则 ;②若 ,则 ;③若 ,它在实 数 集 内 没 有 实 数 根 ; 在 复 数 集 内 有 且 仅 有 两 个 共 轭 复 数 根 . 16.棣莫佛定理是: 2 2 2z x y i= + 1z a bi= + 2z c di= + 1OZ 2OZ 1 2OZ OZ⊥ ⇔ 1 2z z⋅ ⇔ 2 1 z z ⇔ 2 2 2 1 2 1 2| | | | | |z z z z+ = + ⇔ 2 2 2 1 2 1 2| | | | | |z z z z− = + ⇔ 1 2 1 2| | | |z z z z+ = − ⇔ 0ac bd+ = ⇔ 1 2z izλ= 2 0ax bx c+ + = 2 4 0b ac∆ = − > 2 1,2 4 2 b b acx a − ± −= 2 4 0b ac∆ = − = 1 2 2 bx x a = = − 2 4 0b ac∆ = − < R C 2 2( 4 ) ( 4 0)2 b b ac ix b aca − ± − −= − < [ ] ))(sin(cos)sin(cos Znninrir nn ∈+=+ θθθθ查看更多