2021版高考数学一轮复习第二章函数及其应用2-7函数的图象练习苏教版

2021版高考数学一轮复习第二章函数及其应用2-7函数的图象练习苏教版

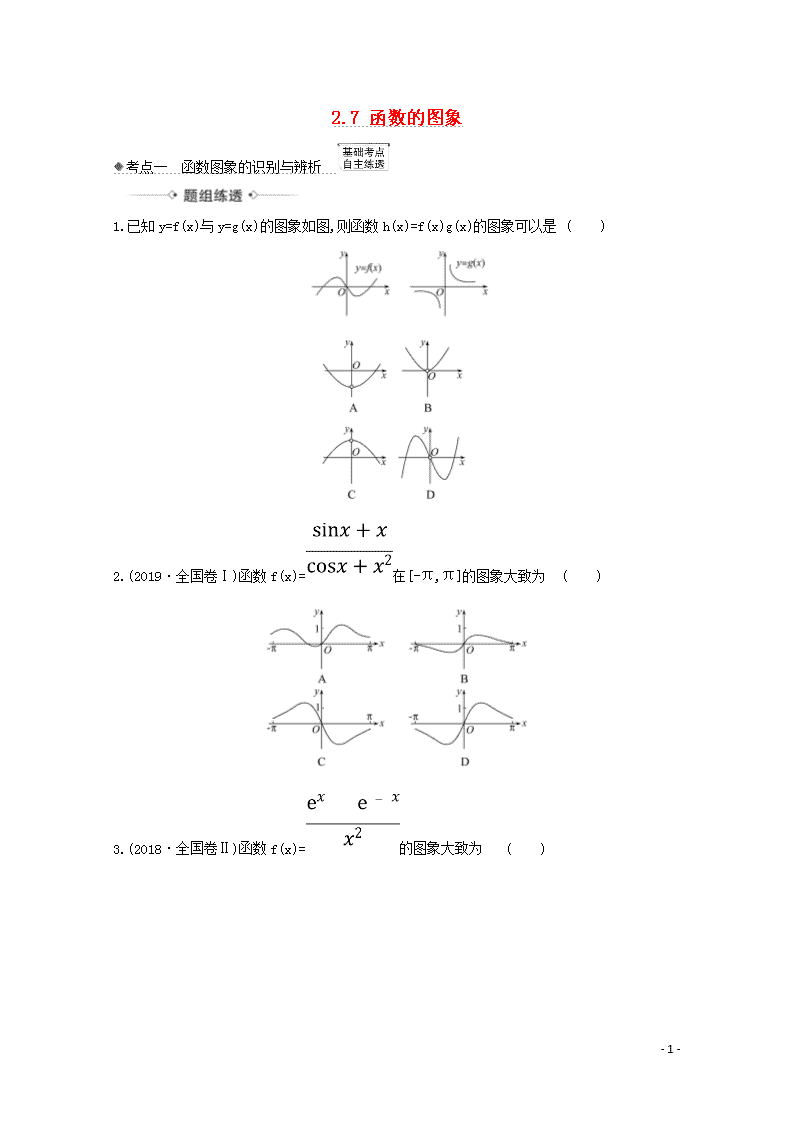
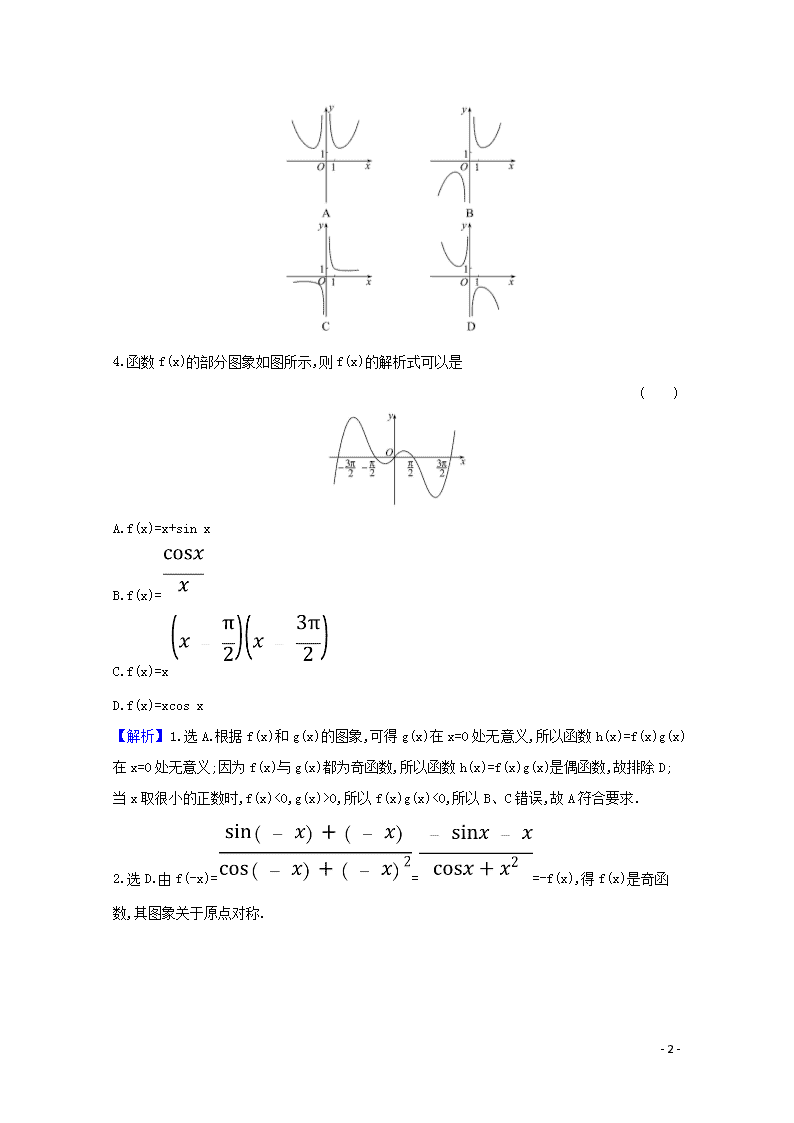
‎2.7 函数的图象 考点一　函数图象的识别与辨析 ‎ ‎1.已知y=f(x)与y=g(x)的图象如图,则函数h(x)=f(x)g(x)的图象可以是 (　　)‎ ‎2.(2019·全国卷Ⅰ)函数f(x)=在[-π,π]的图象大致为 (　　)‎ ‎3.(2018·全国卷Ⅱ)函数f(x)=的图象大致为 (　　)‎ - 10 -‎ ‎4.函数f(x)的部分图象如图所示,则f(x)的解析式可以是 ‎ ‎(　　)‎ A.f(x)=x+sin x B.f(x)=‎ C.f(x)=x D.f(x)=xcos x ‎【解析】1.选A.根据f(x)和g(x)的图象,可得g(x)在x=0处无意义,所以函数h(x)=f(x)g(x)在x=0处无意义;因为f(x)与g(x)都为奇函数,所以函数h(x)=f(x)g(x)是偶函数,故排除D;当x取很小的正数时,f(x)<0,g(x)>0,所以f(x)g(x)<0,所以B、C错误,故A符合要求.‎ ‎2.选D.由f(-x)===-f(x),得f(x)是奇函数,其图象关于原点对称.‎ - 10 -‎ 又f==>1,f(π)=>0.故选D.‎ ‎3.选B.因为x≠0,f(-x)==-f(x),‎ 所以f(x)为奇函数,舍去选项A,‎ 因为f(1)=e-e-1>0,所以舍去选项D;‎ 因为f'(x)=‎ ‎=,‎ 所以x>2,f'(x)>0,‎ 所以舍去选项C.‎ ‎4.选D.函数为奇函数,排除C;函数f(x)=x+sin x只有一个零点,排除A;B选项中x≠0,所以B不正确.‎ ‎　辨析函数图象的入手点 ‎(1)从函数的定义域,判断图象的左右位置;从函数的值域,判断图象的上下位置.‎ ‎(2)从函数的单调性,判断图象的变化趋势.‎ ‎(3)从函数的奇偶性,判断图象的对称性.‎ ‎(4)从函数的周期性,判断图象的循环往复.‎ ‎(5)从函数的特征点,排除不合要求的图象.‎ 考点二　作函数的图象 ‎ ‎【典例】分别作出下列函数的图象:‎ ‎(1)y=|lg x|.‎ ‎(2)y=2x+2.‎ ‎(3)y=x2-2|x|-1.‎ - 10 -‎ ‎【解题导思】‎ 序号 联想解题 ‎(1)由y=|lg x|,想到y=lg x的图象 ‎(2)由y=2x+2,想到y=2x的图象以及图象的平移变换 ‎(3)由y=x2-2|x|-1,想到二次函数的图象以及偶函数图象的特点 ‎【解析】(1)y=图象如图①所示.‎ ‎(2)将y=2x的图象向左平移2个单位.图象如图②所示.‎ ‎(3)y=图象如图③所示.‎ ‎　作函数图象的两种常用方法 ‎(1)直接法:当函数表达式(或变形后的表达式)是熟悉的基本初等函数时,就可根据这些函数的特征直接作出.‎ ‎(2)图象变换法:若函数图象可由某个基本初等函数的图象经过平移、翻折、对称得到,可利用图象变换作出,但要注意变换顺序.‎ ‎1.作出下列各函数的图象:‎ ‎(1)y=x-|x-1|.　　　　(2)y=.‎ ‎(3)y=|log2x-1|.‎ ‎【解析】(1)根据绝对值的意义,可将函数式化为分段函数y=可见其图象是由两条射线组成,如图(1)所示.‎ - 10 -‎ ‎(2)作出y=的图象,保留y=的图象中x≥0的部分,加上y=的图象中x>0部分关于y轴的对称部分,即得y=的图象,如图(2)实线部分.‎ ‎(3)先作出y=log2x的图象,再将其图象向下平移一个单位,保留x轴上方的部分,将x轴下方的图象翻折到x轴上方,即得y=|log2x-1|的图象,如图(3)所示.‎ ‎2.为了得到函数f(x)=log2x的图象,只需将函数g(x)=log2的图象________. ‎ ‎【解析】g(x)=log2=log2x-3=f(x)-3,因此只需将函数g(x)的图象向上平移3个单位即可得到函数f(x)=log2x的图象.‎ 答案:向上平移3个单位 考点三　函数图象的应用 ‎ 命 题 精 解 读 考什么:(1)作函数图象、识别函数图象、由图象求解析式、解方程、解不等式、求参数值等问题.‎ ‎(2)考查数学运算、直观想象、逻辑推理等核心素养.‎ 怎么考:多以选择、填空题的形式考查,考查学生的数学素养、数形结合思想、灵活运用知识的能力以及分析问题解决问题的能力.‎ 新趋势:以函数图象与性质为载体,图象与性质、数与形、求参数值或范围交汇考查.‎ - 10 -‎ 学 霸 好 方 法 ‎1.利用函数的图象研究函数的性质的四种对应关系 ‎(1)图象的左右范围对应定义域.‎ ‎(2)上下范围对应值域.‎ ‎(3)上升、下降趋势对应单调性.‎ ‎(4)对称性对应奇偶性 ‎2.利用函数的图象确定方程的根或不等式的解集的方法:‎ ‎(1)方程f(x)=g(x)的根就是函数f(x)与g(x)图象交点的横坐标;‎ ‎(2)不等式f(x)0)得ln x=(x>0),即ln x=(x>0).令y1=ln x(x>0),‎ ‎ ‎ y2=(x>0),在同一直角坐标系内画出函数y1,y2的图象,图象如图所示.根据图象可知两函数只有一个交点,所以原方程实根的个数为1.‎ 答案:1‎ 方程f(x)=g(x)的解的个数与函数y=f(x),y=g(x)的图象有何关系?‎ 提示:函数y=f(x)与y=g(x)图象交点的个数就是方程f(x)=g(x)的解的个数.‎ - 10 -‎ ‎1.(2020·大连模拟)下列函数f(x)的图象中,满足f>f(3)>f(2)的只可能是 ‎(　　)‎ ‎【解析】选D.因为f>f(3)>f(2),所以函数f(x)有增有减,排除A,B.在C中,ff(0),即f1.‎ 答案:(1,+∞)‎ ‎3.设函数f(x)=|x+a|,g(x)=x-1,对于任意的x∈R,不等式f(x)≥g(x)恒成立,则实数a的取值范围是________. ‎ ‎【解析】如图作出函数f(x)=|x+a|与g(x)=x-1的图象,观察图象可知:当且仅当-a≤1,即a≥-1时,不等式f(x)≥g(x)恒成立,因此a的取值范围是[-1,+∞).‎ - 10 -‎ 答案:[-1,+∞)‎ ‎1.已知函数y=的图象与函数y=kx的图象恰有两个交点,则实数k的取值范围是________. ‎ ‎【解析】函数y=的定义域为{x|x≠1},所以当x>1时,y=x+1,当-10,所以f(x)=-x+3<3,g(x)=log2x∈R,分别作出函数f(x)=-x+3和g(x)=log2x的图象,结合函数f(x)=-x+3和g(x)=log2x的图象可知,h(x)=min{f(x),g(x)}的图象,在这两个函数的交点处h(x)取得最大值.‎ 解方程组得 所以函数h(x)=min{f(x),g(x)}的最大值是1.‎ - 10 -‎ 答案:1‎ - 10 -‎