备战2014高考数学 高频考点归类分析（真题为例）：逻辑推理

备战2014高考数学 高频考点归类分析（真题为例）：逻辑推理

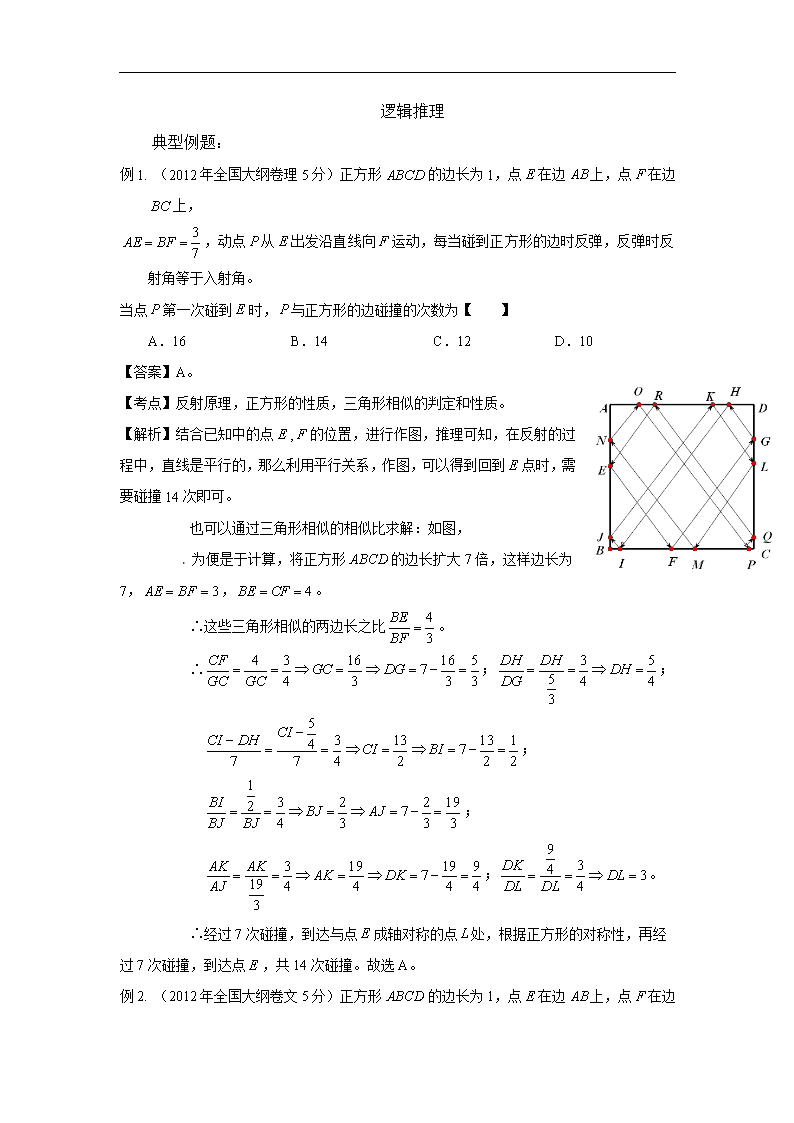
逻辑推理 典型例题： ‎ 例1. （2012年全国大纲卷理5分）正方形的边长为1，点在边上，点在边上，‎ ‎，动点从出发沿直线向运动，每当碰到正方形的边时反弹，反弹时反射角等于入射角。‎ 当点第一次碰到时，与正方形的边碰撞的次数为【 】‎ A．16 B．‎14 ‎‎ C．12 D．10‎ ‎【答案】A。‎ ‎【考点】反射原理，正方形的性质，三角形相似的判定和性质。‎ ‎【解析】结合已知中的点,的位置，进行作图，推理可知，在反射的过程中，直线是平行的，那么利用平行关系，作图，可以得到回到点时，需要碰撞14次即可。‎ ‎ 也可以通过三角形相似的相似比求解：如图，‎ ‎ 为便是于计算，将正方形的边长扩大7倍，这样边长为7，，。‎ ‎ ∴这些三角形相似的两边长之比。‎ ‎ ∴；；‎ ‎；‎ ‎；‎ ‎；。‎ ‎ ∴经过7次碰撞，到达与点成轴对称的点处，根据正方形的对称性，再经过7次碰撞，到达点，共14次碰撞。故选A。‎ 例2. （2012年全国大纲卷文5分）正方形的边长为1，点在边上，点在边 上，‎ ‎，动点从出发沿直线向运动，每当碰到正方形的边时反弹，反弹时反射角等于入射角。‎ 当点第一次碰到时，与正方形的边碰撞的次数为【 】‎ A 8 B ‎6 C 4 D 3‎ ‎【答案】B。‎ ‎【考点】反射原理，正方形的性质，三角形相似的判定和性质。‎ ‎【解析】结合已知中的点,的位置，进行作图，推理可知，在反射的过程中，直线是平行的，那么利用平行关系，作图，可以得到回到点时，需要碰撞6次即可。‎ ‎ 也可以通过三角形相似的相似比求解：如图，‎ ‎ 为便是于计算，将正方形的边长扩大3倍，这样边长为7，，。‎ ‎ ∴这些三角形相似的两边长之比。‎ ‎ ∴；；‎ ‎ ∴经过3次碰撞，到达与点成轴对称的点处，根据正方形的对称性，再经过3次碰撞，到达点，共6次碰撞。故选B。‎ 例3. （2012年江西省理5分）观察下列各式：则【 】‎ A．28 B．76 C．123 D．199‎ ‎【答案】C。‎ ‎【考点】归纳推理的思想方法。‎ ‎【解析】观察各等式的右边,它们分别为1，3，4，7，11，…，发现从第3项开始，每一项就是它的前两项之和，故等式的右边依次为1，3，4，7，11，18，29，47，76，123,…，故。故选C。‎ 例4. （2012年福建省文5分）数列{an}的通项公式an＝ncos，其前n项和为Sn，则S2 012等于【 】‎ A．1006 B．‎2012 C．503 D．0‎ ‎【答案】A。‎ ‎【考点】规律探索题。‎ ‎【解析】寻找规律：a1＝1cos＝0，a2＝2cosπ＝－2，a3＝3cos＝0，a4＝4cos2π＝4；‎ a5＝5cos＝0，a6＝6cos3π＝－6，a7＝7cos＝0，a8＝8cos＝8；‎ ‎······‎ ‎∴该数列每四项的和。‎ ‎∵2012÷4=503，∴S2 012＝2×503＝1006。故选A。‎ 例5. （2012年北京市理5分）已知，若同时满足条件：[来源:学科网]‎ ‎，‎ 则m的取值范围是 ▲ ‎ ‎【答案】。‎ ‎【考点】简易逻辑，函数的性质。‎ ‎【解析】由得。‎ ‎ ∵条件，∴当时，。‎ ‎ 当时，，不能做到在时，，所以舍去。‎ ‎ ∵作为二次函数开口只能向下，∴，且此时两个根为。‎ ‎ 为保证条件①成立，必须。‎ ‎ 又由条件的限制，可分析得出时，恒负。‎ ‎ ∴就需要在这个范围内有得正数的可能，即－4应该比两根中小的那个大。‎ ‎ 由得，‎ ‎ ∴当时，，解得交集为空集，舍去。‎ ‎ 当时，两根同为－2＞－4，舍去。‎ 当时，。‎ 综上所述，。‎ 例6. （2012年湖北省文5分）传说古希腊毕达哥拉斯学派的数学家经常在沙滩上面画点或用小石子表示数。他们研究过如图所示的三角形数：‎ 将三角形数1,3， 6,10，…记为数列，将可被5整除的三角形数按从小到大的顺序组成一个新数列，可以推测：‎ ‎（Ⅰ）是数列中的第　　▲　　项；‎ ‎（Ⅱ） =　　▲　　。（用表示）‎ ‎【答案】（Ⅰ）5030；（Ⅱ）。‎ ‎【考点】归纳规律。‎ ‎【解析】由以上规律可知三角形数1,3,6,10,…,的一个通项公式为，写出其若干项有：1,3,6,10,15,21,28,36,45,55,66,78,91,105,110,发现其中能被5整除的为 ‎10,15,45,55,105,110。‎ 故。‎ 从而由上述规律可猜想：（为正整数），‎ ‎。‎ 故,即是数列中的第5030项。[来源:Zxxk.Com]‎ 例7. （2012年湖南省理5分）设N=2n（n∈N*，n≥2），将N个数x1,x2,…，xN依次放入编号为1,2，…，N的N个位置，得到排列P0=x1x2…xN.将该排列中分别位于奇数与偶数位置的数取出，并按原顺序依次放入对应的前和后个位置，得到排列P1=x1x3…xN-1x2x4…xN，将此操作称为C变换，将P1分成两段，每段个数，并对每段作C变换，得到；当2≤i≤n-2时，将Pi分成2i段，每段个数，并对每段C变换，得到Pi+1，例如，当N=8时，P2=x1x5x3x7x2x6x4x8，此时x7位于P2中的第4个位置.‎ ‎（1）当N=16时，x7位于P2中的第 ▲ 个位置；‎ ‎（2）当N=2n（n≥8）时，x173位于P4中的第 ▲ 个位置.‎ ‎【答案】（1）6；（2）。‎ ‎【考点】演绎推理的基本方法，进行简单的演绎推理。‎ ‎【解析】（1）当N=16时, ‎ ‎,可设为,‎ ‎,即为,‎ ‎,即, x7位于P2中的第6个位置。‎ ‎（2）考察C变换的定义及（1）计算可发现：‎ 第一次C变换后，所有的数分为两段，每段的序号组成公差为2的等差数列，且第一段序号以1为首项，第二段序号以2为首项；‎ 第二次C变换后，所有的数据分为四段，每段的数字序号组成以为4公差的等差数列，且第一段的序号以1为首项，第二段序号以3为首项，第三段序号以2为首项，第四段序号以4为首项；‎ 依此类推可得出P4中所有的数字分为16段，每段的数字序号组成以16为公差的等差数列，且一到十六段的首项的序号分别为1，9，5，13，…，由于173=16×10+13，故x173位于以13为首项的那一段的第11个数，由于N=2n（n≥8）故每段的数字有2n-4个，以13为首项的是第四段，故x173位于第个位置。‎ 例8. （2012年福建省理4分）数列{an}的通项公式，前n项和为Sn，则S2 012＝ ▲ .‎ ‎【答案】3018。‎ ‎【考点】规律探索题。‎ ‎【解析】寻找规律：a1＝1cos＋1＝1，a2＝2cosπ＋1＝－1，a3＝3cos＋1＝1，a4＝4cos2π＋1＝5；‎ a5＝5cos＋1＝1，a6＝6cos3π＋1＝－5，a7＝7cos＋1＝1，a8＝8cos＋1＝9；‎ ‎······‎ ‎∴该数列每四项的和。‎ ‎∵2012÷4=503，∴S2 012＝6×503＝3018。‎ 例9. （2012年福建省文4分）某地区规划道路建设，考虑道路铺设方案，方案设计图中，点表示城市，两点之间连线表示两城市间可铺设道路，连线上数据表示两城市间铺设道路的费用．要求从任一城市都能到达其余各城市，并且铺设道路的总费用最小，例如：在三个城市道路设计中，若城市间可铺设道路的线路图如图①，则最优设计方案如图②，此时铺设道路的最小总费用为10.‎ 现给出该地区可铺设道路的线路图如图③，则铺设道路的最小总费用为 ▲ ．‎ ‎【答案】16。‎ ‎【考点】最优设计方案。‎ ‎【解析】根据题意先选择中间最优线路，中间有三条，分别是A→F→G→D，E→F→B，E→G→C，费用最低的是A→F→G→D为3＋1＋2＝6；再选择A→F→G→D线路到点E 的最低费用线路是：A→E费用为2；再选择A→F→G→D到C→B的最低费用，则选择：G→C→B，费用最低为3＋5＝8，所以铺设道路的最小费用为：6＋2＋8＝16。‎ 例10. （2012年陕西省理5分） 观察下列不等式 ‎[来源:学#科#网Z#X#X#K]‎ ‎，‎ ‎……‎ 照此规律，第五个不等式为 ▲ .‎ ‎【答案】。‎ ‎【考点】归纳规律。‎ ‎【解析】由题设中所给的三个不等式归纳出它们的共性：左边式子是连续正整数平方的倒数和，最后一个数的分母是不等式序号n+1的平方；右边分式中的分子与不等式序号n的关系是2n+1，分母是不等式的序号n+1，得出第n个不等式，即可得到通式：。‎ 令n=5，即可得出第五个不等式，即。‎ 例11. （2012年北京市文13分）设A是如下形式的2行3列的数表，‎ a b[来源:学_科_网Z_X_X_K]‎ c d e f 满足性质P：a，b，c，d，e，f∈[-1,1],且a+b+c+d+e+f=0。记ri（A）为A的第i行各数之和（i=1,2），c j（A）为A的第j列各数之和（j=1，2，3）；记k（A）为|r1(A)|, |r2(A)|, |c1(A)|，|c2(A)|，|c3(A)|中的最小值。‎ ‎（1）对如下数表A，求k（A）的值 ‎1‎ ‎1‎ ‎－0.8‎ ‎0.1‎ ‎－0.3‎ ‎－1‎ ‎（2）设数表A形如 ‎1‎ ‎1‎ ‎－1－2d d d ‎－1‎ 其中－1≤d≤0.求k（A）的最大值；‎ ‎（3）对所有满足性质P的2行3列的数表A ，求k(A)的最大值。‎ ‎【答案】解：（1）由题意可知，‎ ‎ ∴。‎ ‎（2）‎ ‎∵－1≤d≤0，‎ ‎∴。‎ ‎∴。‎ ‎∴当d=0时，k（A）取得最大值1。‎ ‎（3）任给满足性质P的数表A（如下所示）‎ a b c d e f 任意改变A三维行次序或列次序，或把A中的每个数换成它的相反数，所得数表A*仍满足性质P，并且k（A）=k（A*）‎ 因此，不防设r1（A）≥0，c1（A）≥0，c2（A）≥0，‎ 由k（A）的定义知，k（A）≤r1（A），k（A）≤c1（A），k（A）≤c2（A），‎ ‎∴‎ ‎∴k（A）≤1‎ 由（2）可知，存在满足性质P的数表A使k（A）=1，故k（A）的最大值为1。‎ ‎【考点】逻辑推理。‎ ‎【解析】（1）根据ri（A）为A的第i行各数之和（i=1，2），c j（A）为A的第j列各数之和（j=1，2，3）；求出|r1（A）|，|r2（A）|，|c1（A）|，|c2（A）|，|c3（A）|中的最小值可即为所求。‎ ‎（2）k（A）的定义可求出k（A）=1+d，然后根据d的取值范围可求出所求。‎ ‎（3）任意改变A三维行次序或列次序，或把A中的每个数换成它的相反数，所得数表A*仍满足性质P，并且k（A）=k（A*）。因此，不防设r1（A）≥0，c1（A）≥0，c2（A）≥0，然后利用不等式的性质可知3k（A）≤r1（A）+c1（A）+c2（A），从而求出k（A）的最大值。‎ 例12. （2012年上海市理18分）对于数集，其中，，定义向量集. 若对于任意，存在，使得，则称X具有性质P. 例如具有性质P.‎ ‎ （1）若＞2，且，求的值；（4分）‎ ‎ （2）若X具有性质P，求证：1ÎX，且当n＞1时，1=1；（6分）‎ ‎ （3）若X具有性质P，且1=1，（为常数），求有穷数列的通项公式.（8分）‎ ‎【答案】解：（1）选取，则Y中与垂直的元素必有形式。‎ ‎ ∴，从而=4。‎ ‎ （2）证明：取，设满足。‎ ‎ 由得，∴、异号。‎ ‎ ∵－1是X中唯一的负数，所以、中之一为－1，另一为1。‎ 故1ÎX。‎ 假设，其中，则。‎ 选取，并设满足，即。‎ 则、异号，从而、之中恰有一个为－1。‎ 若=－1，则，矛盾；‎ 若=－1，则，矛盾.‎ ‎∴=1。‎ ‎ （3）猜测，i=1, 2, …, 。‎ ‎ 记，=2, 3, …, 。‎ ‎ 先证明：若具有性质P，则也具有性质P。‎ ‎ 任取，、Î.当、中出现－1时，显然有满足。‎ ‎ 当且时，、≥1。‎ ‎ ∵具有性质P，∴有，、Î，使得。‎ 从而和中有一个是－1，不妨设=－1，‎ 假设Î且Ï，则。‎ 由，得，与Î矛盾。‎ ‎∴Î，从而也具有性质P。‎ 现用数学归纳法证明：，i=1, 2, …, 。‎ 当=2时，结论显然成立。‎ ‎ 假设时，有性质P，则，i=1, 2, …, ；‎ ‎ 则当时，若有性质P，则 ‎ 也有性质P，所以。‎ ‎ 取，并设满足，即。‎ 由此可得与中有且只有一个为－1。‎ ‎ 若，则，所以，这不可能；‎ ‎ ∴，，又，所以。‎ ‎ 综上所述，，i=1, 2, …, 。 ‎ ‎【考点】数集、集合的基本性质、元素与集合的关系，数学归纳法和反证法的应用。‎ ‎【解析】（1）根据题设直接求解。（2）用反证法给予证明。‎ ‎ （3）根据题设，先用反证法证明：若具有性质P，则也具有性质P，再用数学归纳法证明猜测，i=1, 2, …, 。‎ 例13. （2012年北京市理13分）设A是由m×n个实数组成的m行n列的数表，满足：每个数的绝对值不大于1，且所有数的和为零，记s(m，n)为所有这样的数表构成的集合。‎ 对于A∈S(m，n)，记Ri(A)为A的第ⅰ行各数之和（1≤ⅰ≤m），Cj(A)为A的第j列各数之和（1≤j≤n）；‎ 记K(A)为∣R1(A)∣,∣R2(A)∣,…,∣Rm(A)∣,∣C1(A)∣,∣C2(A)∣,…,∣Cn(A)∣中的最小值。‎ ‎（1）对如下数表A，求的值；‎ ‎1‎ ‎1‎ ‎－0.8‎ ‎0.1‎ ‎－0.3‎ ‎－1‎ ‎（2）设数表A∈S（2,3）形如 ‎1‎ ‎1‎ c a b ‎－1‎ 求的最大值；‎ ‎（3）给定正整数t，对于所有的A∈S（2，2t+1），求的最大值。‎ ‎【答案】‎ 解：（1）由题意可知，‎ ‎ ∴。‎ ‎（2）先用反证法证明：‎ 若，则，‎ ‎∴（无解）。‎ 同理可知。‎ ‎∴。‎ 由题设所有数和为0，即，‎ ‎∴，解得，与题设矛盾。‎ ‎∴。‎ 易知当时，存在。‎ ‎∴的最大值为1。‎ ‎（3）的最大值为。‎ 首先构造满足的：‎ ‎，‎ ‎。‎ 经计算知，中每个元素的绝对值都小于1，所有元素之和为0，且 ‎，，‎ ‎。‎ 下面证明是最大值。‎ 若不然，则存在一个数表A∈S（2，2t+1），使得。‎ 由的定义知的每一列两个数之和的绝对值都不小于，而两个绝对值不超过1的数的和，其绝对值不超过2，故的每一列两个数之和的绝对值都在区间中. 由于，故的每一列两个数符号均与列和的符号相同，且绝对值均不小于。‎ 设中有列的列和为正，有列的列和为负，由对称性不妨设，则。另外，由对称性不妨设的第一行行和为正，第二行行和为负。‎ 考虑的第一行，由前面结论知的第一行有不超过个正数和不少于个负数，每个正数的绝对值不超过1（即每个正数均不超过1），每个负数的绝对值不小于（即每个负数均不超过）。‎ 因此，故的第一行行和的绝对值小于，与假设矛盾。‎ 因此的最大值为。‎ ‎【考点】逻辑推理，反证法的应用。‎ ‎【解析】（1）根据ri（A）为A的第i行各数之和（i=1，2），c j（A）为A的第j列各数之和（j=1，2，3）；求出|r1（A）|，|r2（A）|，|c1（A）|，|c2（A）|，|c3（A）|中的最小值可即为所求。‎ ‎ （2）用反证法证明。‎ ‎ （3）先构造满足的，用反证法证明是最大值。[来源:学科网]‎ 例14. （2012年湖北省理14分）（Ⅰ）已知函数，其中为有理数，且.求的最小值；‎ ‎（II）试用（1）的结果证明如下命题：设为正有理数，若，则；‎ ‎（III）请将（2）中的命题推广到一般形式，并用数学归纳法证明你所推广的命题。注：当为正有理数时，有求导公式 ‎【答案】解：（Ⅰ），令，解得。‎ 当时，，所以在内是减函数；‎ 当 时，，所以在内是增函数。‎ ‎∴函数在处取得最小值。 ‎ ‎（Ⅱ）由（Ⅰ）知，当时，有，即 ①。‎ 若，中有一个为0，则成立；‎ 若，均不为0，又，可得。‎ 于是在①中令，，可得，‎ 即，亦即。‎ 综上，对，，为正有理数且，总有 ②。‎ ‎（Ⅲ）（Ⅱ）中命题的推广形式为：‎ 设为非负实数，为正有理数. ‎ 若，则. ③ ‎ 用数学归纳法证明如下：‎ ‎（1）当时，，有，③成立。‎ ‎（2）假设当时，③成立，即若为非负实数，为正有理数，‎ 且，则。 ‎ 当时，已知为非负实数，为正有理数，‎ 且，此时，即。‎ ‎∴=。‎ ‎∵，由归纳假设可得 ‎，‎ ‎∴。‎ 又∵，由②得 ‎，‎ ‎∴.‎ 故当时，③成立。‎ 由（1）（2）可知，对一切正整数，所推广的命题成立，‎ ‎【考点】利用导数求函数的最值，数学归纳法的应用。‎ ‎【解析】（Ⅰ）应用导数求函数的最值。‎ ‎　　　　（Ⅱ）由（Ⅰ）的结论，分，中有一个为0和，均不为0讨论即可。‎ ‎　　　　（Ⅲ）应用数学归纳法证明。‎