江西专版2020中考数学复习方案第七单元图形的变化第27课时轴对称与中心对称课件

江西专版2020中考数学复习方案第七单元图形的变化第27课时轴对称与中心对称课件

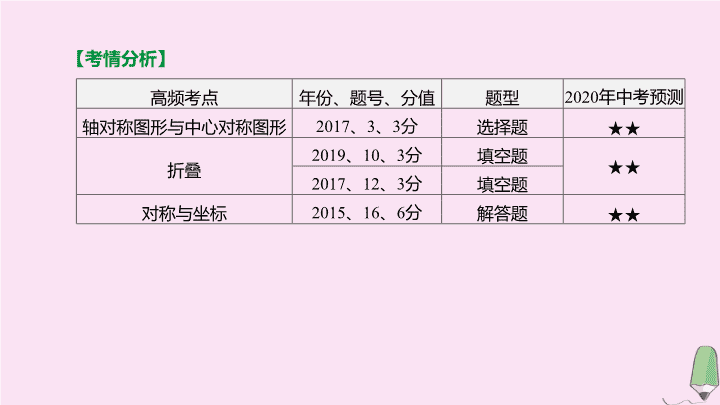
单元思维导图 第 27 课时 轴对称与中心对称 第七单元　图形的变化 【 考情分析 】 高频考点 年份、题号、分值 题型 2020 年中考预测 轴对称图形 与中心对称 图形 2017 、 3 、 3 分 选择题 ★★ 折叠 2019 、 10 、 3 分 填空题 ★★ 2017 、 12 、 3 分 填空题 对称与坐标 2015 、 16 、 6 分 解答题 ★★ 考点一　轴对称与中心对称 考点聚焦 轴对称 中心对称 图形 性质 (1) 成轴对称的两个图形是全等图形 ; (2) 成轴对称的两个图形只有一条对称轴 ; (3) 对应点连线被对称轴 ① 　 　   (1) 成中心对称的两个图形是全等图形 ; (2) 成中心对称的两个图形只有一个对称中心 ; (3) 对应点连线交于对称中心 , 并且被对称中心 ② 　　   垂直平分 平分 ( 续表 ) 轴对称 中心对称 作图 方法 (1) 找出原图形的关键点 , 作出它们关于对称轴 ( 或对称中心 ) 的对称点 ; (2) 根据原图形依次连接各对称点即可 考点二　轴对称图形与中心对称图形 轴对称图形 中心对称图形 图形 判断 方法 (1) 有对称轴 —— 直线 ; (2) 图形沿对称轴折叠后完全重合 (1) 有对称中心 —— 点 ; (2) 图形绕对称中心旋转 ③ 　　　　 后完全重合   180° 【 温馨提示 】 常见的轴对称图形、中心对称图形 考点三　图形的折叠及最短路径问题 1 . 图形的折叠 (1) 位于折痕两侧的图形关于折痕 ④ 　 　　　 ;  (2) 折叠前后的两部分图形全等 , 对应边、角、线段、周长、面积等均相等 ; (3) 折叠前后 , 对应点的连线被折痕所在直线垂直平分 . 成轴对称 2 . 求最短路径问题 (1) 基本问题 : 如图 27-1 ① , 在直线 l 上找一点 P , 使得点 P 到点 A 和点 B 的距离之和最短 , 即 PA + PB 的值最小 . (2) 具体作法 : 如图 27-1 ② , 作点 A 关于直线 l 的对称点 A' , 连接 A'B 与直线 l 相交于点 P , 连接 PA , PB , 则点 P 即为所求 , 此时 PA + PB 的值最小 . 图 27-1 题组一　必会题 对点演练 1 . [2019· 泰州 ] 下列图形中的轴对称图形是 ( 　　 ) B 图 27-2 2 . [2019· 杭州 ] 在平面直角坐标系中 , 点 A ( m ,2) 与点 B (3, n ) 关于 y 轴对称 , 则 ( 　　 ) A .m= 3, n= 2 B .m= -3, n= 2 C .m= 2, n= 2 D .m= -2, n= -3 B 3 . 如图 27-3, 直线 l 是四边形 ABCD 的对称轴 , 有下面四个结论 : ① AB=AD ; ② BO= DO ; ③ BD ⊥ AC ; ④ △ ABC ≌△ ADC. 其中正确的结论是 　 　　　 . ( 填序号 )  ①②③④ 图 27-3 4 . [2019· 甘肃 ] 如图 27-4, 在矩形 ABCD 中 , AB= 10, AD= 6, E 为 BC 上一点 , 把 △ CDE 沿 DE 折叠 , 使点 C 落在 AB 边上的 F 处 , 则 CE 的长为 　　　　 .  图 27-4 题组二　易错题 【 失分点 】 轴对称图形找不全 , 不明白折叠的实质是轴对称导致错误 ; 不能利用轴对称解决最短路线问题 . 5 . 如图 27-5, 在 3×3 的正方形网格中 , 以格点为顶点的三角形称为格点三角形 , 在图中画出与 △ ABC 关于某条直线对称的格点三角形 , 最多能画 ( 　　 ) A . 5 个 B . 6 个 C . 7 个 D . 8 个 图 27-5 [ 答案 ] B 　 [ 解析 ] 如图 , 最多能画出 6 个格点三角形与 △ ABC 成轴对称 . 故选 B . 6 . 如图 27-6, 点 P 是边长为 1 的菱形 ABCD 对角线 AC 上的一个动点 , 点 M , N 分别是 AB , BC 边的中点 , 则 MP + PN 的最小值是 　　　　 .  图 27-6 [ 答案 ] 1 　 [ 解析 ] 如图 , 取 AD 的中点 M' , 连接 M'N 交 AC 于点 P , 则由菱形的轴对称性可知 M , M' 关于直线 AC 对称 , 从而 PM'=PM , 此时 MP + PN 的值最小 , 而易知四边形 CDM'N 是平行四边形 , 故 M'N=CD= 1, 于是 , MP + PN 的最小值是 1 . 考向一　识别对称图形 例 1 [2019· 烟台 ] 下列智能手机的功能图标中 , 既是轴对称图形又是中心对称图形的是 ( 　　 ) 图 27-7 C 【 方法点析 】 (1) 识别轴对称图形的方法 : 把一个图形沿着一条直线翻折 , 如果直线两旁的部分能够完全重合 , 那么这个图形就是轴对称图形 . (2) 识别中心对称图形的方法 : 把一个图形绕某一点旋转 180 °, 如果旋转后的图形能够与自身重合 , 那么这个图形就是中心对称图形 . | 考向精练 | 1 . [2017· 江西 3 题 ] 下列图形 , 是轴对称图形的是 ( 　　 ) 图 27-8 [ 答案 ] C 　 [ 解析 ]A,B,D 三个选项中的图形均无法沿着某一条直线折叠 , 使直线两旁的部分能互相重合 , 只有 C 选项沿着图中的某一条直线折叠 , 直线两旁的部分能够互相重合 . 故选 C . 2 . [2019· 兰州 ] 剪纸是中国特有的民间艺术 , 在如图 27-9 所示的四个剪纸图案中 , 既是轴对称又是中心对称图形的是 ( 　　 ) C 图 27-9 3 . [2019· 泰安 ] 下列图形 : 图 27-10 其中 , 是轴对称图形且有两条对称轴的是 ( 　　 ) A . ①② B . ②③ C . ②④ D . ③④ [ 答案 ] A 　 [ 解析 ] 四个图形中 , 轴对称图形有 : ①②③ , 其中图①有 2 条对称轴 , 图②有 2 条对称轴 , 图③有 4 条对称轴 . 故选 A . 考向二　与图形对称相关的计算 B | 考向精练 | 1 . 在平面直角坐标系中 , 已知点 A (-4,3) 与点 B 关于原点对称 , 则点 B 的坐标为 ( 　　 ) A . (-4,-3) B . (4,3) C . (4,-3) D . (-4,3) C 2 . [2015· 江西 16 题 ] 如图 27-11, 正方形 ABCD 与正方形 A 1 B 1 C 1 D 1 关于某点中心对称 . 已知 A , D 1 , D 三点的坐标分别是 (0,4),(0,3),(0,2) . (1) 求对称中心的坐标 ; (2) 写出顶点 B , C , B 1 , C 1 的坐标 . 图 27-11 考向三　与图形折叠有关的计算 例 3 [2018· 遵义 ] 如图 27-12, 在菱形 ABCD 中 , ∠ ABC= 120°, 将菱形折叠 , 使点 A 恰好落在对角线 BD 上的点 G 处 ( 不与 B , D 重合 ), 折痕为 EF , 若 DG= 2, BG= 6, 则 BE 的长为 　　　　 .  图 27-12 [ 答案 ] 2.8 【 方法点析 】 解决折叠问题的关键 : 一是折痕两边的折叠部分是全等的 ; 二是折叠过程中对应点的连线被折痕垂直平分 . | 考向精练 | 1 . [2019· 吉林 ] 如图 27-13, 在四边形 ABCD 中 , AB= 10, BD ⊥ AD , 若将 △ BCD 沿 BD 折叠 , 点 C 与边 AB 的中点 E 恰好重合 , 则四边形 BCDE 的周长为 　　　　 .  图 27-13 [ 答案 ] 20 2 . [2019· 烟台 ] 小明将一张正方形纸片按如图 27-14 所示的顺序折叠成纸飞机 , 当机翼展开在同一平面时 ( 机翼间无缝隙 ), ∠ AOB 的度数是 　　　　 .  图 27-14 22.5°