- 2021-04-13 发布 |
- 37.5 KB |
- 3页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
二次函数与一元二次方程教案2
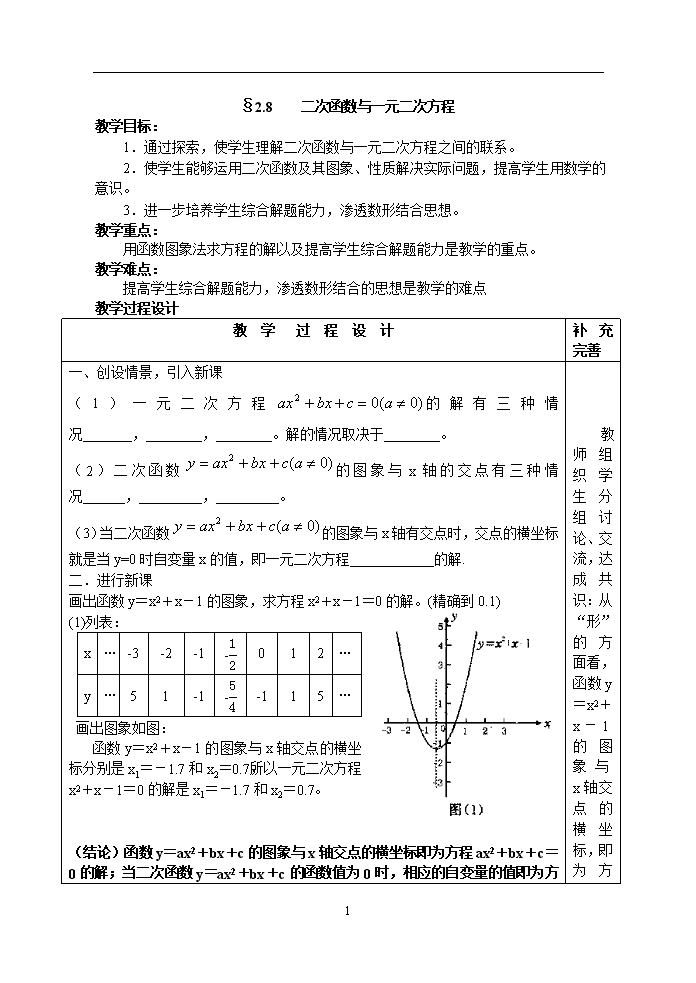
§2.8 二次函数与一元二次方程 教学目标: 1.通过探索,使学生理解二次函数与一元二次方程之间的联系。 2.使学生能够运用二次函数及其图象、性质解决实际问题,提高学生用数学的意识。 3.进一步培养学生综合解题能力,渗透数形结合思想。 教学重点: 用函数图象法求方程的解以及提高学生综合解题能力是教学的重点。 教学难点: 提高学生综合解题能力,渗透数形结合的思想是教学的难点 教学过程设计 教 学 过 程 设 计 补充完善 一、创设情景,引入新课 (1)一元二次方程的解有三种情况 , , 。解的情况取决于 。 (2)二次函数的图象与x轴的交点有三种情况 , , 。 (3)当二次函数的图象与x轴有交点时,交点的横坐标就是当y=0时自变量x的值,即一元二次方程 的解. 二.进行新课 画出函数y=x2+x-1的图象,求方程x2+x-1=0的解。(精确到0.1) (1)列表: x … -3 -2 -1 - 0 1 2 … y … 5 1 -1 - -1 1 5 … 画出图象如图: 函数y=x2+x-1的图象与x轴交点的横坐标分别是x1=-1.7和x2=0.7,所以一元二次方程x2+x-1=0的解是x1=-1.7和x2=0.7。 (结论)函数y=ax2+bx+c的图象与x轴交点的横坐标即为方程ax2+bx+c=0的解;当二次函数y=ax2 教师组织学生分组讨论、交流,达成共识:从“形”的方面看,函数y=x2 3 +bx+c的函数值为0时,相应的自变量的值即为方程ax2+bx+c=0的解,这一结论反映了二次函数与一元二次方程的关系。 三、典例分析 例1。把一个小球以20m/s的速度竖直向上弹出,它在空中的高度h(m)与时间t(s)满足关系:.当时,小球的运动时间为( ) A.20s B.2s C.()s D.()s 例2.已知方程()的两个根为和,那么可知抛物线(a≠0)的对称轴为 。 分析: 例3.已知二次函数的图象和x轴有交点,则k的取值范围是( ) A. B.且k≠0 C. D.且k≠0 分析:函数的交点与方程的解用△联系起来。 随堂练习: 1、方程的根为 , .二次函数与x轴的交点是 . 2、抛物线的一部分如图1所示,该抛物 线在y轴右侧部分与x轴交点的坐标是( ) A.(,0) B.(1,0) C.(2,0) D.(3,0) 3、若一元二次方程有两个实数根,则抛物线与x轴( ) A.有两个交点 B.只有一个交点 C.至少有一个交点 D.至多有一个交点 归纳小结 (结论)函数y=ax2+bx+c的图象与x轴交点的横坐标即为方程ax2+bx+c=0的解;当二次函数y=ax2 +x-1的图象与x轴交点的横坐标,即为方程x2+x-1=0的解;从“数”的方面看,当二次函数y=x2+x-1的函数值为0时,相应的自变量的值即为方程x2+x-1=0的解。 3 +bx+c的函数值为0时,相应的自变量的值即为方程ax2+bx+c=0的解,这一结论反映了二次函数与一元二次方程的关系。 四、知识延伸: 1、关于x的一元二次方程没有实数根,则抛物线的顶点在( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限 2、不论自变量x取什么实数,二次函数的值总是正值,你认为m的取值范围是 ,此时关于x的一元二次方程的根的情况是 (填“有实根”或“无实根”). 3、函数的图象如图3所示,那么关于x的一元二次方程的根的情况是( ) A.有两个不相等的实数根 B.有两个异号的实数根 C.有两个相等的实数根 D.没有实数根 4.已知二次函数. (1)说明抛物线与x轴有两个不同交点; (2)求这两个交点间的距离(关于a的表达式); (3)a取何值时,两点间的距离最小? 五、课堂检测 1、(2005 温州课改)若二次函数的图象与轴没有交点,其中为整数,则 .(只要求写出一个). 2、(2005 成都课改)已知二次函数的图象与轴的一个交点为,那么该二次函数图象的顶点坐标为 . 3、抛物线与x轴有 个交点. 3查看更多