第16课 特殊三角形中考复习

第16课 特殊三角形中考复习

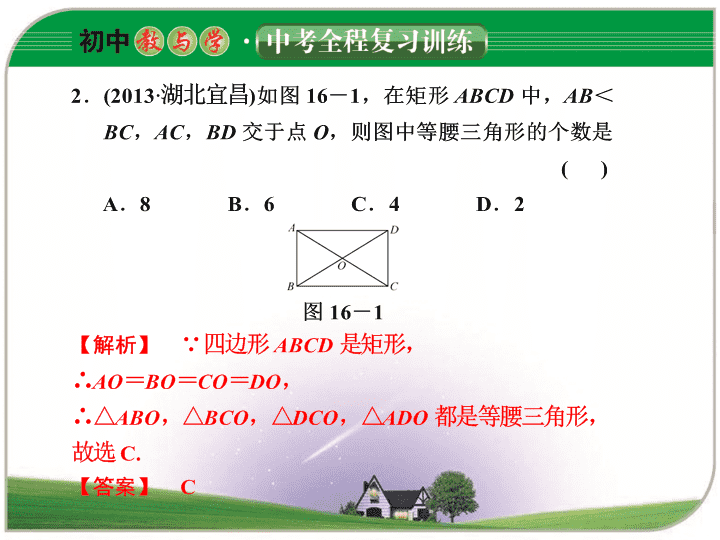
1．(2013·江苏徐州)若等腰三角形的顶角为 80°，则它的底 角度数为 ( ) A．80° B．50° C．40° D．20° 【解析】 ∵等腰三角形的顶角为 80°， ∴它的底角度数为1 2(180°－80°)＝50°. 【答案】 B 2．(2013·湖北宜昌)如图 16－1，在矩形 ABCD 中，AB＜ BC，AC，BD 交于点 O，则图中等腰三角形的个数是 ( ) A．8 B．6 C．4 D．2 图 16－1 【解析】 ∵四边形 ABCD 是矩形， ∴AO＝BO＝CO＝DO， ∴△ABO，△BCO，△DCO，△ADO 都是等腰三角形， 故选 C. 【答案】 C 3．(2013·广东佛山)如图 16－2，若∠A＝ 60°，AC＝20 m，则 BC 大约是(结果精 确到 0.1 m) ( ) A．34.64 m B．34.6 m C．28.3 m D．17.3 m 【解析】 ∵∠A＝60°，∠C＝90°， ∴∠B＝30°，∴AB＝2AC. ∵AC＝20 m，∴AB＝40 m， ∴BC＝ AB2－AC2＝20 3≈34.6(m)． 【答案】 B 4．(2013·浙江衢州)将一个有45°角的三角尺的直角顶点放在一张宽为3 cm 的纸带边沿上．另一个顶点在纸带的另一边沿上，测得三角尺的一边 与纸带的一边所在的直线成 30°角，如图 16－3，则三角尺的最大边的 长为 ( ) A．3 cm B．6 cm C．3 2 cm D．6 2 cm 图 16－3 【解析】 如解图 1，过点 C 作 CD⊥AD，则 CD＝3. 在 Rt△ADC 中，∵∠CAD＝30°，∴AC＝2CD＝2×3＝6. ∵三角尺是有 45°角的三角尺， ∴AB＝AC＝6， ∴BC＝ AB2＋AC2＝ 62＋62＝ 72＝6 2. (解图 1)【答案】 D 5．(2012·四川凉山)如图 16－4，一个等边三角形纸片，剪 去一个角后得到一个四边形，则图中∠α＋∠β的度数 是 ( ) A．180° B．220° C．240° D．300° 图 16－4 【解析】 ∵等边三角形的每个角都为 60°， ∴两底角的和＝60°＋60°＝120°， ∴∠α＋∠β＝360°－120°＝240°. 【答案】 C 考点一　等腰三角形的有关概念 　　　　　　　　　 　　　　　　　　 1．有两边相等的三角形叫做等腰三角形，相等的边叫腰， 另一边叫底边，两腰夹角叫顶角，腰和底边夹角叫底 角． 2．三角形按角分类可分成锐角三角形，直角三角形，钝 角三角形． 考点点拨 1．等腰三角形的边(腰与底)或角(顶角与底角)不确定时往 往要分类讨论． 2．计算角度时，常用方程思想，结合三角形内角和为 180° 来解． 【精选考题 1】 (2013·新疆)等腰三角形的两边长分别为 3 和 6，则 这个等腰三角形的周长为 ( ) A．12 B．15 C．12 或 15 D．18 点评：(1)本题考查等腰三角形的性质和三角形的三边关系，难度中 等． (2)已知条件中没有明确等腰三角形的边是腰还是底边时，一定要想 到两种情况，进行分类讨论，还应验证各种情况是否能构成三角形， 验证非常重要，也是解题的关键． 解析：∵已知长度为 3 和 6 的两边，没有明确是底边还是腰，∴有 两种情况，需要分类讨论． ①当 3 为底时，另外两边都为 6， 3，6，6 可以构成三角形，周长为 15. ②当 3 为腰时，另外两边为 3 和 6， ∵3＋3＝6，∴不能构成三角形，故舍去． ∴答案只有 15.故选 B. 答案：B 【预测演练 1】 如图 16－5，在△ABC 中，AB＝AC， 点 D 在 AC 边上，且 BD＝BC＝AD，则图中的等腰三 角形的个数为 ( ) A．0 B．1 C．2 D．3 图 16－5 解析：△ABC，△ABD，△BCD 均为等腰三角形，共 3 个． 答案：D 考点二　等腰三角形的性质与判定 　　　　　　　　　 　　　　　　　　1．等腰三角形的性质： (1)等腰三角形的两个底角相等，简称为等边对等角； (2)等腰三角形的顶角平分线，底边上的中线，底边上 的高互相重合，简称为三线合一． 2．等腰三角形的判定：如果一个三角形有两个角相等， 那么这两个角所对的边也相等，简称为等角对等边． 考点点拨 1．等腰三角形的性质常用于证明角相等、线段相等、直线垂 直等，其用途较广，题型变化多． 2．已知等腰三角形，常添的辅助线是作底边上的高(或顶角平 分线或底边上的中线)；角平分线＋平行线等腰三角形． 3．等腰三角形是轴对称图形，对称轴是底边的垂直平分线． 4．应用性质“三线合一”时，一定要注意是顶角的平分线， 底边上的中线，底边上的高互相重合，利用它可以证明线 段相等，角相等及直线垂直；“等边对等角”或“等角对 等边”仅限于在同一个三角形中，在两个三角形中若两边 相等，则它们所对的角不一定相等． 【精选考题 2】 (2013·浙江杭州)如图 16－6，在等腰梯形 ABCD 中，AB∥DC，线段 AG，BG 分别交 CD 于点 E， F，DE＝CF.求证：△GAB 是等腰三角形． 点评：(1)本题主要考查等腰三角形的判定，等腰梯形的性质以及全等三角 形的判定与性质，难度中等． (2)利用△ADE≌△BCF 证∠GAB＝∠GBA 是解决本题的关键． (3)注意数形结合思想的应用． 解析：∵在等腰梯形 ABCD 中，AB∥DC， ∴AD＝BC，∠D＝∠C，∠DAB＝∠CBA. 在△ADE 和△BCF 中，∵ AD＝BC， ∠D＝∠C， DE＝CF， ∴△ADE≌△BCF(SAS)，∴∠DAE＝∠CBF. ∵∠DAB＝∠CBA，∴∠GAB＝∠GBA， ∴GA＝GB，即△GAB 为等腰三角形． 【预测演练 2】 如图 16－7，在等腰△ABC 中，CH 是底边 上的高，点 P 是线段 CH 上不与端点重合的任意一点，连 结 AP 并延长交 BC 于点 E，连结 BP 并延长交 AC 于点 F. (1)求证：∠CAE＝∠CBF； (2)求证：AE＝BF； (3)以线段 AE，BF 和 AB 为边构成一个新的三角形 ABG(点 E 与点 F 重合于点 G)，记△ABC 和△ABG 的面积分别 为 S△ABC 和 S△ABG，如果存在点 P，能使 S△ABC＝S△ABG， 求∠C 的取值范围． 图 16－7 解析：(1)∵△ABC 是等腰三角形，CH 是底边上的高线， ∴AC＝BC，∠ACP＝∠BCP. 又∵CP＝CP，∴△ACP≌△BCP，∴∠CAP＝∠CBP，即∠CAE＝∠CBF. (2)∵∠ACE＝∠BCF，∠CAE＝∠CBF，AC＝BC， ∴△ACE≌△BCF，∴AE＝BF. (3)由(2)知△ABG 是以 AB 为底边的等腰三角形， ∴S△ABC＝S△ABG 等价于 AE＝AC. ①当∠C 为直角或钝角时，在△ACE 中，无论点 P 在 CH 上何处，均有 AE＞AC，∴结论 不成立； ②当∠C 为锐角时，∠A＝90°－1 2 ∠C， 而∠CAE＜∠A，要使 AE＝AC，只需∠C＝∠CEA，此时，∠CAE＝180°－2∠C，即只 需 180°－2∠C＜90°－1 2 ∠C，解得 60°＜∠C＜90°. 考点三　等边三角形的性质与判定 　　　　　　　　　 　　　　　　　　1．三边都相等的三角形叫做等边三角形． 2．等边三角形的三个内角相等，即每一个内角都等于 60°． 3．等边三角形的判定： (1)三个角都相等的三角形是等边三角形； (2)有一个角是 60°的等腰三角形是等边三角形． 考点点拨 1．等边三角形具有等腰三角形的所有性质，它的性质常 用于计算角度，再结合 30°，90°，120°等特殊角能得 到三角形边之间的关系． 2．判定等边三角形可以先从判定等腰三角形入手，再寻 找一个 60°角，或直接找两个 60°角，那么第三个角也 是 60°. 3．等边三角形是轴对称图形，但不是中心对称图形． 【精选考题 3】 (2013·山东菏泽)我们规定：将一个平面 图形分成面积相等的两部分的直线叫做该平面图形的 “面线”，“面线”被这个平面图形截得的线段叫做该 图形的“面径”(例如圆的直径就是它的“面径”)．已 知等边三角形的边长为 2，则它的“面径”长可以是 (写出一个即可)． 点评：(1)本题主要考查等边三角形的性质，难度中等． (2)读懂题意，弄清“面径”的定义，并准确判断出等边三角 形的最短与最长的面径是解决本题的关键． 解析：如解图 2， 由图易知等边三角形的高 AD 是最长的面径，AD＝2× 3 2 ＝ 3. 当 EF∥BC 且 S△AEF S△ABC ＝1 2 时，EF 为最短面径， ∴EF2 BC2＝1 2 ，∴EF＝ 2. ∴它的“面径”长可以是 2， 3(或介于 2和 3之间的任意一个实数)． 答案：2， 3(或介于 2和 3之间的任意一个实数) 【预测演练 3】 (1)如图 16－8，在正方形 ABCD 中，M 是 BC 边上(不 含端点 B，C)任意一点，P 是 BC 延长线上一点，N 是∠DCP 平分线 上的一点．若∠AMN＝90°，求证：AM＝MN. 证明：在边 AB 上截取 AE＝MC，连结 ME.在正方形 ABCD 中，∠B ＝∠BCD＝90°，AB＝BC.∴∠NMC＝180°－∠AMN－∠AMB＝180° －∠B－∠AMB＝∠MAB＝∠MAE. 下面请你完成余下的证明过程； (2)若将题中的“正方形 ABCD”改为“正三角形 ABC”(如图 16－9)， N 是∠ACP 的平分线上一点，则当∠AMN＝60°时，结论 AM＝MN 是否还成立？请说明理由； (3)若将上题中的“正方形 ABCD”改为“正 n 边形 ABCD…X”，请你 作出猜想：当∠AMN＝________度时，结论 AM＝MN 仍然成立(直 接写出答案，不需要证明)． 解析：(1)∵AE＝MC，∴BE＝BM，∴∠BEM＝∠EMB＝45°，∴∠AEM＝135°. ∵CN 平分∠DCP，∴∠PCN＝45°，∴∠MCN＝135°＝∠AEM. 在△AEM 和△MCN 中，∵ ∠AEM＝∠MCN， AE＝MC， ∠MAE＝∠NMC， ∴△AEM≌△MCN(ASA)，∴AM＝MN. (2)结论 AM＝MN 仍然成立．理由如下： 在 AB 上截取 BD＝BM，连结 DM，如解图 3. ∵△ABC 是正三角形，∴AB＝BC，∠B＝60°. ∵BD＝BM，∴AD＝MC，△BDM 是等边三角形， ∴∠BMD＝∠AMN＝60°＝∠NCP， ∴∠ADM＝∠MCN＝120°，∠AMD＋∠NMC＝∠N＋∠NMC＝60°，∴∠AMD＝∠N， ∴△AMD≌△MNC(AAS)，∴AM＝MN. (3)180（n－2） n . 考点四　直角三角形的性质与判定 　　　　　　　　　 　　　　　　　　1．有一个角是直角的三角形叫做直角三角形，两条直角边相等的三 角形叫做等腰直角三角形． 2．直角三角形的性质： (1)直角三角形中两个锐角互余； (2)直角三角形斜边上的中线等于斜边的一半； (3)直角三角形 30°角所对的直角边等于斜边的一半． 3．直角三角形的判定： (1)有一个角是直角的三角形是直角三角形； (2)有两个角互余的三角形是直角三角形； (3)如果三角形一条边上的中线等于这条边的一半，那么这个三 角形是直角三角形． 考点点拨 1．“直角三角形中两锐角互余”这一性质常用来计算角 度，或与同角(或等角)的余角(或补角)相等相结合证明 角相等，常用于矩形、正方形的有关证明中． 2．直角三角形中，30°角所对的直角边是斜边的一半．该 定理描述的是特殊角与直角三角形边的关系，常用于 证明线段之间的一半数量关系，也经常用于计算线段 的长度，但该定理只适用于直角三角形． 3．直角三角形斜边上的中线等于斜边的一半．这个性质 定理常用于证明两线段的一半数量关系，注意直角三 角形这一前提不能漏． 【精选考题 4】 (2013·台湾)如图 16－10，△ABC 中，D 为 AB 的中点， E 在 AC 上，且 BE⊥AC.若 DE＝10，AE＝16，则 BE 的长度为( ) A．10 B．11 C．12 D．13 图 16－10 点评：(1)本题考查直角三角形的性质和勾股定理的运用，难度中等． (2)直角三角形中，斜边上的中线等于斜边的一半． 解析：∵BE⊥AC，∴△AEB 是直角三角形． ∵D 为 AB 的中点，DE＝10，∴AB＝20. ∵AE＝16，∴BE＝ AB2－AE2＝12.故选 C. 答案：C 【预测演练 4】 在△ABC 中，∠ABC＝90°，点 E 在直线 AB 上，ED 与直线 AC 垂直， 垂足为 D，且点 M 为 EC 中点，连结 BM，DM. (1)如图 16－11①，点 E 在线段 AB 上，探究线段 BM 与 DM 及∠BMD 与∠BCD 所满 足的数量关系，请你写出所得结论并给予证明； 图 16－11 (2)如图 16－11②，若点 E 在 BA 的延长线上，你在(1)中得到的结论是否发生变化？ (3)若点 E 在 AB 的延长线上，请你根据条件画出相应的图形，并直接写出线段 BM 与 DM 及∠BMD 与∠BCD 所满足的数量关系． 解析：(1)结论：BM＝DM，∠BMD＝2∠BCD. ∵BM，DM 分别是 Rt△EBC，Rt△EDC 的斜边上的中线， ∴BM＝DM＝1 2CE，即 BM＝MC＝DM. ∴∠MCB＝∠MBC，即∠BME＝2∠BCM. 同理：∠DME＝2∠DCM. ∴∠BMD＝∠BME＋∠DME＝2(∠BCM＋∠DCM)＝2∠BCD. (2)在(1)中得到的结论仍然成立，即 BM＝DM，∠BMD＝2∠BCD.理由如下： ∵点 M 是 Rt△EBC 和 Rt△EDC 的斜边中点，∴BM＝1 2EC＝DM，即 DM＝BM＝MC. ∴∠MBC＝∠MCB，∠MDC＝∠MCD.∴∠BME＝2∠BCM，∠DME＝2∠DCM. ∴∠BMD＝∠BME－∠DME＝2(∠BCM－∠DCM)＝2∠BCD. (3)所画图形如解图 4 所示： (解图 4) 解图 4①中有 BM＝DM，∠BMD＝2∠BCD. 解图 4②中∠BCD 不存在，有 BM＝DM. 解图 4③中有 BM＝DM，∠BMD＝360°－2∠BCD. 考点五　直角三角形的面积与勾股定理 　　　　　　　　　 　　　　　　　　1．勾股定理：直角三角形中两直角边的平方和等于斜边 的平方． 2．勾股定理的逆定理：如果三角形的三边长 a，b，c(c 最 大)满足 a2＋b2＝c2，那么这个三角形是直角三角形． 考点点拨 1．若直角三角形三边为 a，b，c(c 为斜边)，斜边上的高 为 h，则 S△＝1 2ab＝1 2ch，由此可得斜边上的高 h＝ab c . 利用等积法常可以求解斜边上的高． 2．计算三角形面积时，常利用中线，等分点等进行面积 转化． 3．利用直角三角形的性质和判定，尤其是勾股定理及其 逆定理，能够解决三角形或四边形或圆中的一些问题． 【中考真题 5】 (2013·四川资阳)如图 16－12，点 E 在正方形 ABCD 内， 满足∠AEB＝90°，AE＝6，BE＝8，则阴影部分的面积是 ( ) A．48 B．60 C．76 D．80 图 16－12 点评：(1)本题主要考查勾股定理的运用及正方形的性质． (2)解决本题的关键是判断△ABE 为直角三角形，运用勾股定理及面积公 式求解． 解析：∵∠AEB＝90°，AE＝6，BE＝8， ∴在 Rt△ABE 中，AB2＝AE2＋BE2＝100， ∴S 阴影部分＝S 正方形 ABCD－S△ABE＝AB2－1 2AE·BE＝100－1 2 ×6×8＝76. 答案：C 【预测演练 5】 如图 16－13，台风中心位于点 P，并沿东北方向 PQ 移动，已知台风移动的速度为 30 km/h，受影响区域的半径为 200 km，B 市位于点 P 的北偏东 75°方向上，距离 P 点 320 km 处． (1)说明本次台风会影响 B 市； (2)求这次台风影响 B 市的时间． 解析：(1)作 BH⊥PQ 于点 H，如解图 5. 由条件知，PB＝320，∠BPQ＝30°，∴BH＝1 2PB＝160＜200， ∴本次台风会影响 B 市． (2)设台风中心移动到 P1 处时，台风开始影响 B 市，台风中心移 动到 P2 处时，台风影响结束． 由(1)得 BH＝160，由条件得 BP1＝BP2＝200， ∴P1P2＝2 2002－1602＝240(km)． ∴台风影响 B 市的时间 t＝240 30 ＝8(h)． 1.在利用勾股定理时，一定要看清题中所给的条件是不是直角三角 形，所给的边是直角边还是斜边，如果题中未说明是直角边还 是斜边，则需要分类讨论． 2．用面积法证题是常用的技巧方法之一，使用这种方法时一般是 利用某个图形的多种面积求法或面积之间的和差关系列出等 式，从而得到要证明的结论． 3．在直角三角形中，斜边上的中线等于斜边的一半，同时这条中 线将直角三角形分成了两个等腰三角形，这一特征在解题中时 有运用；当图中无直角时，可通过添加辅助线来构造直角三角 形，若图中有特殊角，如 30°，45°，60°的角，在作辅助线 时，要注意保持其完整性，以便应用特殊三角形的性质． 4．等边三角形是等腰三角形，但等腰三角形不一定是等边三 角形，等边三角形拥有等腰三角形的所有性质，但不分顶 角、底角，因为等边三角形的任何一个角都为 60°，任何一 条边都相等． 5．解答等腰三角形的有关问题时，常作辅助线，构造出“三 线合一”的基本图形，在添加辅助线时，要根据具体情况 而定，表达辅助线的语句不能限制太多，如“作一边上的 高并且要平分这条边”，“作一个角的平分线并且垂直对 边”等，这些都是不正确的． 6．在解有关等腰三角形的问题时，不要总认为腰大于底，实 际上底也可以大于腰，此时也能构成三角形． 7．在等腰三角形中，若条件中没有明确底和腰时，一般应从 某一边是底还是腰这两个方面进行讨论，还要特别注意构 成三角形的条件；同样，在条件中没有明确底角和顶角时， 也要进行分类讨论，将问题考虑全面，不能漏解． 8．在已知三角形三边的前提下，判断这个三角形是否为直角 三角形，首先要确定三条边中的最大边，再根据勾股定理 的逆定理来判定．在解题时，往往受思维定式的影响，误 认为如果是直角三角形，则 c 就是斜边，从而造成误解． 1．(2012·贵州铜仁)如图 16－14，在△ABC 中，∠ABC 和∠ACB 的平分 线交于点 E，过点 E 作 MN∥BC 交 AB 于点 M，交 AC 于点 N.若 BM ＋CN＝9，则线段 MN 的长为 ( ) A．6 B．7 C．8 D．9 图 16－14 点评：(1)本题考查平行线的性质与等腰三角形的判定，难度中等． (2)求解本题的关键是把 MN 转化为 BM＋CN. 解析：提示：由已知易得△BME 与△CNE 为等腰三角形，则可得 MN＝ BM＋CN＝9. 答案：D 2．(2013·浙江绍兴)如图 16－15 钢架中，焊上等长的 13 根钢条来加固钢架，若 AP1＝P1P2 ＝P2P3＝…＝P13P14＝P14A，则∠A 的度数是 ． 图 16－15 点评：(1)本题主要考查等腰三角形的性质和三角形外角的性质，难度较大． (2)解决本题的关键是熟练运用等边对等角及三角形的一个外角等于与它不相邻的两个内 角的和． 解析：设∠A＝x，∵AP1＝P1P2＝P2P3＝…＝P13P14＝P14A，∴∠A＝∠AP2P1＝∠AP13P14 ＝x，∴∠P2P1P3＝∠P13P14P12＝2x，∴∠P3P2P4＝∠P12P13P11＝3x，…，∠P7P6P8＝∠P8P9P7 ＝7x，∴∠AP7P8＝7x，∠AP8P7＝7x， 在△AP7P8 中，∠A＋∠AP7P8＋∠AP8P7＝180°， 即 x＋7x＋7x＝180°，解得 x＝12°，即∠A＝12°. 答案：12° 3．(2012·山东东营)如图 16－16，在平面直角坐标系 xOy 中，点 A1，A2，A3，… 和点 B1，B2，B3，…分别在直线 y＝kx＋b 和 x 轴上．△OA1B1，△B1A2B2， △B2A3B3，…都是等腰直角三角形．如果 A1(1，1)，A2 7 2 ，3 2 ，那么点 An 的纵 坐标是 ． 图 16－16 点评：(1)本题是一道规律探究题，主要考查等腰直角三角形的性质及图形与坐标 的关系，难度较大． (2)解决本题的关键是先求出 A3，A4 等几个特殊点的纵坐标，然后从中找到一般 规律． 解析：根据图形可知点 A1，A2，A3，A4…的纵坐标为 1，3 2 ，9 4 ，27 8 ，…，综合归 纳得点 An 的纵坐标为 3 2 n－1. 答案： 3 2 n－1 4．(2012·山东枣庄)已知：如图 16－17，在四边形 ABCD 中，∠ABC＝90°，CD⊥AD，AD2＋CD2＝2AB2. (1)求证：AB＝BC； (2)当 BE⊥AD 于点 E 时，求证：BE＝AE＋CD. 点评：(1)本题主要考查勾股定理的应用以及三角形全等的 判定，难度中等． (2)正确添加辅助线是解决本题的关键． 解析：(1)连结 AC，如解图 6. ∵∠ABC＝90°，∴AB2＋BC2＝AC2. ∵CD⊥AD，∴AD2＋CD2＝AC2. ∵AD2＋CD2＝2AB2，∴AB2＋BC2＝2AB2，∴BC2＝AB2. ∵AB＞0，BC＞0，∴AB＝BC. (2)过点 C 作 CF⊥BE 于点 F，如解图 6. ∵BE⊥AD，CF⊥BE，CD⊥AD，∴∠FED＝∠CFE＝∠D＝90°， ∴四边形 CDEF 是矩形．∴CD＝EF. ∵∠ABE＋∠BAE＝90°，∠ABE＋∠CBF＝90°，∴∠BAE＝∠CBF. 在△BAE 与△CBF 中， ∵∠AEB＝∠BFC，∠BAE＝∠CBF，AB＝BC， ∴△BAE≌△CBF(AAS)．∴AE＝BF. ∴BE＝BF＋EF＝AE＋CD. 5．(2012·湖南岳阳) (1)操作发现：如图 16－18①，D 是等边△ABC 的边 BA 上 一动点(点 D 与点 B 不重合)，连结 DC，以 DC 为边在 BC 上方作等边△DCF，连结 AF.你能发现线段 AF 与 BD 之间的数量关系吗？并证明你发现的结论； (2)类比猜想：如图 16－18②，当动点 D 运动至等边△ABC 的边 BA 的延长线上时，其他条件与(1)相同，猜想 AF 与 BD 在(1)中的结论是否仍成立？ 图 16－18 (3)深入探究： Ⅰ.如图 16－18③，当动点 D 在等边△ABC 的边 BA 上运动时(点 D 与点 B 不重合)，连结 DC，以 DC 为边在 BC 上方、下方分别作 等边△DCF 和等边△DCF′，连结 AF，BF′，探究 AF，BF′ 与 AB 有何数量关系？并证明你探究的结论； Ⅱ.如图 16－18④，当动点 D 在等边△ABC 的边 BA 的延长线上运 动时，其他条件与图 16－10③相同，Ⅰ中的结论是否仍成立？ 若不成立，是否有新的结论？并证明你得到的结论． 图 16－18 点评：(1)本题考查全等三角形的判定与性质，等边三角形的性质，是一个 综合型的几何探究题，难度较大． (2)本题充分体现了几何图形中动中有静，变中有定的特点，在探究时可充 分运用类比、猜想、由特殊到一般的归纳法等方法去考虑． 解析：(1)AF＝BD.证明如下：∵△ABC 是等边三角形，∴BC＝AC，∠BCA＝60°. 同理：DC＝CF，∠DCF＝60°.∴∠BCA－∠DCA＝∠DCF－DCA，即∠BCD＝∠ACF. 在△BCD 和△ACF 中，∵BC＝AC，∠BCD＝∠ACF，DC＝FC， ∴△BCD≌△ACF(SAS)，∴BD＝AF. (2)证明过程同(1)，证得△BCD≌△ACF(SAS)，则 AF＝BD(全等三角形的对应边相等)， ∴当动点 D 运动至等边△ABC 的边 BA 的延长线上时，其他条件与(1)相同，∴AF＝BD 仍成立． (3)Ⅰ.AF＋BF′＝AB.证明如下：由(1)知，△BCD≌△ACF(SAS)，则 BD＝AF.同理： △BCF′≌△ACD(SAS)，则 BF′＝AD，∴AF＋BF′＝BD＋AD＝AB. Ⅱ.Ⅰ中的结论不成立．新的结论是 AF＝AB＋BF′.证明：在△BCF′和△ACD 中，∵BC＝ AC，∠BCF′＝∠ACD，F′C＝DC，∴△BCF′≌△ACD(SAS)，∴BF′＝AD. 又由(2)知，AF＝BD，∴AF＝BD＝AB＋AD＝AB＋BF′， 即 AF＝AB＋BF′. 按时完成全程跟踪训练16，全面提升自我！ 单击此处进入全程跟踪训练16