备战2021年九年级中考复习数学考点训练——几何专题：《圆的综合》（四）

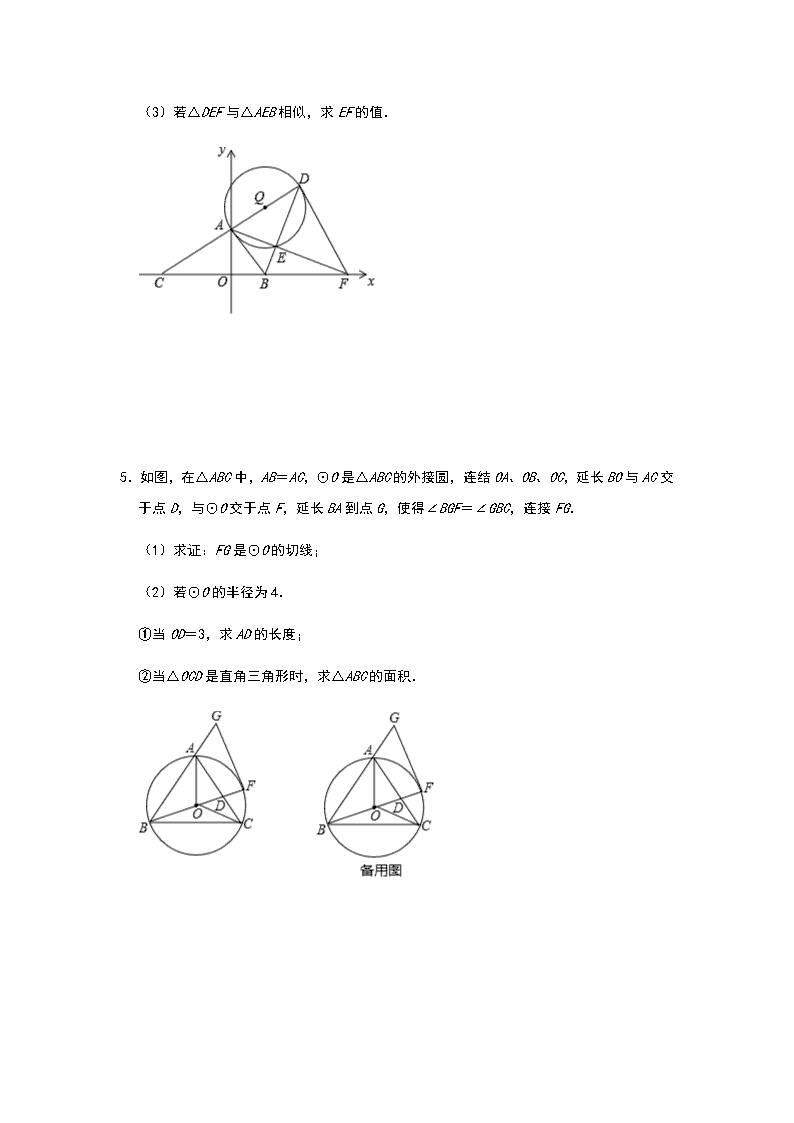
备战2021年九年级中考复习数学考点训练——几何专题：《圆的综合》（四）

备战 2021 年九年级中考数学考点训练——几何专题： 《圆的综合》（四） 1．（1）初步思考： 如图 1，在△PCB 中，已知 PB＝2，BC＝4，N 为 BC 上一点且 BN＝1，试证明：PN＝ PC （2）问题提出： 如图 2，已知正方形 ABCD 的边长为 4，圆 B 的半径为 2，点 P 是圆 B 上的一个动点，求 PD+ PC 的最小值． （3）推广运用： 如图 3，已知菱形 ABCD 的边长为 4，∠B＝60°，圆 B 的半径为 2，点 P 是圆 B 上的一个 动点，求 PD﹣ PC 的最大值． 2．如图，AB 是⊙O 的直径，过点 B 作⊙O 的切线 BM，点 C 为 BM 上一点，连接 AC 与⊙O 交 于点 D，E 为⊙O 上一点，且满足∠EAC＝∠ACB，连接 BD，BE． （1）求证：∠ABE＝2∠CBD； （2）过点 D 作 AB 的垂线，垂足为 F，若 AE＝6，BF＝ ，求⊙O 的半径长． 3．如图，△ABC 中，以 AB 为直径作⊙O，交 BC 于点 D，E 为弧 BD 上一点，连接 AD、DE、AE， 交 BD 于点 F． （1）若∠CAD＝∠AED，求证：AC 为⊙O 的切线； （2）若 DE2＝EF•EA，求证：AE 平分∠BAD； （3）在（2）的条件下，若 AD＝4，DF＝2，求⊙O 的半径． 4．如图，在平面直角坐标系 xOy 中，已知点 A（0，4），点 B 是 x 轴正半轴上一点，连接 AB，过点 A 作 AC⊥AB，交 x 轴于点 C，点 D 是点 C 关于点 A 的对称点，连接 BD，以 AD 为直径作⊙Q 交 BD 于点 E，连接并延长 AE 交 x 轴于点 F，连接 DF． （1）求线段 AE 的长； （2）若 AB﹣BO＝2，求 tan∠AFC 的值； （3）若△DEF 与△AEB 相似，求 EF 的值． 5．如图，在△ABC 中，AB＝AC，⊙O 是△ABC 的外接圆，连结 OA、OB、OC，延长 BO 与 AC 交于点 D，与⊙O 交于点 F，延长 BA 到点 G，使得∠BGF＝∠GBC，连接 FG． （1）求证：FG 是⊙O 的切线； （2）若⊙O 的半径为 4． ①当 OD＝3，求 AD 的长度； ②当△OCD 是直角三角形时，求△ABC 的面积． 6．如图①，在矩形 ABCD 中，AB＝6，BC＝9，点 E 是 BC 边上一动点，连接 AE、DE，作△ECD 的外接⊙O，交 AD 于点 F，交 AE 于点 G，连接 FG． （1）求证△AFG∽△AED； （2）当 BE 的长为 时，△AFG 为等腰三角形； （3）如图②，若 BE＝1，求证：AB 与⊙O 相切． 7．如图 Rt△ABC 中，∠ABC＝90°，P 是斜边 AC 上一个动点，以 BP 为直径作⊙O 交 BC 于 点 D，与 AC 的另一个交点 E，连接 DE． （1）当 时， ①若 ＝130°，求∠C 的度数； ②求证 AB＝AP； （2）当 AB＝15，BC＝20 时 ①是否存在点 P，使得△BDE 是等腰三角形，若存在，求出所有符合条件的 CP 的长； ②以 D 为端点过 P 作射线 DH，作点 O 关于 DE 的对称点 Q 恰好落在∠CPH 内，则 CP 的取 值范围为 ．（直接写出结果） 8．已知：△ABC 是⊙O 的内接三角形，AB 为直径，AC＝BC，D、E 是⊙O 上两点，连接 AD、 DE、AE． （1）如图 1，求证：∠AED﹣∠CAD＝45°； （2）如图 2，若 DE⊥AB 于点 H，过点 D 作 DG⊥AC 于点 G，过点 E 作 EK⊥AD 于点 K，交 AC 于点 F，求证：AF＝2DG； （3）如图 3，在（2）的条件下，连接 DF、CD，若∠CDF＝∠GAD，DK＝3，求⊙O 的半径． 9．如图 1，⊙O 是△ABC 的外接圆，AB 是直径，D 是⊙O 外一点且满足∠DCA＝∠B，连接 AD． （1）求证：CD 是⊙O 的切线； （2）若 AD⊥CD，AB＝10，AD＝8，求 AC 的长； （3）如图 2，当∠DAB＝45°时，AD 与⊙O 交于 E 点，试写出 AC、EC、BC 之间的数量关 系并证明． 10．如图，四边形 ABCD 为菱形，以 AD 为直径作⊙O 交 AB 于点 F，连接 DB 交⊙O 于点 H，E 是 BC 上的一点，且 BE＝BF，连接 DE． （1）求证：△DAF≌△DCE． （2）求证：DE 是⊙O 的切线． （3）若 BF＝2，DH＝ ，求四边形 ABCD 的面积． 参考答案 1．（1）证明：如图 1， ∵PB＝2，BC＝4，BN＝1， ∴PB2＝4，BN•BC＝4． ∴PB2＝BN•BC． ∴ ＝ ． 又∵∠B＝∠B， ∴△BPN∽△BCP． ∴ ＝ ＝ ． ∴PN＝ PC； （2）如图 2，在 BC 上取一点 G，使得 BG＝1， （3）同（2）中证法，如图 3， 取 BG＝1， 当点 P 在 DG 的延长线上时，PD﹣ PC 的最大值，最大值为 ． 2．解：（1）∵AB 是⊙O 的直径， ∴∠ADB＝90°，即∠DAB+∠DBA＝90°， ∵BM 是⊙O 的切线， ∴AB⊥BC， ∴∠ABC＝90°，即∠CBD+∠DBA＝90°， ∴∠DAB＝∠CBD， ∵∠ABC＝90°， ∴∠ACB＝90°﹣∠BAC， ∵∠EAC＝∠ACB， ∴∠EAC＝90°﹣∠BAC ＝90°﹣（∠EAC﹣∠BAE）， ∴∠BAE＝2∠EAC﹣90°， ∵AB 是直径， ∴∠AEB＝90°， ∴∠ABE＝90°﹣∠BAE ＝90°﹣（2∠EAC﹣90°） ＝2（90°﹣∠EAC） ＝2（90°﹣∠ACB） ＝2∠CAB ＝2∠CBD． ∴∠ABE＝2∠CBD； （2）如图，连接 DO 并延长交 AE 于点 G， ∵∠DOB＝2∠BAD， ∠ABE＝2∠CAB， ∴∠DOB＝∠ABE， ∴DG∥BE， ∴∠AGO＝∠AEB＝90°， ∴AG＝EG＝ AE＝3， ∠AOG＝∠DOF， OA＝OD， ∴△AOG≌△DOF（AAS） ∴DF＝AG＝3， 又 OF＝OB﹣BF＝OD﹣ ， 在 Rt△DOF 中，根据勾股定理，得 OD2＝DF2+OF2， 即 OD2＝32+（OD﹣ ）2， 解得 OD＝ ． 答：⊙O 的半径长为 ． 3．证明：（1）∵AB 是直径， ∴∠BDA＝90°， ∴∠DBA+∠DAB＝90°， ∵∠CAD＝∠AED，∠AED＝∠ABD， ∴∠CAD＝∠ABD， ∴∠CAD+∠DAB＝90°， ∴∠BAC＝90°， 即 AB⊥AC，且 AO 是半径， ∴AC 为⊙O 的切线； （2）∵DE2＝EF•EA， ∴ ，且∠DEF＝∠DEA， ∴△DEF∽△AED， ∴∠EDF＝∠DAE， ∵∠EDF＝∠BAE， ∴∠BAE＝∠DAE， ∴AE 平分∠BAD； （3）如图，过点 F 作 FH⊥AB，垂足为 H， ∵AE 平分∠BAD，FH⊥AB，∠BDA＝90°， ∴DF＝FH＝2， ∵S△ABF＝ AB×FH＝ ×BF×AD， ∴2AB＝4BF， ∴AB＝2BF， 在 Rt△ABD 中，AB2＝BD2+AD2， ∴（2BF）2＝（2+BF）2+16， ∴BF＝ ，BF＝﹣2（不合题意舍去） ∴AB＝ ， ∴⊙O 的半径为 ． 4．解：（1）∵点 A（0，4）， ∴AO＝4， ∵AD 是⊙Q 的直径， ∴∠AEB＝∠AED＝90°， ∴∠AEB＝∠AOB＝90°， ∵BA 垂直平分 CD， ∴BC＝BD ∴∠ABO＝∠ABE 在△ABE 和△ABO 中， ， ∴△ABE≌△ABO（AAS） ∴AE＝AO＝4； （2）设 BO＝x，则 AB＝x+2， 在 Rt△ABO 中，由 AO2+OB2＝AB2 得：42+x2＝（x+2）2， 解得：x＝3， ∴OB＝BE＝3，AB＝5， ∵∠EAB+∠ABE＝90°，∠ACB+∠ABC＝90°， ∴∠EAB＝∠ACB， ∵∠BFA＝∠AFC， ∴△BFA∽△AFC ∴ ＝ ＝ ， 设 EF＝x，则 AF＝4+x，BF＝ （4+x）， ∵在 Rt△BEF 中，BE2+EF2＝BF2， ∴32+x2＝[ （4+x）]2， 解得：x＝ ，即 EF＝ ， ∴tan∠AFC＝ ＝ ＝ ； （3）①当△DEF∽△AEB 时，∠BAE＝∠FDE， ∴∠ADE＝∠FDE， ∴BD 垂直平分 AF， ∴EF＝AE＝4； ②当△DEF∽△BEA 时，∠ABE＝∠FDE， ∴AB∥DF， ∴∠ADF＝∠CAB＝90°， ∴DF 相切⊙Q， ∴∠DAE＝∠FDE， 设⊙Q 交 y 轴于点 G，连接 DG，作 FH⊥DG 于 H，如图所示： 则∠FDH＝∠DAG，四边形 OGHF 是矩形， ∴OG＝FH， ∵△ABE≌△ABO， ∴∠OAB＝∠EAB， ∵AB⊥AD， ∴∠DAE＝∠CAO， ∵∠CAO＝∠DAE， ∴∠DAE＝∠DAE， ∴∠DAE＝∠DAG＝∠FDE＝∠FDH， ∴AG＝AE＝4， ∴EF＝FH＝OG＝AO+AG＝4+4＝8， 综上所述，若△DEF 与△AEB 相似，EF 的值为 4 或 8． 5．（1）证明：连接 AF， ∵BF 为⊙O 的直径， ∴∠BAF＝90°，∠FAG＝90°， ∴∠BGF+∠AFG＝90°， ∵AB＝AC， ∴∠ABC＝∠ACB， ∵∠ACB＝∠AFB，∠BGF＝∠ABC， ∴∠BGF＝∠AFB， ∴∠AFB+∠AFG＝90°，即∠OFG＝90°， 又∵OF 为半径， ∴FG 是⊙O 的切线； （2）解：①连接 CF，则∠ACF＝∠ABF， ∵AB＝AC，AO＝AO，BO＝CO， ∴△ABO≌△ACO（SSS）， ∴∠ABO＝∠BAO＝∠CAO＝∠ACO， ∴∠CAO＝∠ACF， ∴AO∥CF， ∴ ＝ ， ∵半径是 4，OD＝3， ∴DF＝1，BD＝7， ∴ ＝ ＝3，即 CD＝ AD， ∵∠ABD＝∠FCD，∠ADB＝∠FDC， ∴△ADB∽△FDC， ∴ ＝ ， ∴AD•CD＝BD•DF， ∴AD•CD＝7，即 AD2＝7， ∴AD＝ （取正值）； ②∵△ODC 为直角三角形，∠DCO 不可能等于 90°， ∴存在∠ODC＝90°或∠COD＝90°， 当∠ODC＝90°时， ∵∠ACO＝∠ACF， ∴OD＝DF＝2，BD＝6， ∴AD＝CD， ∴AD•CD＝AD2＝12， ∴AD＝2 ，AC＝4 ， ∴S△ABC＝ ×4 ×6＝12 ； 当∠COD＝90°时， ∵OB＝OC＝4， ∴△OBC 是等腰直角三角形， ∴BC＝4 ， 延长 AO 交 BC 于点 M， 则 AM⊥BC， ∴MO＝2 ， ∴AM＝4+2 ， ∴S△ABC＝ ×4 ×（4+2 ）＝8 +8， ∴△ABC 的面积为 12 或 8 +8． 6．（1）证明：∵四边形 FGED 是⊙O 的内接四边形， ∴∠FGE+∠ADE＝180°， ∵∠AGF+∠FGE＝180°， ∴∠AGF＝∠ADE， 又∠GAF＝∠DAE， ∴△AFG∽△AED； （2）解：由（1）得：△AFG∽△AED， ∴当△AED 为等腰三角形时，△AFG 为等腰三角形， 连接 EF，如图①所示： ∵四边形 ABCD 是矩形，AB＝6，BC ＝9， ∴CD＝AB＝6，AD＝BC＝9，∠BAD＝∠ABC＝∠BCD＝∠ADC＝90°， ∵⊙O 是△ECD 的外接圆，∠ECD＝90°， ∴DE 是⊙O 的直径， ∴∠DFE＝90°， ∴∠AFE＝180°﹣∠DFE＝180°﹣90°＝90°， ∴∠BAF＝∠ABE＝∠AFE＝90°， ∴四边形 ABEF 是矩形， ∴AF＝BE，EF＝AB＝6， △AED 为等腰三角形，分三种情况： ①当 AE＝DE 时， ∵∠DFE＝90°， ∴AF＝DF＝ AD＝ ×9＝ ， ∴BE＝AF＝ ； ②当 DE＝AD＝9 时， 在 Rt△DCE 中，由勾股定理得：CE＝ ＝ ＝3 ， ∴BE＝BC﹣CE＝9﹣3 ； ③当 AE＝AD＝9 时， 在 Rt△ABE 中，由勾股定理得：BE＝ ＝ ＝3 ； 综上所述，当 BE 的长为 或 9﹣3 或 3 时，△AFG 为等腰三角形， 故答案为： 或 9﹣3 或 3 ； （3）证明：过 O 作 OH⊥AB 于点 H，反向延长 OH 交 CD 于点 I，如图②所示： 则∠AHI＝90°， ∵四边形 ABCD 是矩形， ∴CD＝AB＝6，∠BCD＝∠BAD＝∠ADC＝90°， ∴∠AHI＝∠BAD＝∠ADC＝90°， ∴四边形 AHID 为矩形， ∴HI＝AD＝9，∠OID＝90°， ∴∠ECD＝∠OID， ∴OI∥CE， ∵∠BCD＝90°， ∴DE 为直径， ∴OD＝OE， ∴OI 是△DCE 的中位线， ∴DI＝ CD＝3，OI＝ EC， ∵BE＝1，BC＝9， ∴EC＝8， ∴OI＝ ×8＝4， ∴OH＝HI﹣OI＝9﹣4＝5， 在 Rt△DEC 中，由勾股定理得：DE＝ ＝ ＝10， ∴⊙O 的半径 OD＝5 ∴OH 是⊙O 的半径， 又 OH⊥AB， ∴AB 与⊙O 相切． 7．（1）①解：连接 BE，如图 1 所示： ∵BP 是直径， ∴∠BEC＝90°， ∵ ＝130°， ∴ ＝50°， ∵ ＝ ， ∴ ＝100°， ∴∠CBE＝50°， ∴∠C＝40°； ②证明：∵ ＝ ， ∴∠CBP＝∠EBP， ∵∠ABE+∠A＝90°，∠C+∠A＝90°， ∴∠C＝∠ABE，∵∠APB＝∠CBP+∠C，∠ABP＝∠EBP+∠ABE， ∴∠APB＝∠ABP， ∴AP＝AB； （2）解：①由 AB＝15，BC＝20， 由勾股定理得：AC＝ ＝ ＝25， ∵ AB•BC＝ AC•BE， 即 ×15×20＝ ×25×BE ∴BE＝12， 连接 DP，如图 1﹣1 所示： ∵BP 是直径， ∴∠PDB＝90°， ∵∠ABC＝90°， ∴PD∥AB， ∴△DCP∽△BCA， ∴ ＝ ， ∴CP＝ ＝ ＝ CD， △BDE 是等腰三角形，分三种情况： 当 BD＝BE 时，BD＝BE＝12， ∴CD＝BC﹣BD＝20﹣12＝8， ∴CP＝ CD＝ ×8＝10； 当 BD＝ED 时，可知点 D 是 Rt△CBE 斜边的中线， ∴CD＝ BC＝10， ∴CP＝ CD＝ ×10＝ ； 当 DE＝BE 时，作 EH⊥BC，则 H 是 BD 中点，EH∥AB，如图 1﹣2 所示： AE＝ ＝ ＝9， ∴CE＝AC﹣AE＝25﹣9＝16，CH＝BC﹣BH＝20﹣BH， ∵EH∥AB， ∴ ＝ ， 即 ＝ ， 解得：BH＝ ， ∴BD＝2BH＝ ， ∴CD＝BC﹣BD＝20﹣ ＝ ， ∴CP＝ CD＝ × ＝7； 综上所述，△BDE 是等腰三角形，符合条件的 CP 的长为 10 或 或 7； ②当点 Q 落在∠CPH 的边 PH 上时，CP 最小，如图 2 所示： 连接 OD、OQ、OE、QE、BE， 由对称的性质得：DE 垂直平分 OQ， ∴OD＝QD，OE＝QE， ∵OD＝OE， ∴OD＝OE＝QD＝QE， ∴四边形 ODQE 是菱形， ∴PQ∥OE， ∵PB 为直径， ∴∠PDB＝90°， ∴PD⊥BC， ∵∠ABC＝90°， ∴AB⊥BC， ∴PD∥AB， ∴DE∥AB， ∵OB＝OP， ∴OE 为△ABP 中位线， ∴PE＝AE＝9， ∴PC＝AC﹣PE﹣AE＝25﹣9﹣9＝7； 当点 Q 落在∠CPH 的边 PC 上时，CP 最大，如图 3 所示： 连接 OD、OQ、OE、QD， 同理得：四边形 ODQE 是菱形， ∴OD∥QE， 连接 DF， ∵∠DBA＝90°， ∴DF 是直径， ∴D、O、F 三点共线， ∴DF∥AQ， ∴∠OFB＝∠A， ∵OB＝OF， ∴∠OFB＝∠OBF＝∠A， ∴PA＝PB， ∵∠OBF+∠CBP＝∠A+∠C＝90°， ∴∠CBP＝∠C， ∴PB＝PC＝PA， ∴PC＝ AC＝12.5， ∴7＜CP＜12.5， 故答案为：7＜CP＜12.5． 8．（1）证明：如图 1，连接 CO，CE， ∵AB 是直径， ∴∠ACB＝90°， ∵AC＝BC， ∴∠B＝∠CAB＝45°， ∴∠COA＝2∠B＝90°， ∵ ， ∴∠CAD＝∠CED， ∴∠AED﹣∠CAD＝∠AED﹣∠CED＝∠AEC＝ ∠COA＝45°， 即∠AED﹣∠CAD＝45°； （2）如图 2，连接 CO 并延长，交⊙O 于点 N，连接 AN，过点 E 作 EM⊥AC 于 M， 则∠CAN＝90°， ∵AC＝BC，AO＝BO， ∴CN⊥AB， ∴AB 垂直平分 CN， ∴AN＝AC， ∴∠NAB＝∠CAB， ∵AB 垂直平分 DE， ∴AD＝AE， ∴∠DAB＝∠EAB， ∴∠NAB﹣∠EAB＝∠CAB﹣∠DAB， 即∠GAD＝∠NAE， ∵∠CAN＝∠CME＝90°， ∴AN∥EM， ∴∠NAE＝∠MEA， ∴∠GAD＝∠MEA， 又∵∠G＝∠AME＝90°，AD＝EA， ∴△ADG≌△EAM（AAS）， ∴AG＝EM，AM＝DG， 又∵∠MEF+∠MFE＝90°，∠MFE+∠GAD＝90°， ∴∠MEF＝∠GAD， 又∵∠G＝∠FME＝90°， ∴△ADG≌△EFM（ASA）， ∴DG＝MF， ∵DG＝AM， ∴AF＝AM+MF＝2DG； （3）∵∠CDF＝∠GAD，∠FCD＝∠DCA， ∴△FCD∽△DCA， ∴∠CFD＝∠CDA＝∠CBA， ∵AC＝BC，AB 为直径， ∴△ABC 为等腰直角三角形， ∴∠CFD＝∠CDA＝∠CBA＝45°， ∴△GFD 为等腰直角三角形， 设 GF＝GD＝a，则 FD＝ a，AF＝2a， ∴ ＝ ＝ ， ∵∠FAK＝∠DAG，∠AKF＝∠G＝90°， ∴△AFK∽△ADG， ∴ ＝ ＝ ， 在 Rt△AFK 中， 设 FK＝x，则 AK＝3x， ∵FK2+AK2＝AF2， ∴x2+（3x）2＝（2a）2， 解得，x＝ a（取正值）， ∴FK＝ a， 在 Rt△FKD 中，FK2+DK2＝FD2， ∴（ a）2+32＝（ a）2， 解得，a＝ （取正值）， ∴GF＝GD＝ ，AF＝ ， ∵△FCD∽△DCA， ∴ ＝ ， ∴CD2＝CA•FC， ∵CD2＝CG2+GD2， ∴CG2+GD2＝CA•FC， 设 FC＝n， 则（ ﹣n）2+（ ）2＝（ +n）n， 解得，n＝ ， ∴AC＝AF+CF＝ + ＝ ， ∴AB＝ AC＝ ， ⊙O 的半径为 ． 9．（1）证明：连接 OC，如图 1 所示： ∵AB 是⊙O 的直径， ∴∠ACB＝90°， ∵OC＝OB， ∴∠B＝∠OCB， ∵∠DCA＝∠B， ∴∠DCA＝∠OCB， ∴∠DCO＝∠DCA+∠OCA＝∠OCB+∠OCA＝∠ACB＝90°， ∴CD⊥OC， ∴CD 是⊙O 的切线； （2）解：∵AD⊥CD ∴∠ADC＝∠ACB＝90° 又∵∠DCA＝∠B ∴△ACD∽△ABC ∴ ＝ ，即 ＝ ， ∴AC＝4 ， 即 AC 的长为 4 ； （3）解：AC＝BC+ EC；理由如下： 在 AC 上截取 AF 使 AF＝BC，连接 EF、BE，如图 2 所示： ∵AB 是直径， ∴∠ACB＝∠AEB＝90°， ∵∠DAB＝45°， ∴△AEB 为等腰直角三角形， ∴∠EAB＝∠EBA＝∠ECA＝45°，AE＝BE， 在△AEF 和△BEC 中， ， ∴△AEF≌△BEC（SAS）， ∴EF＝CE，∠AFE＝∠BCE＝∠ACB+∠ECA＝90°+45°＝135°， ∴∠EFC＝180°﹣∠AFE＝180°﹣135°＝45°， ∴∠EFC＝∠ECF＝45°， ∴△EFC 为等腰直角三角形． ∴CF＝ EC， ∴AC＝AF+CF＝BC+ EC． 10．（1）证明：如图，连接 DF， ∵四边形 ABCD 为菱形， ∴AB＝BC＝CD＝DA，AD∥BC，∠DAB＝∠C， ∵BF＝BE， ∴AB﹣BF＝BC﹣BE， 即 AF＝CE， ∴△DAF≌△DCE（SAS）； （2）由（1）知，△DAF≌△DCE，则∠DFA＝∠DEC． ∵AD 是⊙O 的直径， ∴∠DFA＝90°，∴∠DEC＝90° ∵AD∥BC， ∴∠ADE＝∠DEC＝90°， ∴OD⊥DE， ∵OD 是⊙O 的半径， ∴DE 是⊙O 的切线； （2）解：如图，连接 AH， ∵AD 是⊙O 的直径， ∴∠AHD＝∠DFA＝90°， ∴∠DFB＝90°， ∵AD＝AB，DH＝ ， ∴DB＝2DH＝2 ， 在 Rt△ADF 和 Rt△BDF 中， ∵DF2＝AD2﹣AF2，DF2＝BD2﹣BF2， ∴AD2﹣AF2＝DB2﹣BF2， ∴AD2﹣（AD﹣BF）2＝DB2﹣BF2， ∴AD2﹣（AD﹣2）2＝（2 ）2﹣22， ∴AD＝5． ∴AH＝ ＝ ＝2 ∴S 四边形 ABCD＝2S△ABD＝2× •AH＝BD•AH＝2 ×2 ＝20．即四边形 ABCD 的面积是 20．