高考数学专题复习教案： 三角函数的图象与性质

高考数学专题复习教案： 三角函数的图象与性质

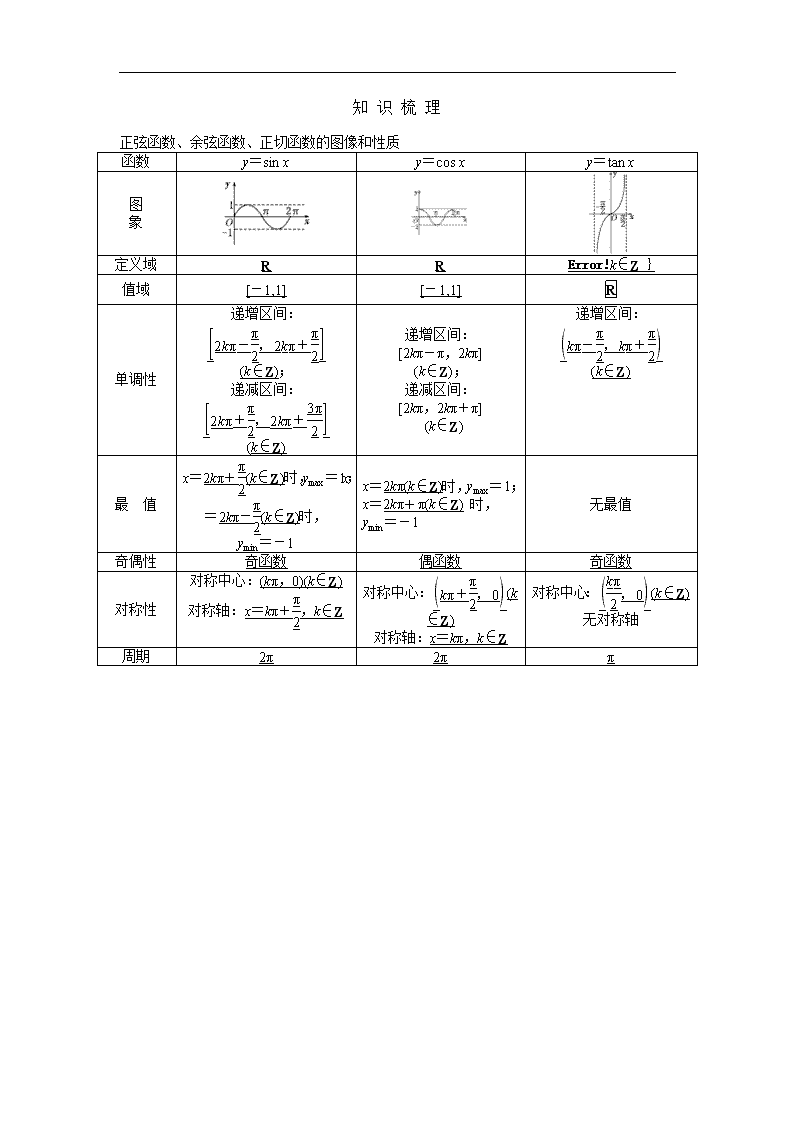
三角函数的图象与性质 主标题：三角函数的图象与性质 副标题：为学生详细的分析三角函数的图象与性质的高考考点、命题方向以及规律总结。‎ 关键词：三角函数，正弦函数，余弦函数，图象与性质 难度：2‎ 重要程度：4‎ 考点剖析：‎ ‎1．能画出y＝sin x，y＝cos x，y＝tan x的图象，了解三角函数的周期性．‎ ‎2．借助图象理解正弦函数、余弦函数在[0,2π]，正切函数在上的性质.‎ 命题方向：‎ ‎1．三角函数的单调性是每年高考命题的热点，题型既有选择题也有填空题，难度适中，为中低档题．‎ ‎2．高考对三角函数单调性的考查有以下几个命题角度：‎ ‎(1)求已知三角函数的单调区间；‎ ‎(2)已知三角函数的单调区间求参数；‎ ‎(3)利用三角函数的单调性求值域(或最值)．‎ 规律总结：‎ 2个性质——周期性与奇偶性 ‎　(1)周期性 函数y＝Asin(ωx＋φ)和y＝Acos(ωx＋φ)的最小正周期为，y＝tan(ωx＋φ)的最小正周期为.‎ ‎(2)奇偶性 三角函数中奇函数一般可化为y＝Asin ωx或y＝Atan ωx的形式，而偶函数一般可化为y＝Acos ωx＋b的形式．‎ 3种方法——求三角函数值域(或最值)的方法 ‎　(1)利用sin x、cos x的有界性．‎ ‎(2)形式复杂的函数应化为y＝Asin(ωx＋φ)＋k的形式，逐步分析ωx＋φ的范围，根据正弦函数单调性写出函数的值域(或最值)．‎ ‎(3)换元法：把sin x或cos x看作一个整体，可化为求函数在区间上的值域(或最值)问题．‎ 4个注意点——研究三角函数性质应注意的问题 ‎　(1)三角函数的图像从形上完全反映了三角函数的性质，求三角函数的定义域、值域时应注意利用三角函数的图像．‎ ‎(2)闭区间上值域(或最值)问题，首先要在定义域基础上分析单调性，含参数的值域(或最值)问题，要讨论参数对值域(或最值)的影响．‎ ‎(3)利用换元法求复合函数的单调性时，要注意x系数的正负．‎ ‎(4)利用换元法求三角函数值域(或最值)时要注意三角函数的有界性，如：y＝sin2x－4sin x＋5，令t＝sin x，则y＝(t－2)2＋1≥1，解法错误．‎ 知 识 梳 理 正弦函数、余弦函数、正切函数的图像和性质 函数 y＝sin x y＝cos x y＝tan x 图 象 定义域 R R k∈Z }‎ 值域 ‎[－1,1]‎ ‎[－1,1]‎ R 单调性 递增区间：‎ ‎(k∈Z)；‎ 递减区间：‎ ‎(k∈Z)‎ 递增区间：‎ ‎[2kπ－π，2kπ] ‎ ‎(k∈Z)；‎ 递减区间：‎ ‎[2kπ，2kπ＋π]‎ ‎ (k∈Z)‎ 递增区间： ‎(k∈Z)‎ 最　值 x＝2kπ＋(k∈Z)时，ymax＝1；x＝2kπ－(k∈Z)时，‎ ymin＝－1‎ x＝2kπ(k∈Z)时，ymax＝1；‎ x＝2kπ＋π(k∈Z) 时，‎ ymin＝－1‎ 无最值 奇偶性 奇函数 偶函数 奇函数 对称性 对称中心：(kπ，0)(k∈Z)‎ 对称轴：x＝kπ＋，k∈Z 对称中心：(k∈Z)‎ 对称轴：x＝kπ，k∈Z 对称中心：(k∈Z)‎ 无对称轴 周期 ‎2π ‎2π π