(超强精品)高考数学第一轮系统复习资料 (2)
第一章 集合
第一节 集合的含义、表示及基本关系
A组
1.已知A={1,2},B={x|x∈A},则集合A与B的关系为________.
2.若∅{x|x2≤a,a∈R},则实数a的取值范围是________.
3.已知集合A={y|y=x2-2x-1,x∈R},集合B={x|-2≤x<8},则集合A与B的关系是________.
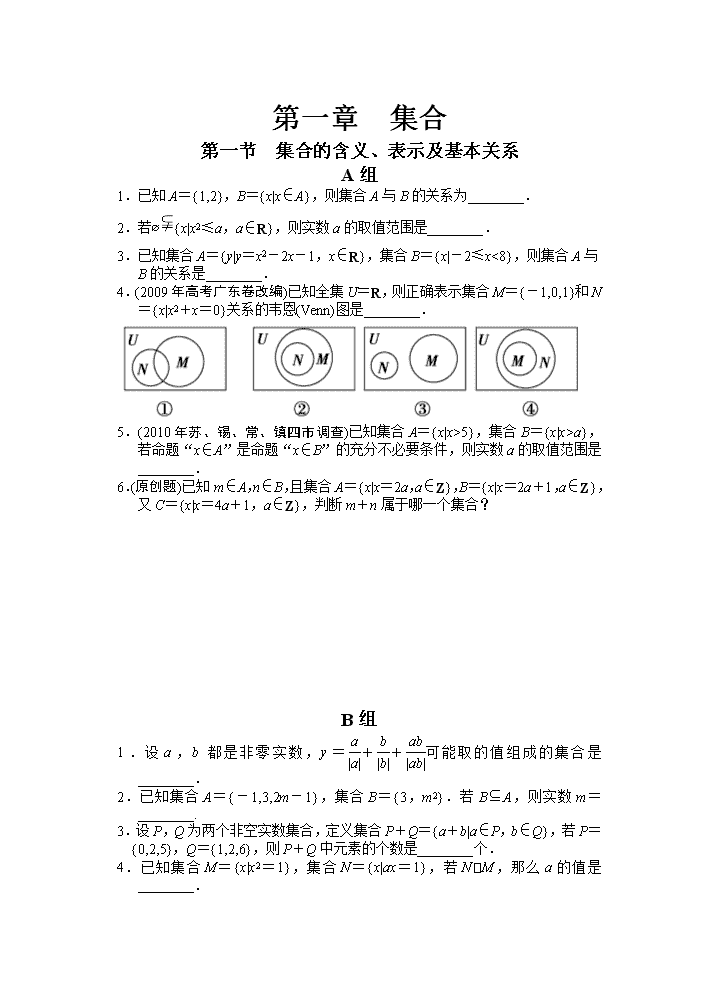
4.(2009年高考广东卷改编)已知全集U=R,则正确表示集合M={-1,0,1}和N={x|x2+x=0}关系的韦恩(Venn)图是________.
5.(2010年苏、锡、常、镇四市调查)已知集合A={x|x>5},集合B={x|x>a},若命题“x∈A”是命题“x∈B”的充分不必要条件,则实数a的取值范围是________.
6.(原创题)已知m∈A,n∈B,且集合A={x|x=2a,a∈Z},B={x|x=2a+1,a∈Z},又C={x|x=4a+1,a∈Z},判断m+n属于哪一个集合?
B组
1.设a,b都是非零实数,y=++可能取的值组成的集合是________.
2.已知集合A={-1,3,2m-1},集合B={3,m2}.若B⊆A,则实数m=________.
3.设P,Q为两个非空实数集合,定义集合P+Q={a+b|a∈P,b∈Q},若P={0,2,5},Q={1,2,6},则P+Q中元素的个数是________个.
4.已知集合M={x|x2=1},集合N={x|ax=1},若NM,那么a的值是________.
5.满足{1}A⊆{1,2,3}的集合A的个数是________个.
6.已知集合A={x|x=a+,a∈Z},B={x|x=-,b∈Z},C={x|x=+,c∈Z},则A、B、C之间的关系是________.
7.集合A={x||x|≤4,x∈R},B={x|x
5”的________条件.
8.(2010年江苏启东模拟)设集合M={m|m=2n,n∈N,且m<500},则M中所有元素的和为________.
9.(2009年高考北京卷)设A是整数集的一个非空子集,对于k∈A,如果k-1∉A,且k+1∉A,那么称k是A的一个“孤立元”.给定S={1,2,3,4,5,6,7,8},由S的3个元素构成的所有集合中,不含“孤立元”的集合共有________个.
10.已知A={x,xy,lg(xy)},B={0,|x|,y},且A=B,试求x,y的值.
11.已知集合A={x|x2-3x-10≤0},
(1)若B⊆A,B={x|m+1≤x≤2m-1},求实数m的取值范围;
(2)若A⊆B,B={x|m-6≤x≤2m-1},求实数m的取值范围;
(3)若A=B,B={x|m-6≤x≤2m-1},求实数m的取值范围.
12.已知集合A={x|x2-3x+2≤0},B={x|x2-(a+1)x+a≤0}.
(1)若A是B的真子集,求a的取值范围;
(2)若B是A的子集,求a的取值范围;
(3)若A=B,求a的取值范围.
第二节 集合的基本运算
A组
1.(2009年高考浙江卷改编)设U=R,A={x|x>0},B={x|x>1},则A∩∁UB=________.
2.(2009年高考全国卷Ⅰ改编)设集合A={4,5,7,9},B={3,4,7,8,9},全集U=A∪B,则集合∁U(A∩B)中的元素共有________个.
3.已知集合M={0,1,2},N={x|x=2a,a∈M},则集合M∩N=________.
4.(原创题)设A,B是非空集合,定义AⓐB={x|x∈A∪B且x∉A∩B},已知A={x|0≤x≤2},B={y|y≥0},则AⓐB=________.
5.(2009年高考湖南卷)某班共30人,其中15人喜爱篮球运动,10人喜爱乒乓球运动,8人对这两项运动都不喜爱,则喜爱篮球运动但不喜爱乒乓球运动的人数为________.
6.(2010年浙江嘉兴质检)已知集合A={x|x>1},集合B={x|m≤x≤m+3}.
(1)当m=-1时,求A∩B,A∪B;
(2)若B⊆A,求m的取值范围.
B组
1.若集合M={x∈R|-31的这样的函数个数有________个.
5.(原创题)由等式x3+a1x2+a2x+a3=(x+1)3+b1(x+1)2+b2(x+1)+b3定义一个映射f(a1,a2,a3)=(b1,b2,b3),则f(2,1,-1)=________.
6.已知函数f(x)=
(1)求f(1-),f{f[f(-2)]}的值;(2)求f(3x-1);(3)若f(a)=, 求a.
B组
1.(2010年广东江门质检)函数y=+lg(2x-1)的定义域是________.
2.(2010年山东枣庄模拟)函数f(x)=则f(f(f()+5))=________.
3.定义在区间(-1,1)上的函数f(x)满足2f(x)-f(-x)=lg(x+1),则f(x)的解析式为________.
4.设函数y=f(x)满足f(x+1)=f(x)+1,则函数y=f(x)与y=x图象交点的个数可能是_____个。
5.设函数f(x)=,若f(-4)=f(0),f(-2)=-2,则f(x)的解析式为f(x)=________,关于x的方程f(x)=x的解的个数为________个.
6.设函数f(x)=logax(a>0,a≠1),函数g(x)=-x2+bx+c,若f(2+)-f(+1)=,g(x)的图象过点A(4,-5)及B(-2,-5),则a=__________,函数f[g(x)]的定义域为__________.
7.(2009年高考天津卷改编)设函数f(x)=,则不等式f(x)>f(1)的解集是________.
8.(2009年高考山东卷)定义在R上的函数f(x)满足f(x)=则f(3)的值为________.
9.有一个有进水管和出水管的容器,每单位时间进水量是一定的,设从某时刻开始,5分钟内只进水,不出水,在随后的15分钟内既进水,又出水,得到时间x与容器中的水量y之间关系如图.再随后,只放水不进水,水放完为止,则这段时间内(即x≥20),y与x之间函数的函数关系是________.
10.函数f(x)=.
(1)若f(x)的定义域为R,求实数a的取值范围;
(2)若f(x)的定义域为[-2,1],求实数a的值.
11.已知f(x+2)=f(x)(x∈R),并且当x∈[-1,1]时,f(x)=-x2+1,求当x∈[2k-1,2k+1](k∈Z)时、f(x)的解析式.
12.在2008年11月4日珠海航展上,中国自主研制的ARJ 21支线客机备受关注,接到了包括美国在内的多国订单.某工厂有216名工人接受了生产1000件该支线客机某零部件的总任务,已知每件零件由4个C型装置和3个H型装置配套组成,每个工人每小时能加工6个C型装置或3个H型装置.现将工人分成两组同时开始加工,每组分别加工一种装置,设加工C型装置的工人有x位,他们加工完C型装置所需时间为g(x),其余工人加工完H型装置所需时间为h(x).(单位:h,时间可不为整数)
(1)写出g(x),h(x)的解析式;
(2)写出这216名工人完成总任务的时间f(x)的解析式;
(3)应怎样分组,才能使完成总任务的时间最少?
第二节 函数的单调性
A组
1.(2009年高考福建卷改编)下列函数f(x)中,满足“对任意x1,x2∈(0,+∞),当x1f(x2)”的是________.
①f(x)= ②f(x)=(x-1)2
③f(x)=ex ④f(x)=ln(x+1)
2.函数f(x)(x∈R)的图象如右图所示,则函数g(x)= f(logax)(00)在(,+∞)上是单调增函数,则实数a的取值范围是________.
4.(2009年高考陕西卷改编)定义在R上的偶函数f(x),对任意x1,x2∈[0,+
∞)(x1≠x2),有<0,则下列结论正确的是________.
①f(3)0,a≠1)在区间(0,)内恒有f(x)>0,则f(x)的单调递增区间为__________.
10.试讨论函数y=2(logx)2-2logx+1的单调性.
11.(2010年广西河池模拟)已知定义在区间(0,+∞)上的函数f(x)满足f()=f(x1)-f(x2),且当x>1时,f(x)<0.
(1)求f(1)的值;(2)判断f(x)的单调性;(3)若f(3)=-1,解不等式f(|x|)<-2.
12.已知:f(x)=log3,x∈(0,+∞),是否存在实数a,b,使f(x)同时满足下列三个条件:(1)在(0,1]上是减函数,(2)在[1,+∞)上是增函数,(3)f(x)的最小值是1.若存在,求出a、b;若不存在,说明理由.
第三节 函数的性质
A组
1.设偶函数f(x)=loga|x-b|在(-∞,0)上单调递增,则f(a+1)与f(b+2)的大小关系为________.
2.(2010年广东三校模拟)定义在R上的函数f(x)既是奇函数又是以2为周期的周期函数,则f(1)+f(4)+f(7)等于________.
3.(2009年高考山东卷改编)已知定义在R上的奇函数f(x)满足f(x-4)=-f(x),且在区间[0,2]上是增函数,则f(-25)、f(11)、f(80)的大小关系为________.
4.(2009年高考辽宁卷改编)已知偶函数f(x)在区间[0,+∞)上单调增加,则满足f(2x-1)0,若f(-1)=0,那么关于x的不等式xf(x)<0的解集是________.
5.(2009年高考江西卷改编)已知函数f(x)是(-∞,+∞)上的偶函数,若对于x≥0,都有f(x+2)=f(x),且当x∈[0,2)时,f(x)=log2(x+1),则f(-2009)+f(2010)的值为________.
6.(2010年江苏苏州模拟)已知函数f(x)是偶函数,并且对于定义域内任意的x,满足f(x+2)=-,若当2a,且|x1-a|<|x2-a|时,则f(2a-x1)与f(x2)的大小关系为________.
8.已知函数f(x)为R上的奇函数,当x≥0时,f(x)=x(x+1).若f(a)=-2,则实数a=________.
9.(2009年高考山东卷)已知定义在R上的奇函数f(x)满足f(x-4)=-f(x),且在区间[0,2]上是增函数.若方程f(x)=m(m>0)在区间[-8,8]上有四个不同的根x1,x2,x3,x4,则x1+x2+x3+x4=________.
10.已知f(x)是R上的奇函数,且当x∈(-∞,0)时,f(x)=-xlg(2-x),求f(x)的解析式.
11.已知函数f(x),当x,y∈R时,恒有f(x+y)=f(x)+f(y).
(1)求证:f(x)是奇函数;
(2)如果x∈R+,f(x)<0,并且f(1)=-,试求f(x)在区间[-2,6]上的最值.
12.已知函数f(x)的定义域为R,且满足f(x+2)=-f(x).
(1)求证:f(x)是周期函数;
(2)若f(x)为奇函数,且当0≤x≤1时,f(x)=x,求使f(x)=-在[0,2010]上的所有x的个数.
第三章 指数函数和对数函数
第一节 指数函数
A组
1.(2010年黑龙江哈尔滨模拟)若a>1,b<0,且ab+a-b=2,则ab-a-b的值等于________.
2.已知f(x)=ax+b的图象如图所示,则f(3)=________.
3.函数y=()2x-x2的值域是________.
4.(2009年高考山东卷)若函数f(x)=ax-x-a(a>0,且a≠1)有两个零点,则实数a的取值范围是________.
5.(原创题)若函数f(x)=ax-1(a>0,a≠1)的定义域和值域都是[0,2],则实数a等于________.
6.已知定义域为R的函数f(x)=是奇函数.
(1)求a,b的值;
(2)若对任意的t∈R,不等式f(t2-2t)+f(2t2-k)<0恒成立,求k的取值范围.
B组
1.如果函数f(x)=ax+b-1(a>0且a≠1)的图象经过第一、二、四象限,不经过第三象限,那么一定有________.
①00 ②01且b<0 ④a>1且b>0
2.(2010年保定模拟)若f(x)=-x2+2ax与g(x)=(a+1)1-x在区间[1,2]上都是减函数,则a的取值范围是________.
3.已知f(x),g(x)都是定义在R上的函数,且满足以下条件:
①f (x)=ax·g(x)(a>0,a≠1);②g(x)≠0;若+=,则a等于________.
4.(2010年北京朝阳模拟)已知函数f(x)=ax(a>0且a≠1),其反函数为f-1(x).若f(2)=9,则f-1()+f(1)的值是________.
5.(2010年山东青岛质检)已知f(x)=()x,若f(x)的图象关于直线x=1对称的图象对应的函数为g(x),则g(x)的表达式为________.
6.(2009年高考山东卷改编)函数y=的图象大致为________.
7.(2009年高考辽宁卷改编)已知函数f(x)满足:当x≥4时,f(x)=()x;当x<4时,f(x)=
f(x+1),则f(2+log23)=________.
8.(2009年高考湖南卷改编)设函数y=f(x)在(-∞,+∞)内有定义,对于给定的正数K,定义函数fK(x)=取函数f(x)=2-|x|,当K=时,函数fK(x)的单调递增区间为________.
9.函数y=2|x|的定义域为[a,b],值域为[1,16],当a变动时,函数b=g(a)的图象可以是________.
10.(2010年宁夏银川模拟)已知函数f(x)=a2x+2ax-1(a>0,且a≠1)在区间[-1,1]上的最大值为14,求实数a的值.
11.已知函数f(x)=.(1)求证:f(x)的图象关于点M(a,-1)对称;(2)若f(x)≥-2x在x≥a上恒成立,求实数a的取值范围.
12.(2008年高考江苏卷)若f1(x)=3|x-p1|,f2(x)=2·3|x-p2|,x∈R,p1、p2为常数,且
f(x)=(1)求f(x)=f1(x)对所有实数x成立的充要条件(用p1、p2表示);
(2)设a,b是两个实数,满足a0,且a≠1)的反函数,其图象经过点(,a),则f(x)=________.
2.(2009年高考全国卷Ⅱ)设a=log3π,b=log2,c=log3,则a、b、c的大小关系是________.
3.若函数f(x)=,则f(log43)=________.
4.如图所示,若函数f(x)=ax-1的图象经过点(4,2),则函数g(x)=loga的图象是________.
5.(原创题)已知函数f(x)=alog2x+blog3x+2,且f()=4,则f(2010)的值为________.
6.若f(x)=x2-x+b,且f(log2a)=b,log2f(a)=2(a>0且a≠1).
(1)求f(log2x)的最小值及相应x的值;(2)若f(log2x)>f(1)且log2f(x)0;④f()<.上述结论中正确结论的序号是________.
3.(2010年枣庄第一次质检)对任意实数a、b,定义运算“*”如下:
a*b=,则函数f(x)=log(3x-2)*log2x的值域为________.
4.已知函数y=f(x)与y=ex互为反函数,函数y=g(x)的图象与y=f(x)的图象关于x轴对称,若g(a)=1,则实数a的值为________.
5.已知函数f(x)满足f()=log2,则f(x)的解析式是________.
6.(2009年高考辽宁卷改编)若x1满足2x+2x=5,x2满足2x+2log2(x-1)=5,则x1+x2=________.
7.当x∈[n,n+1),(n∈N)时,f(x)=n-2,则方程f(x)=log2x根的个数是________.
8.(2010年福建厦门模拟)已知lga+lgb=0,则函数f(x)=ax与函数g(x)=-logbx的图象可能是________.
9.已知曲线C:x2+y2=9(x≥0,y≥0)与函数y=log3x及函数y=3x的图象分别交于点A(x1,y1),B(x2,y2),则x12+x22的值为________.
10.已知函数f(x)=lg(k∈R且k>0).
(1)求函数f(x)的定义域;(2)若函数f(x)在[10,+∞)上是单调增函数,求k的取值范围.
11.(2010年天津和平质检)已知f(x)=loga(a>0,a≠1).(1)求f(x)的定义域;
(2)判断f(x)的奇偶性并给予证明;(3)求使f(x)>0的x的取值范围.
12.已知函数f(x)满足f(logax)=(x-x-1),其中a>0且a≠1.
(1)对于函数f(x),当x∈(-1,1)时,f(1-m)+f(1-m2)<0,求实数m的集合;
(2)x∈(-∞,2)时,f(x)-4的值恒为负数,求a的取值范围.
第三节 幂函数与二次函数的性质
A组
1.若a>1且01的解集为________.
2.(2010年广东广州质检)下列图象中,表示y=x的是________.
3.(2010年江苏海门质检)若x∈(0,1),则下列结论正确的是__________.
①2x>x>lgx ②2x>lgx>x ③x>2x>lgx ④lgx>x>2x
4.(2010年东北三省模拟)函数f(x)=|4x-x2|-a恰有三个零点,则a=__________.
5.(原创题)方程x=logsin1x的实根个数是__________.
6.(2009年高考江苏卷)设a为实数,函数f(x)=2x2+(x-a)·|x-a|.
(1)若f(0)≥1,求a的取值范围;(2)求f(x)的最小值;
(3)设函数h(x)=f(x),x∈(a,+∞),直接写出(不需给出步骤)不等式h(x)≥1的解集.
B组
1.(2010年江苏无锡模拟)幂函数y=f(x)的图象经过点(-2,-),则满足f(x)=27的x的值是__________.
2.(2010年安徽蚌埠质检)已知幂函数f(x)=xα的部分对应值如下表:
x
1
f(x)
1
则不等式f(|x|)≤2的解集是__________.
3.(2010年广东江门质检)设k∈R,函数f(x)=F(x)=f(x)+kx,x∈R.当k=1时,F(x)的值域为__________.
4.设函数f(x)=若f(-4)=f(0),f(-2)=0,则关于x的不等式f(x)≤1的解集为__________.
5.(2009年高考天津卷改编)已知函数f(x)=若f(2-a2)>f(a),则实数a的取值范围是__________.
6.(2009年高考江西卷改编)设函数f(x)=(a<0)的定义域为D,若所有点(s,f(t))(s,t∈D)构成一个正方形区域,则a的值为__________.
7.(2010年辽宁沈阳模拟)已知函数f(x)=若f(0)=-2f(-1)=1,则函数g(x)=f(x)+x的零点的个数为__________.
8.设函数f(x)=x|x|+bx+c,给出下列四个命题:①c=0时,f(x)是奇函数;②b=0,c>0时,方程f(x)=0只有一个实根;③f(x)的图象关于(0,c)对称;④方程f(x)=0至多有两个实根.其中正确的命题是__________.
9.(2010年湖南长沙质检)对于区间[a,b]上有意义的两个函数f(x)与g(x),如果对于区间
[a,b]中的任意数x均有|f(x)-g(x)|≤1,则称函数f(x)与g(x)在区间[a,b]上是密切函数,[a,b]称为密切区间.若m(x)=x2-3x+4与n(x)=2x-3在某个区间上是“密切函数”,则它的一个密切区间可能是________.
①[3,4] ②[2,4] ③[2,3] ④[1,4]
10.设函数f(x)=x2+2bx+c(c2c>2b,求证:
(1)a>0且-3<<-;
(2)函数f(x)在区间(0,2)内至少有一个零点;
(3)设x1、x2是函数f(x)的两个零点,则≤|x1-x2|<.
12.已知函数f(x)=ax2+4x+b(a<0,a、b∈R),设关于x的方程f(x)=0的两实根为x1、x2,方程f(x)=x的两实根为α、β.
(1)若|α-β|=1,求a、b的关系式;
(2)若a、b均为负整数,且|α-β|=1,求f(x)的解析式;
(3)若α<1<β<2,求证:(x1+1)(x2+1)<7.
第四节 函数的图像特征
A组
1.命题甲:已知函数f(x)满足f(1+x)=f(1-x),则f(x)的图象关于直线x=1对称.命题乙:函数f(1+x)与函数f(1-x)的图象关于直线x=1对称.则甲、乙命题正确的是__________.
2.(2010年济南市高三模拟考试)函数y=·ax(a>1)的图象的基本形状是__________.
3.已知函数f(x)=()x-log3x,若x0是方程f(x)=0的解,且00时,
g(x)=log2x,则函数y=f(x)·g(x)的大致图象为__________.
5.某加油机接到指令,给附近空中一运输机加油.运输机的余油量为Q1(吨),加油机加油箱内余油Q2(吨),加油时间为t分钟,Q1、Q2与时间t的函数关系式的图象如右图.若运输机加完油后以原来的速度飞行需11小时到达目的地,问运输机的油料是否够用?________.
6.已知函数y=f(x)(x∈R)满足f(x+2)=f(x),且x∈(-1,1]时,f(x)=|x|,则y=f(x)与y=log7x的交点的个数为__________.
7.函数y=x(m,n∈Z,m≠0,|m|,|n|互质)图象如图所示,则下列结论正确的是__________.
①mn>0,m,n均为奇数
②mn<0,m,n一奇一偶
③mn<0,m,n均为奇数
④mn>0,m,n一奇一偶
8.(2009年高考福建卷改编)定义在R上的偶函数f(x)的部分图象如图所示,则在(-2,0)上,下列函数中与f(x)的单调性不同的是
①y=x2+1
②y=|x|+1
③y=
④y=
9.(2010年安徽合肥模拟)已知函数图象C′与C:y(x+a+1)=ax+a2+1关于直线y=x对称,且图象C′关于点(2,-3)对称,则a的值为__________.
10.作下列函数的图象:
(1)y=;
(2)y=|x-2|(x+1);
(3)y=;
(4)y=|log2x-1|;
(5)y=2|x-1|.
11.已知函数f(x)=-(a>0且a≠1).
(1)证明:函数y=f(x)的图象关于点(,-)对称;
(2)求f(-2)+f(-1)+f(0)+f(1)+f(2)+f(3)的值.
12.设函数f(x)=(x∈R,且a≠0,x≠).
(1)若a=,b=-,指出f(x)与g(x)=的图象变换关系以及函数f(x)的图象的对称中心;
(2)证明:若ab+1≠0,则f(x)的图象必关于直线y=x对称.
第四章 函数应用
A组
1.已知函数f(x)=则函数f(x)的零点个数为________.
2.根据表格中的数据,可以判定方程ex-x-2=0的一个根所在的区间为________.(填最恰当的一个)
x
-1
0
1
2
3
ex
0.37
1
2.72
7.39
20.09
x+2
1
2
3
4
5
3.偶函数f(x)在区间[0,a](a>0)上是单调函数,且f(0)·f(a)<0,则方程f(x)=0在区间[-a,a]内根的个数是__________.
4.(2009年高考浙江卷)某地区居民生活用电分为高峰和低谷两个时间段进行分时计价.该地区的电网销售电价表如下:
高峰时间段用电价格表
低谷时间段用电价格表
高峰月用电量
(单位:千瓦时)
高峰电价
(单位:元/千瓦时)
低谷月用电量
(单位:千瓦时)
低谷电价
(单位:元/千瓦时)
50及以下的部分
0.568
50及以下的部分
0.288
超过50至200的部分
0.598
超过50至200的部分
0.318
超过200的部分
0.668
超过200的部分
0.388
若某家庭5月份的高峰时间段用电量为200千瓦时,低谷时间段用电量为100千瓦时,则按这种计费方式该家庭本月应付的电费为________元(用数字作答).
5.(原创题)已知f(x)=|x|+|x-1|,若g(x)=f(x)-a的零点个数不为0,则a的最小值为________.
6.(2009年高考上海卷)有时可用函数f(x)=
描述学习某学科知识的掌握程度,其中x表示某学科知识的学习次数(x∈N*),f(x)表示对该学科知识的掌握程度,正实数a与学科知识有关.
(1)证明:当x≥7时,掌握程度的增长量f(x+1)-f(x)总是下降;
(2)根据经验,学科甲、乙、丙对应的a的取值区间分别为(115,121],(121,127],(127,133].当学习某学科知识6次时,掌握程度是85%,请确定相应的学科.
B组
1.(2010年浙江温州质检)某学校开展研究性学习活动,一组同学获得了下面的一组试验数据:
x
1.99
3
4
5.1
6.12
y
1.5
4.04
7.5
12
18.01
现准备用下列四个函数中的一个近似地表示这些数据的规律,其中最接近的一个是________
①y=2x-2 ②y=()x ③y=log2x ④y=(x2-1)
2.(2010年安徽省江南十校模拟)函数f(x)=2x+x-7的零点所在的区间是________.
①(0,1) ②(1,2) ③(2,3) ④(3,4)
3.已知函数f(x)=x+log2x,则f(x)在[,2]内的零点的个数是______.
4.(2010年珠海质检)某种细胞在培养过程中正常情况下,时刻t(单位:分钟)与细胞数n
(单位:个)的部分数据如下:
t
0
20
60
140
n
1
2
8
128
根据表中数据,推测繁殖到1000个细胞时的时刻t最接近于________分钟.
5.某化工厂打算投入一条新的生产线,但需要经环保部门审批同意方可投入生产.已知该生产线连续生产n年的累计产量为f(n)=n(n+1)(2n+1)吨,但如果年产量超过150吨,将会给环境造成危害.为保护环境,环保部门应给该厂这条生产线拟定最长的生产期限是________年.
6.(2010年苏、锡、常、镇四市调研)某市出租车收费标准如下:起步价为8元,起步里程为3 km(不超过3 km按起步价付费);超过3 km但不超过8 km时,超过部分按每千米2.15元收费;超过8 km时,超过部分按每千米2.85元收费,另每次乘坐需付燃油附加费1元.现某人乘坐一次出租车付费22.6元,则此次出租车行驶了________km.
7.(2010年绍兴第一次质检)一位设计师在边长为3的正方形ABCD中设计图案,他分别以A、B、C、D为圆心,以b(00,则α是第__________象限的角.
4.函数y=++的值域为________.
5.(原创题)若一个α角的终边上有一点P(-4,a),且sinα·cosα=,则a的值为________.
6.已知角α的终边上的一点P的坐标为(-,y)(y≠0),且sinα=y,求cosα,tanα的值.
B组
1.已知角α的终边过点P(a,|a|),且a≠0,则sinα的值为________.
2.已知扇形的周长为6 cm,面积是2 cm2,则扇形的圆心角的弧度数是______________.
3.如果一扇形的圆心角为120°,半径等于 10 cm,则扇形的面积为________.
4.若角θ的终边与168°角的终边相同,则在0°~360°内终边与角的终边相同的角的集合为__________.
5.若α=k·180°+45°(k∈Z),则α是第________象限.
6.设角α的终边经过点P(-6a,-8a)(a≠0),则sinα-cosα的值是________.
7.(2010年北京东城区质检)若点A(x,y)是300°角终边上异于原点的一点,则的值为________.
8.(2010年深圳调研)已知点P(sin,cos)落在角θ的终边上,且θ∈[0,2π),则θ的值为________.
9.已知角α的始边在x轴的非负半轴上,终边在直线y=kx上,若sinα=,且cosα<0,则k的值为________.
10.已知一扇形的中心角是α,所在圆的半径是R.若α=60°,R=10 cm,求扇形的弧长及该弧所在的弓形面积.
11.扇形AOB的周长为8 cm.
(1)若这个扇形的面积为3 cm2,求圆心角的大小;
(2)求这个扇形的面积取得最大值时圆心角的大小和弦长AB.
12.(1)角α的终边上一点P(4t,-3t)(t≠0),求2sinα+cosα的值;
(2)已知角β的终边在直线y=x上,用三角函数定义求sinβ的值.
第二节 正弦函数和余弦函数的定义及诱导公式
A组
1.若cosα=-,α∈(,π),则tanα=________.
2.(2009年高考北京卷)若sinθ=-,tanθ>0,则cosθ=________.
3.若sin(+α)=,则cos(-α)=________.
4.(2010年合肥质检)已知sinx=2cosx,则=______.
5.(原创题)若cos2θ+cosθ=0,则sin2θ+sinθ=________.
6.已知sin(π-α)cos(-8π-α)=,且α∈(,),求cosα,sinα的值.
B组
1.已知sinx=2cosx,则sin2x+1=________.
2.(2010年南京调研)cos=________.
3.(2010年西安调研)已知sinα=,且α∈(,π),那么的值等于________.
4.(2010年南昌质检)若tanα=2,则+cos2α=_____________.
5.(2010年苏州调研)已知tanx=sin(x+),则sinx=______________.
6.若θ∈[0,π),且cosθ(sinθ+cosθ)=1,则θ=________.
7.已知sin(α+)=,则cos(α+)的值等于________.
8.(2008年高考浙江卷改编)若cosα+2sinα=-,则tanα=________.
9.已知f(α)=,则f(-)的值为________.
10.求sin(2nπ+)·cos(nπ+)(n∈Z)的值.
11.在△ABC中,若sin(2π-A)=-sin(π-B),cosA=-cos(π-B),求△ABC的三内角.
12.已知向量a=(,1),向量b=(sinα-m,cosα).
(1)若a∥b,且α∈[0,2π),将m表示为α的函数,并求m的最小值及相应的α值;
(2)若a⊥b,且m=0,求的值.
第三节 正弦函数与余弦函数的图像与性质
A组
1.(2009年高考四川卷改编)已知函数f(x)=sin(x-)(x∈R),下面结论错误的是________.
①函数f(x)的最小正周期为2π
②函数f(x)在区间[0,]上是增函数
③函数f(x)的图象关于直线x=0对称
④函数f(x)是奇函数
2.(2009年高考广东卷改编)函数y=2cos2(x-)-1是________.
①最小正周期为π的奇函数 ②最小正周期为π的偶函数 ③最小正周期为的奇函数 ④最小正周期为的偶函数
3.(2009年高考江西卷改编)若函数f(x)=(1+tanx)cosx,0≤x<,则f(x)的最大值为________.
4.已知函数f(x)=asin2x+cos2x(a∈R)图象的一条对称轴方程为x=,则a的值为________.
5.(原创题)设f(x)=Asin(ωx+φ)(A>0,ω>0)的图象关于直线x=对称,它的最小正周期是π,则f(x)图象上的一个对称中心是________(写出一个即可).
6.(2010年宁波调研)设函数f(x)=cos2x+sinxcosx-.
(1)求函数f(x)的最小正周期T,并求出函数f(x)的单调递增区间;
(2)求在[0,3π)内使f(x)取到最大值的所有x的和.
B组
1.函数f(x)=sin(x+)+sinx的图象相邻的两条对称轴之间的距离是________.
2.(2010年天津河西区质检)给定性质:a最小正周期为π;b图象关于直线x=对称.则下列四个函数中,同时具有性质ab的是________.
①y=sin(+) ②y=sin(2x+) ③y=sin|x| ④y=sin(2x-)
3.(2009年高考全国卷Ⅰ改编)若0)在[-,]上单调递增,则ω的最大值为________.
6.(2010年南京调研)设函数y=2sin(2x+)的图象关于点P(x0,0)成中心对称,若x0∈[-,0],则x0=________.
7.已知函数y=Asin(ωx+φ)+m的最大值为4,最小值为0,最小正周期为,直线x=是其图象的一条对称轴,则下面各式中符合条件的解析式是________.
①y=4sin(4x+) ②y=2sin(2x+)+2
③y=2sin(4x+)+2 ④y=2sin(4x+)+2
8.有一种波,其波形为函数y=sinx的图象,若在区间[0,t]上至少有2个波峰(图象的最高点),则正整数t的最小值是________.
9.(2009年高考安徽卷改编)已知函数f(x)=sinωx+cosωx(ω>0),y=f(x)的图象与直线y=2的两个相邻交点的距离等于π,则f(x)的单调递增区间是________.
10.已知向量a=(2sinωx,cos2ωx),向量b=(cosωx,2),其中ω>0,函数f(x)=a·b,若f(x)图象的相邻两对称轴间的距离为π.
(1)求f(x)的解析式;
(2)若对任意实数x∈[,],恒有|f(x)-m|<2成立,求实数m的取值范围.
11.设函数f(x)=a·b,其中向量a=(2cosx,1),b=(cosx,sin2x+m).
(1)求函数f(x)的最小正周期和在[0,π]上的单调递增区间;
(2)当x∈[0,]时,f(x)的最大值为4,求m的值.
12.已知函数f(x)=sinωx-2sin2+m(ω>0)的最小正周期为3π,且当x∈[0,π]时,函数 f(x)的最小值为0.
(1)求函数f(x)的表达式;
(2)在△ABC中,若f(C)=1,且2sin2B=cosB+cos(A-C),求sinA的值.
第四节 函数f(x)=Asin(ωx+φ)的图像
A组
1.(2009年高考浙江卷改编)已知a是实数,则函数f(x)=1+asinax的图象不可能是________.
2.(2009年高考湖南卷改编)将函数y=sinx的图象向左平移φ(0≤φ<2π)个单位后,得到函数y=sin(x-)的图象,则φ等于________.
3.将函数f(x)=sinx-cosx的图象向右平移φ(φ>0)个单位,所得图象对应的函数为奇函数,则φ的最小值为________.
4.如图是函数f(x)=Asin(ωx+φ)(A>0,ω>0,-π<φ<π),x∈R的部分图象,则下列命题中,正确命题的序号为________.
①函数f(x)的最小正周期为;
②函数f(x)的振幅为2;
③函数f(x)的一条对称轴方程为x=π;
④函数f(x)的单调递增区间为[,π];
⑤函数的解析式为f(x)=sin(2x-π).
5.(原创题)已知函数f(x)=sinωx+cosωx,如果存在实数x1,使得对任意的实数x,都有f(x1)≤f(x)≤f(x1+2010)成立,则ω的最小值为________.
6.(2010年苏北四市质检)已知函数f(x)=sin2ωx+sinωx·sin(ωx+)+2cos2ωx,x∈R(ω>0),在y轴右侧的第一个最高点的横坐标为.(1)求ω;(2)若将函数f(x)的图象向右平移个单位后,再将得到的图象上各点横坐标伸长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求函数g(x)的最大值及单调递减区间.
B组
1.(2009年高考宁夏、海南卷)已知函数y=sin(ωx+φ)(ω>0,-π≤φ<π)的图象如图所示,则φ=________.
(第1题) (第2题) (第4题)
2.(2010年南京调研)已知函数y=sin(ωx+φ)(ω>0,|φ|<π)的图象如图所示,则φ=________.
3.(2009年高考天津卷改编)已知函数f(x)=sin(ωx+)(x∈R,ω>0)的最小正周期为π,为了得到函数g(x)=cosωx的图象,只要将y=f(x)的图象________________.
4.(2009年高考辽宁卷改编)已知函数f(x)=Acos(ωx+φ) 的图象如图所示,f()=-,则f(0)=________.
5.将函数y=sin(2x+)的图象向________平移________个单位长度后所得的图象关于点(-,0)中心对称.
6.(2010年深圳调研)定义行列式运算:=a1a4-a2a3,将函数f(x)=的图象向左平移m个单位(m>0),若所得图象对应的函数为偶函数,则m的最小值是________.
7.(2009年高考全国卷Ⅱ改编)若将函数y=tan(ωx+)(ω>0)的图象向右平移个单位长度后,与函数y=tan(ωx+)的图象重合,则ω的最小值为________.
8.给出三个命题:①函数y=|sin(2x+)|的最小正周期是;②函数y=sin(x-)在区间[π,]上单调递增;③x=是函数y=sin(2x+)的图象的一条对称轴.其中真命题的个数是________.
9.(2009年高考上海卷)当0≤x≤1时,不等式sin≥kx恒成立,则实数k的取值范围是________.
10.(2009年高考重庆卷)设函数f(x)=(sinωx+cosωx)2+2cos2ωx(ω>0)的最小正周期为.(1)求ω的值;(2)若函数y=g(x)的图象是由y=f(x)的图象向右平移
个单位长度得到,求y=g(x)的单调增区间.
11.(2009年高考陕西卷)已知函数f(x)=Asin(ωx+φ),x∈R(其中A>0,ω>0,0<φ<)的周期为π,且图象上一个最低点为M(,-2).(1)求f(x)的解析式;(2)当x∈[0,]时,求f(x)的最值.
12.(2009年高考福建卷)已知函数f(x)=sin(ωx+φ),其中ω>0,|φ|<.
(1)若coscosφ-sinsinφ=0,求φ的值;
(2)在(1)的条件下,若函数f(x)的图象的相邻两条对称轴之间的距离等于,求函数f(x)的解析式;并求最小正实数m,使得函数f(x)的图象向左平移m个单位后所对应的函数是偶函数.
第六章 三角恒等变形
第一节 同角三角函数的基本关系
A组
1.已知sinα=,sin(α-β)=-,α、β均为锐角,则β等于________.
2.已知0<α<<β<π,cosα=,sin(α+β)=-,则cosβ的值为________.
3.如果tanα、tanβ是方程x2-3x-3=0的两根,则=________.
4.(2008年高考山东卷改编)已知cos(α-)+sinα=,则sin(α+)的值是________.
5.(原创题)定义运算ab=a2-ab-b2,则sincos=________.
6.已知α∈(,π),且sin+cos=.
(1)求cosα的值;
(2)若sin(α-β)=-,β∈(,π),求cosβ的值.
B组
1.·的值为________.
2.已知cos(+x)=,则的值为________.
3.已知cos(α+)=sin(α-),则tanα=________.
4.设α∈(,),β∈(0,),cos(α-)=,sin(+β)=,则sin(α+β)=________.
5.已知cosα=,cos(α+β)=-,且α,β∈(0,),则cos(α-β)的值等于________.
6.已知角α在第一象限,且cosα=,则=________.
7.已知a=(cos2α,sinα),b=(1,2sinα-1),α∈(,π),若a·b=,则tan(α+)的值为________.
8 . 的值为______.
9.已知角α的终边经过点A(-1,),则的值等于________.
10.求值:·cos10°+sin10°tan70°-2cos40°.
11.已知向量m=(2cos,1),n=(sin,1)(x∈R),设函数f(x)=m·n-1.
(1)求函数f(x)的值域;
(2)已知锐角△ABC的三个内角分别为A,B,C,若f(A)=,f(B)=,求f(C)的值.
12.(2010年南京调研)已知:0<α<<β<π,cos(β-)=,sin(α+β)=.
(1)求sin2β的值;
(2)求cos(α+)的值.
第二节 两角和与差及二倍角的三角函数
A组
1.若sinα=,α∈(-,),则cos(α+)=________.
2.已知π<θ<π,则 =________.
3.(2010年南京市调研)计算:=________.
4.(2009年高考上海卷)函数y=2cos2x+sin2x的最小值是__________________.
5.(原创题)函数f(x)=(sin2x+)(cos2x+)的最小值是________.
6.已知角α∈(,),且(4cosα-3sinα)(2cosα-3sinα)=0.
(1)求tan(α+)的值;(2)求cos(-2α)的值.
B组
1.(2010年苏、锡、常、镇四市调研)若tan(α+β)=,tan(β-)=,
则tan(α+)=________.
2.(2009年高考陕西卷改编)若3sinα+cosα=0,则的值为________.
3.设a=sin14°+cos14°,b=sin16°+cos16°,c=,则a、b、c的大小关系是________.
4.+2的化简结果是________.
5.若tanα+=,α∈(,),则sin(2α+)的值为_________.
6.若函数f(x)=sin2x-2sin2x·sin2x(x∈R),则f(x)的最小正周期为________.
7.(2010年无锡质检)的值为________.
8.向量a=(cos10°,sin10°),b=(cos70°,sin70°),|a-2b
|=_________________.
9.(2010年江苏省南通市调研)已知=1,tan(β-α)=-,则tan(β-2α)=________.
10.已知tanα=2.求(1)tan(α+)的值;(2)的值.
11.如图,点A,B是单位圆上的两点,A,B两点分别在第一、二象限,点C是圆与x轴正半轴的交点,△AOB是正三角形,若点A的坐标为(,),记∠COA=α.
(1)求的值;(2)求|BC|2的值.
12.(2009年高考江西卷)△ABC中,A,B,C所对的边分别为a,b,c,tanC=,sin(B-A)=cosC.
(1)求角A,C.
(2)若S△ABC=3+,求a,c.
第七章 解三角形
第一节 正弦定理与余弦定理
1.(2008·陕西理,3)△ABC的内角A、B、C的对边分别为a、b、c,若c=,b=,B=120°,则a等于 ( )
A. B.2 C. D.
2.(2008·福建理,10)在△ABC中,角A、B、C的对边分别为a、b、c,若(a2+c2-b2)tanB=ac,则角B的值为( )
A. B. C.或 D.或
3.下列判断中正确的是 ( )
A.△ABC中,a=7,b=14,A=30°,有两解
B.△ABC中,a=30,b=25,A=150°,有一解
C.△ABC中,a=6,b=9,A=45°,有两解
D.△ABC中,b=9,c=10,B=60°,无解
4. 在△ABC中,若2cosBsinA=sinC,则△ABC一定是 ( )
A.等腰直角三角形 B.等腰三角形 C.直角三角形 D.等边三角形
5. 在△ABC中,A=120°,AB=5,BC=7,则的值为 ( )
A. B. C. D.
6.△ABC中,若a4+b4+c4=2c2(a2+b2),则∠C的度数是 ( )
A.60° B.45°或135° C.120° D.30°
7.在△ABC中,角A,B,C所对的边分别为a,b,c,若a=1,b=,c=,则B= .
8. 在△ABC中,A=60°,AB=5,BC=7,则△ABC的面积为 .
9. (2008·浙江理,13)在△ABC中,角A、B、C所对的边分别为a、b、c.
若(b-c)cosA=acosC,则cosA= .
10. 在△ABC中,已知a=,b=,B=45°,求A、C和c.
11. 在△ABC中,a、b、c分别是角A,B,C的对边,且=-.
(1)求角B的大小;(2)若b=,a+c=4,求△ABC的面积.
12. 在△ABC中,a、b、c分别表示三个内角A、B、C的对边,如果(a2+b2)sin(A-B)=(a2-b2)sin(A+B),判断三角形的形状.
13. 已知△ABC中,三个内角A,B,C的对边分别为a,b,c,若△ABC的面积为S,且2S=(a+b)2-c2,求tanC的值.
14. 已知△ABC的三个内角A、B、C的对边分别为a、b、c,若a、b、c成等差数列,且2cos2B-8cosB+5=0,求角B的大小并判断△ABC的形状.
15. (2008·广东五校联考)在△ABC中,角A、B、C的对边分别为a、b、c,已知a+b=5,c=,且4sin2-cos2C=.
(1)求角C的大小;
(2)求△ABC的面积.
第二节 正弦定理、余弦定理的应用
1.从A处望B处的仰角为,从B处望A处的俯角为,则的关系为 ( )
A.> B.= C.+=90° D.+=180°
2.已知A、B两地的距离为10 km,B、C两地的距离为20 km,现测得∠ABC=
120°,则A、C两地的距离为 ( )
A.10 km B. km C. km D.10 km
3.为测量某塔AB的高度,在一幢与塔AB相距20 m的楼顶处测得塔顶A的仰角为30°,测得塔基B的俯角为45°,那么塔AB的高度是 ( )
A. m B. m C. m D.30 m
4.如图,位于港口O正东20海里B处的渔船回港时出现故障.位于港口南偏西30°,距港口10海里C处的拖轮接到海事部门营救信息后以30海里/小时的速度沿直线CB去营救渔船,则拖轮到达B处需要________小时.
5.(2010年南京市高中联考)如图,海岸线上有相距5海里的两座灯塔A,B,灯塔B位于灯塔A的正南方向.海上停泊着两艘轮船,甲船位于灯塔A的北偏西75°,与A相距3海里的D处;乙船位于灯塔B的北偏西60°方向,与B相距5海里的C处.则两艘轮船之间的距离为________海里.
6.(2010年宁波十校联考)一船向正北方向匀速行驶,看见正西方向两座相距10海里的灯塔恰好与该船在同一直线上,继续航行半小时后,看见其中一座灯塔在南偏西60°方向上,另一灯塔在南偏西75°方向上,则该船的速度是________海里/小时.
7.如图,某住宅小区的平面图呈圆心角为120°的扇形AOB,C是该小区的一个出入口,且小区里有一条平行于AO的小路CD.已知某人从O沿OD走到D用了2分钟,从D沿着DC走到C用了3分钟.若此人步行的速度为每分钟50米,则该扇形的半径为________米.
8.(原创题)在Rt△ABC中,斜边AB=2,内切圆的半径为r,则r的最大值为________.
9.(2009年高考辽宁卷)如图,A、B、C、D都在同一个与水平面垂直的平面内,B、D为两岛上的两座灯塔的塔顶,测量船于水面A处测得B点和D点的仰角分别为75°、30°,于水面C处测得B点和D点的仰角均为60°,AC=0.1 km.试探究图中B、D间距离与另外哪两点间距离相等,然后求B、D的距离(计算结果精确到0.01 km,≈1.414,≈2.449).
第八章 数列
1.已知数列满足条件,且,设,那么数列的通项公式是
2.x=是a、x、b成等比数列的( )
A.充分非必要条件B.必要非充分条件C.充要条件 D.既非充分又非必要条件
3.已知数列{an}的前n项和Sn=an-1(a),则数列{an}( )
A.一定是等差 B.一定是等比 C.或是等差或是等比 D.既非等差又非等比
4.弹子跳棋共有60颗大小的球形弹子,现在棋盘上将它叠成正四面体形球垛,使剩下的弹子尽可能的少,那么剩余的弹子有 ( )
A. 0颗 B.4颗 C.5颗 D.11颗
5.某学生家长为缴纳该学生上大学时的教育费,于2003年8月20号从银行贷款a元,为还清这笔贷款,该家长从2004年起每年的8月20号便去银行偿还确定的金额,计划恰好在贷款的m年后还清,若银行按年利息为p的复利计息(复利:即将一年后的贷款利息也纳入本金计算新的利息),则该学生家长每年的偿还金额是 ( )
A. B. C. D.
6.已知为等比数列,,又第项至第项的和为720,则 ,
7.数列对任意都满足,且,
则
8.已知函数,那么
9.一个项数为偶数的等比数列,首项是1,且所有奇数项之和是85,所有偶数项之和是170,则此数列共有_________项
10.在各项为正数的等比数列中,已知,且前项的和等于它的前项中偶数项之和的11倍,则数列的通项公式
_____________
11.已知数列中,,那么的值为 。
12.等差数列中,,且,则中最大项为 。
13.已知一个等差数列前五项的和是120,后五项的和是180,又各项之和是
360,则此数列共有 项。
14.设,利用课本中推导等差数列前n项和的公式的方法,可求得: 的值为
15.已知数列的通项,前n项和为,则= 。
16.数列前n项的和等于 。
17.已知数列是首项为,公差为的等差数列,若数列是等比数列,则其公比为( )
18.已知在数列中,+d (>0).
(1)若求并猜测;
(2)若是等比数列,且是等差数列,求满足的条件.
19.已知一个等差数列的前10项的和是310,前20项的和是1220,试求其前项和。
第九章 平面向量
1.已知三个向量a=(cos,sin),b=(cos,sin),c=,sin),满足,则a与b的夹角为
2.下列命题:
(1)若a与b为非零向量,且a∥b时,则a—b必与a或b中之一的方向相同;
(2)若e为单位向量,且a∥e,则a=|a|e;
(3)a·a·a=|a|3
(4)若a与b共线,又b与c共线,则a与c必共线
(5)若平面内四个点A、B、C、D则必有AC+BD=BC+AD
正确的命题个数为( )
A、1 B、2 C、3 D、0
3.若o为平行四边形ABCD的中心,=41, 等于( )
A. B. C. D.
4.若,且(),则实数的值为____________.
5.已知,与的夹角为,则在上的投影为 。
6.在直角坐标平面上,向量,向量,两向量在直线上的正射影长度相等,则直线的斜率为
7.设平面向量=(-2,1),=(1,),若与的夹角为钝角,则的取值范围是 。
8.已知向量,则向量的夹角范围是 。
9.将函数的图象按向量 平移后得到的图象,给出以下四个命题:
①的坐标可以是; ②的坐标可以是和;
③的坐标可以是; ④的坐标可以有无数种情况。
上述说法正确的是 。
10.已知中,,则与的夹角为 。
11.若△ABC三边长AB=5,BC=7,AC=8,则等于 。
12.已知的夹角为120°,且,,当时,k= .
13.已知A(3,y),B(,2),C(6,)三点共线,则y=_________.
14. 若=(1,2),=(,2), k为何值时:
(1)k+与-3垂直;(2)k+与 -3平行?
15. 已知||=4,||=3,(2-3)·(2+)=61,求:(i)与的夹角θ;
(ii) .
16. 已知的顶点坐标分别为A(1,2),B(2,3),C(-2,5),求.
17. 设=(sinx-1,cosx-1),=(,).
(1)若为单位向量,求x的值;
(2)设f(x)=·,则函数y=f(x)的图象是由y=sinx的图象如何平移得到?
18.已知,且.
(i)求 及; (ii)求函数的最小值.
第十章 算法
第一节 程序框图
A组
1.(2009年高考福建卷改编)阅读如图所示的程序框图,运行相应的程序,输出的结果是________.
2.(2009年高考宁夏、海南卷改编)如果执行如图的程序框图,输入x=-2,h=0.5,那么输出的各个数的和等于________.
3.(2009年高考山东卷改编)执行下面的程序框图,输出的T=________.
(第1题) (第2题) (第3题)
4.(2010年南京市高三调研)阅读下面的流程图,若输入a=6,b=1,则输出的结果是________.
(第4题) (第5题) (第6题)
5.(2010年苏、锡、常、镇四市高三调研)阅读如图所示的程序框图,若输入的n是100,则输出的变量S的值是多少?
6.(原创题)已知如图所示的程序框图(未完成),设当箭头a指向①时,输出的结果为S=m,当箭头a指向②时,输出的结果为S=n,求m+n的值.
B组
1.(2010年温州调研)如图是一算法的程序框图,若此程序运行结果为s=720,则在判断框中应填入的关于k的判断条件是__________.
(第1题) (第2题) (第3题)
2.若R=8,则下列流程图的运行结果为______.
3.给出一个如图所示的程序框图,若要使输入的x的值与输出的y的值相等,则x的可能值的个数为________.
4.如图,该程序运行后输出的结果为________.
5.已知流程图如图所示,该程序运行后,为使输出的b值为16,则循环体的判断框内①处应填___________.
(第4题) (第5题) (第6题)
6.按如图所示的程序框图运行后,输出的结果是63,则判断框中的整数M的值是________.
7.(2009年高考广东卷改编)某篮球队6名主力队员在最近三场比赛中投进的三分球个数如下表所示:
队员i
1
2
3
4
5
6
三分球个数
a1
a2
a3
a4
a5
a6
下图是统计该6名队员在最近三场比赛中投进的三分球总数的程序框图,则图中判断框应填___________,输出的s=___________.
(注:框图中的赋值符号“←”也可以写成“=”或“:=”)
(第7题) (第8题)
8.(2009年高考上海卷)某算法的程序框图如图所示,则输出量y与输入量x满足的关系式是________.
9.某流程如图所示,现输入如下四个函数
①f(x)=x2;②f(x)=;③f(x)=lnx;④f(x)=sinx.
则输入函数与输出函数为同一函数的是 .
(第9题) (第10题)
10.如图所示的算法中,令a=tanθ,b=sinθ,c=cosθ,若在集合中,给θ取一个值,输出的结果是sinθ,求θ值所在的范围.
11.画出计算1+++…++值的一个算法的流程图.
12.到银行办理个人异地汇款(不超过100万元)时,银行要收取一定的手续费.汇款额不超过100元,收取1元手续费;超过100元但不超过5000元,按汇款额的1%收取;超过5000元,一律收取50元手续费.设计算法求汇款额为x元时,银行收取的手续费y元,只画出流程图.
第二节 程序语句
A组
1.(2010年徐州调研)如图,给出一个算法的伪代码,
T←1
I←3
While I<50
T←T+I
I←I+2
End While
Print T
则f(-3)+f(2)=________.
Input x
If x<0 Then
y←(x+1)(x-1)
Else
y←(x-1)2
End If
Print y
End
Input x
If x≤0 Then
f(x)←4x
Else
f(x)←2x
End If
Print f(x)
(第1题) (第2题) (第3题)
2.输入x=5,运行下面的程序之后得到的y等于________.
3.(2010年泰州质检)根据如图所示的伪代码,可知输出的结果T为________.
4.(2009年高考安徽卷改编)程序框图(即算法流程图)如图所示,其输出结果是________.
Input n
S←0
I←1
While________
S←S+I
I←I+1
Wend
Print “S=”;S
End
(第4题) (第5题) (第6题)
5.(原创题)编写程序求S=1+2+3+…+n的和(n由键盘输入),程序如图,则横线上应填________.
6.(2009年高考江苏卷改编)下图是一个算法的流程图,求最后输出的W的值.
n←5
S←0
While S<15
S←S+n
n←n-1
End While
Print n
B组
1.右面程序执行后输出的结果是________.
2.下列程序的功能是:判断任意输入的数x是否是正数,若是,输出它的平方值;若不是,输出它的相反数.则填入的条件应该是________.
x←Input(“x=”)
If________
y←-x;
Else
y←x2
End If
Print y
3.程序如下:
a←Input(“a=”)
b←Input(“b=”)
c←Input(“c=”)
a←b
b←c
c←a
Print a,b,c
若输入10,20,30,则输出结果为________.
4.(2010年南通调研)程序如下:
t←1
i←2
While i≤4
t←t×i
i←i+1
End While
Print t
以上程序输出的结果是________.
5.有下面算法:
p←1
For k From 1 To 10 Step 3
p←p+2×k-6
End For
Print p
则运行后输出的结果是________.
6.(2010年南京第一次调研)根据如图所示的伪代码,可知输出的结果I为________.
S←1
I←1
While S<5
S←S×
I←I+1
End While
Print I
7.现欲求1+++…+的和(其中n的值由键盘输入),已给出了其程序框图,请将其补充完整并设计出程序.
8.已知函数y=x2+2x(x∈[-10,10],x∈Z),编写程序,求该函数的最大值.
第十一章 概率
第一节 古典概型
A组
1.某产品分甲、乙、丙三级,其中乙、丙两级均属次品,在正常生产情况下,出现乙级品和丙级品的概率分别是5%和3%,则抽验一只是正品(甲级品)的概率为________.
2.某射手在一次射击中,射中10环,9环,8环的概率分别是0.20,0.30,0.10,则此射手在一次射击中不够8环的概率为________.
3.从甲、乙、丙、丁四人中任选两名代表,甲被选中的概率为________.
4.(2010年佛山第二次质检)从一个信箱中任取一封信,记一封信的重量为ξ(单位:克),如果P(ξ<10)=0.3,P(10≤ξ≤30)=0.4,则P(ξ>30)=________.
5.某种电子元件在某一时刻是否接通的可能性是相同的,有3个这样的电子元件,则出现至少有一个接通的概率为________.
6.(2010年南京调研)某学校的篮球队、羽毛球队、乒乓球队各有10名队员,某些队员不止参加了一支球队,具体情况如图所示,现从中随机抽取一名队员,求:
(1)该队员只属于一支球队的概率;
(2)该队员最多属于两支球队的概率.
B组
1.(2009年高考安徽卷)从长度分别为2、3、4、5的四条线段中任意取出三条,则以这三条线段为边可以构成三角形的概率是________.
2.甲射手击中靶心的概率为,乙射手击中靶心的概率为,甲、乙两人各射击一次,那么,甲、乙不全击中靶心的概率为________.
3.口袋内装有一些大小相同的红球、白球和黑球,从中摸出1个球,摸出红球的概率是0.42,摸出白球的概率是0.28,那么摸出黑球的概率是________.
4.甲、乙两人各写一张贺年卡随意送给丙、丁两人中的一人,则甲、乙将贺年卡送给同一人的概率是________.
5.(2008年高考江苏卷)若将一颗质地均匀的骰子(一种各面上分别标有1,2,3,4,5,6个点的正方体玩具)先后抛掷2次,则出现向上的点数之和为4的概率是________.
6.有两个质地均匀、大小相同的正四面体玩具,每个玩具的各面上分别写有数字1、2、3、4,把两个玩具各抛掷一次,斜向上的面写有的数字之和能被5整除的概率为________.
7.有一个奇数列1,3,5,7,9,…,现在进行如下分组,第一组有1个数为1,第二组有2个数为3、5,第三组有3个数为7、9、11,…
,依此类推,则从第十组中随机抽取一个数恰为3的倍数的概率为________.
8.先后抛掷两枚均匀的正方体骰子(它们的六个面分别标有点数1、2、3、4、5、6),骰子朝上的面的点数分别为x、y,则满足log2xy=1的概率为________.
9.(2010年江苏宿迁模拟)将一枚骰子抛掷两次,若先后出现的点数分别为b、c则方程x2+bx+c=0有实根的概率为____________.
10.如图,四边形ABCD被两条对角线分成四个小三角形,若 每个小三角形用4种不同颜色中的任一种涂染,求出现相邻三角形均不同色的概率.
11.在数学考试中,小明的成绩在90分及以上的概率是0.18,在80~89分的概率是0.51,在70~79分的概率是0.15,在60~69分的概率是0.09,计算小明在数学考试中取得80分及以上成绩的概率和小明考试不及格(低于60分)的概率.
12.盒中有6只灯泡,其中2只次品,4只正品,有放回地从中任取2次,每次只取1只,试求下列事件的概率:
(1)取到的2只都是次品;
(2)取到的2只中正品、次品各1只;
(3)取到的2只中至少有1只正品.
第二节 概率的应用
A组
1.在一个袋子中装有分别标注数字1,2,3,4,5的五个小球,这些小球除标注的数字外完全相同.现从中随机取出2个小球,则取出的小球标注的数字之和为3或6的概率是________.
2.已知k∈Z,=(k,1),=(2,4),若|A|≤4,则△ABC是直角三角形的概率为________.
3.(2010年南京调研)甲盒子里装有分别标有数字1,2,4,7的4张卡片,乙盒子里装有分别标有数字1,4的2张卡片.若从两个盒子中各随机地取出1张卡片,则2张卡片上的数字之和为奇数的概率是________.
4.(2009年高考江苏卷)现有5根竹竿,它们的长度(单位:m)分别为2.5,2.6,2.7,2.8,2.9,若从中一次随机抽取2根竹竿,则它们的长度恰好相差0.3 m的概率为________.
5.(原创题)连掷两次骰子分别得到点数m,n,向量a=(m,n),b=(-1,1),若在△ABC中,A与a同向,C与b反向,则∠ABC是钝角的概率是________.
6.一个袋子中有红、白、蓝三种颜色的球共24个,除颜色外其他特征完全相同,已知蓝色球3个.若从袋子中随机取出1个球,取到红色球的概率是.
(1)求红色球的个数;
(2)若将这三种颜色的球分别进行编号,并将1号红色球,1号白色球,2号蓝色球和3号蓝色球这四个球装入另一个袋子中,甲乙两人先后从这个袋子中各取一个球(甲先取,取出的球不放回),求甲取出的球的编号比乙大的概率.
B组
1.(2009年高考浙江卷)有20张卡片,每张卡片上分别标有两个连续的自然数k,k+1,其中k=0,1,2,…,19.从这20张卡片中任取一张,记事件“该卡片上两个数的各位数字之和(例如:若取到标有9,10的卡片,则卡片上两个数的各位数字之和为9+1+0=10)不小于14”为A,则P(A)=________.
2.用黑白两种颜色的正方形地砖依照下图的规律拼成若干图形,则按此规律第100个图形中有白色地砖________块;现将一粒豆子随机撒在第100个图形中,则豆子落在白色地砖上 的概率是________.
3.设集合A={1,2},B={1,2,3},分别从集合A和B中随机取一个数a和b,确定平面上的一个点P(a,b),记“点P(a,b)落在直线x+y=n上”为事件Cn(2≤n≤5,n∈N),若事件Cn的概率最大,则n的所有可能值为________.
4.先后从分别标有数字1,2,3,4的4个大小、形状完全相同的球中,有放回地随机抽取2个球,则抽到的2个球的标号之和不大于5的概率等于________.
5.把一颗骰子投掷两次,观察出现的点数,并记第一次出现的点数为a,第二次出现的点数为b,向量m=(a,b),n=(1,-2),则向量m与向量n垂直的概率是________.
6.(2010年南京高三调研)如图,将体积为27 cm3的正方体木块表面涂上蓝色,然后锯成体积为1 cm3小正方体,从中任取一块,则这一块恰有两面涂有蓝色的概率是 .
7.集合A={2,4,6,8,10},B={1,3,5,7,9},在A中任取一元素m和在B中任取一元素n,则所取两数m>n的概率是________.
8.集合A={(x,y)|y≥|x-1|},集合B={(x,y)|y≤-x+5}.先后掷两颗骰子,设掷第一颗骰子得点数记作a,掷第二颗骰子得点数记作b,则(a,b)∈A∩B的概率等于 .
9.(2010年江苏泰兴模拟)已知|x|≤2,|y|≤2,点P的坐标为(x,y),则当x,y∈Z时,P满足(x-2)2+(y-2)2≤4的概率为________.
10.(2010年皖南八校质检)甲、乙两人各掷一次骰子(均匀的正方体,六个面上分别为1,2,3,4,5,6点),所得点数分别为x,y.(1)求x0},在集合A中任取一个元素x ,则事件“x∈A∩B”的概率是________.
5.某公共汽车站每隔10分钟就有一趟车经过,小王随机赶到车站,则小王等车时间不超过4分钟的概率是________.
6.如图,M是半径为R的圆周上一个定点,在圆周上等可能地任取一点N,连结MN,则弦MN的长度超过R的概率是________.
7.已知Ω={(x,y)|x+y≤6,x≥0,y≥0},E={(x,y)|x-2y≥0,x≤4, y≥0},若向区域Ω内随机投一点P,则点P落入区域E的概率为________.
8.已知函数f(x)=-x2+ax-b.若a、b都是从区间[0,4]任取的一个数,则f(1)>0成立的概率是________.
9.在区间[0,1]上任意取两个实数a,b,则函数f(x)=x3+ax-b在区间[-1,1]上有且仅有一个零点的概率为________.
10.设不等式组表示的区域为A,不等式组表示的区域为B.
(1)在区域A中任取一点(x,y),求点(x,y)∈B的概率;
(2)若x,y分别表示甲、乙两人各掷一次骰子所得的点数,求点(x,y)在区域B中的概率.
11.(2010年江苏南通模拟)已知集合A={x|-1≤x≤0},集合B={x|ax+b·2x
-1<0,0≤a≤2,1≤b≤3}.(1)若a,b∈N,求A∩B≠∅的概率;
(2)若a,b∈R,求A∩B=∅的概率.
12.将长为1的棒任意地折成三段,求:三段的长度都不超过a(≤a≤1)的概率.
第十二章 导数
1、函数是定义在R上的可导函数,则是函数在时取得极值的__________条件
A、充分不必要 B、必要不充分 C、充要 D、既不充分也不必要
2、函数是定义在R上的可导函数,则为R上的单调增函数是的__________条件
A、充分不必要 B、必要不充分 C、充要 D、既不充分也不必要
3、已知上有最大值为3,那么此函数在[-2,2]上的最小值为
A、-37 B、-29 C、-5 D、-11
4、若函数
A、2 B、4 C、18 D、20
5、方程
A、0 B、1 C、2 D、3
6、若函数
7、函数
A、0 B、1 C、5 D、6
8、曲线
9、已知曲线上一点P处的切线与直线垂直,则此切线方程为
A、 B、 C、 D、
10、设点P是上的任一点,P点处的切线倾斜角为α,则角α的取值范围为
A、 B、 C、 D、
11、的图像如图(1)所示,则的图像最有可能的是
y
O
2
1
x
y
O
2
1
x
y
O
2
1
x
y
O
2
1
x
y
O
2
1
x
图(1) A B C D
12、已知等于
A、0 B、-4 C、-2 D、2
13、已知函数;
14、若函数的值为 ;
15、若直线的切线,则;
16、函数上是增函数,则实数 的取值范围为 ;
17、若函数;
18、已知曲线轴相切于不同于原点的一点,又函数有极小值为-4,求p、q的值。
19、设函数交于点P,若过P的切线方程为,且当x=2时,函数取极值-16,试求的解析式,并求这个函数的单调递减区间。
20、已知函数.(1)若函数在区间上递增,在区间上递减,求实数的值;(2)当时,设函数图像上任意一点处的切线的倾斜角为,若给定常数,+,求的取值范围。
第十三章 不等式
1、若为R上的减函数,且的充分不必要条件,则实数t的取值范围为 ( )
A、t≤0 B、t≥0 C、t≤-3 D、t≥-3
2、已知的取值范围为
A、 B(0,1) C、(0,1) D、(0,1)
3、已知奇函数
4、是定义在(0,3)上的函数,的图象如图所示,则不等式 的解集是
A.(0,1)(2,3)B.
C.(0,1) D.(0,1)(1,3)
5、函数在(-1,1)上有定义且的取值范围为
A、(-2,1) B、(0,) C、(0,1) D、(-2,)
6、已知函数,若,则的取值范围为
A、 B、 C、 D、
7、设奇函数在[-1,1]上是增函数,且,若函数对所有的都成立,当时t的取值范围为
A、[-2,2] B、 C、 D、
8、设点所在的区域的面积为
A、1 B、2 C、4 D、8
C(4,2)
B(5,1)
a(1,1)
y
x
O
9、在如图所示的坐标平面的可行域内(阴影部分且包括边界),
目标函数取得最优解有无数个,则的一个可能值为
A、-3 B、3 D、-1 D、1
10、若关于不等式的解集为 ;
11、若关于不等式的解集为 ;
12、若关于不等式的取值范围是 _______,若此不等式有解,则的取值范围是
13、为定义域为R的奇函数,不等式,则不等式的解集为 ;
14、已知关于的不等式取值范围为 ;
15、不等式对一切实数恒成立,则实数的取值范围为 ;
16、已知恒成立的实数的取值范围为 ;
17、关于的方程的两根分别在区间(0,1)与(1,2),则的取值范围为 ;
18、设的最小值为 ;
19、设的最大值为 ;
20、设
21、解关于的不等式
22.若a,b∈R,求证:≤+.
23. (2008·苏中三市调研)已知x、y、z均为正数.
求证:≥++.
第十四章 立体几何
第一节 简单几何体
A组
1.下列命题中,不正确的是______.
①棱长都相等的长方体是正方体
②有两个相邻侧面为矩形的棱柱为直棱柱
③有两个侧面与底面垂直的棱柱为直棱柱
④底面为平行四边形的四棱柱叫平行六面体
2.(2009年高考全国卷Ⅱ改编)纸制的正方体的六个面根据其方位分别标记为上、下、东、南、西、北,现在沿该正方体的一些棱将正方体剪开,外面朝上展平,得到如图的平面图形,则标“△”的面的方位是________.
3.(2009年高考安徽卷)对于四面体ABCD,下列命题正确的是________.
①相对棱AB与CD所在的直线是异面直线;
②由顶点A作四面体的高,其垂足是△BCD三条高线的交点;
③若分别作△ABC和△ABD的边AB上的高,则这两条高的垂足重合;
④任何三个面的面积之和都大于 第四个面的面积;
⑤分别作三组相对棱中点的连线,所得的三条线段相交于一点.
4.下列三个命题,其中正确的有________个.
①用一个平面去截棱锥,棱锥底面和截面之间的部分是棱台;
②两个底面平行且相似,其余各面都是梯形的多面体是棱台;
③有两个面互相平行,其余各面都是等腰梯形的六面体是棱台.
5.下面命题正确的有________个.
①长方形绕一条直线旋转一周所形成的几何体是圆柱
②过圆锥侧面上一点有无数条母线
③三棱锥的每个面都可以作为底面
④圆锥的轴截面(过轴所作的截面)是等腰三角形
6.如图所示,长方体的长、宽、高分别为4 cm,3 cm,5 cm,一只蚂蚁从A到C1点沿着表面爬行的最短距离是多少?
B组
1.(2009年高考安徽卷)对于四面体ABCD,下列命题正确的是________.
①相对棱AB与CD所在的直线是异面直线;
②由顶点A作四面体的高,其垂足是△BCD三条高线的交点;
③若分别作△ABC和△ABD的边AB上的高,则这两条高的垂足重合;
④任何三个面的面积之和都大于第四个面的面积;
⑤分别作三组相对棱中点的连线,所得的三条线段相交于一点.
2.下面是关于三棱锥的四个命题:
①底面是等边三角形,侧面与底面所成的二面角都相等的三棱锥是正三棱锥.
②底面是等边三角形,侧面都是等腰三角形的三棱锥是正三棱锥.
③底面是等边三角形,侧面的面积都相等的三棱锥是正三棱锥.
④侧棱与底面所成的角都相等,且侧面与底面所成的二面角都相等的三棱锥是正三棱锥.
其中,真命题的编号是______.(写出所有真命题的编号)
3.关于如图所示几何体的正确说法为________.
①这是一个六面体 ②这是一个四棱台
③这是一个四棱柱 ④这是一个四棱柱和三棱柱的组合体
⑤这是一个被截去一个三棱柱的四棱柱
4.(2009年高考安徽卷)对于四面体ABCD,下列命题正确的是________.
①相对棱AB与CD所在的直线是异面直线;
②由顶点A作四面体的高,其垂足是△BCD三条高线的交点;
③若分别作△ABC和△ABD的边AB上的高,则这两条高的垂足重合;
④任何三个面的面积之和都大于第四个面的面积;
⑤分别作三组相对棱中点的连线,所得的三条线段相交于一点.
5.给出以下命题:①底面是矩形的四棱柱是长方体;
②直角三角形绕着它的一边旋转一周形成的几何体叫做圆锥;
③四棱锥的四个侧面可以都是直角三角形.其中说法正确的是__________.
6.下列结论正确的是
①各个面都是三角形的几何体是三棱锥
②以三角形的一边所在直线为旋转轴,其余两边旋转形成的曲面所围成的几何体叫圆锥
③棱锥的侧棱长与底面多边形的边长相等,则该棱锥可能是正六棱锥
④圆锥的顶点与底面圆周上的任意一点的连线都是母线
7.过半径为2的球O表面上一点A作球O的截面,若OA与该截面所成的角是60°,则该截面的面积是________.
8.如果四棱锥的四条侧棱都相等,就称它为“等腰四棱锥”,四条侧棱称为它的腰,以下四个命题中,假命题是________.
①等腰四棱锥的腰与底面所成的角都相等
②等腰四棱锥的侧面与底面所成的二面角都相等或互补
③等腰四棱锥的底面四边形必存在外接圆
④等腰四棱锥的各顶点必在同一球面上
9.(2008年高考江西卷)如图(1),一个正四棱柱形的密闭容器水平放置,其底部镶嵌了同底的正四棱锥形实心装饰块,容器内盛有a升水时,水面恰好经过正四棱锥的顶点P.如果将容器倒置,水面也恰好过点P(图(2))
有下列四个命题:
A.正四棱锥的高等于正四棱柱高的一半
B.将容器侧面水平放置时,水面也恰好过点P
C.任意摆放该容器,当水面静止时,水面都恰好经过点P
D.若往容器内再注入a升水,则容器恰好能装满.
其中真命题的代号是:______(写出所有真命题的代号).
10.一个四棱锥和一个三棱锥恰好可以拼接成一个三棱柱,这个四棱锥的底面为正方形,且底面边长与各侧棱长相等,这个三棱锥的底面边长与各侧棱长也都相等.设四棱锥、三棱锥、三棱柱的高分别为h1,h2,h3,求h1∶h2∶h3的值.
11.一个等腰直角三角形的三个顶点分别在正三棱柱的三条侧棱上.已知正三棱柱的底面边长为2,求该三角形的斜边长.
12.(2009年高考辽宁卷改编)如果把地球看成一个球体,求地球上北纬60°纬线长和赤道线长的比值.
第二节 空间图形的基本关系与公理
A组
1.以下四个命题中,正确命题的个数是________.
①不共面的四点中,其中任意三点不共线;
②若点A、B、C、D共面,点A、B、C、E共面,则A、B、C、D、E共面;
③若直线a、b共面,直线a、c共面,则直线b、c共面;
④依次首尾相接的四条线段必共面.
2.给出下列四个命题:
①如果两个平面有三个公共点,那么这两个平面重合;
②两条直线可以确定一个平面;
③若M∈α,M∈β,α∩β=l,则M∈l;
④空间中,相交于同一点的三条直线在同一平面内.
其中真命题的个数为________.
3.(2009年高考湖南卷改编)平行六面体ABCD-A1B1C1D1中,既与AB共面也与CC1共面的棱的条数为________.
4.正方体ABCD-A1B1C1D1中,P、Q、R分别是AB、AD、B1C1的中点.那么,正方体的过P、Q、R的截面图形是________.
5.(原创题)已知直线m、n及平面α,其中m∥n,那么平面α内到两条直线m、n距离相等的点的集合可能是:(1)一条直线;(2)一个平面;(3)一个点;(4)空集.其中正确的是________.
6.如图,已知平面α、β,且α∩β=l.设梯形ABCD中,AD∥BC, 且AB⊂α,CD⊂β.求证:AB,CD,l共点(相交于一点).
B组
1.有以下三个命题:
①平面外的一条直线与这个平面最多有一个公共点;
②直线l在平面α内,可以用符号“l∈α”表示;
③若平面α内的一条直线a与平面β内的一条直线b相交,则α与β相交,
其中所有正确命题的序号是______________.
2.(2010年黄冈调研)下列命题中正确的是________.
①若△ABC在平面α 外,它的三条边所在的直线分别交α于P、Q、R,则P、Q、R三点共线;
②若三条直线a、b、c互相平行且分别交直线l于A、B、C三点,则这四条直线共面;
③空间中不共面的五个点一定能确定10个平面.
3.对于空间三条直线,有下列四个条件:
①三条直线两两相交且不共点
②三条直线两两平行
③三条直线共点
④有两条直线平行,第三条直线和这两条直线都相交
其中使三条直线共面的充分条件有:________.
4.(2008年高考浙江卷改编)对两条不相交的空间直线a与b,必存在平面α,使得________.
①a⊂α,b⊂α ②a⊂α,b∥α
③a⊥α,b⊥α ④a⊂α,b⊥α
5.正方体AC1中,E、F分别是线段C1D、BC的中点,则A1B与EF的位置关系是________.
6.(2010年湖南郴州调研)设α,β,γ是三个不重合的平面,l是直线,给出下列四个命题其中正确命题的序号是________.
①若α⊥β,l⊥β,则l∥α;
②若l⊥α,l∥β,则α⊥β;
③若l上有两点到α的距离相等,则l∥α;
④若α⊥β,α∥γ,则γ⊥β.
7.(2009年高考广东卷改编)给定下列四个命题:
①若一个平面内的两条直线与另一个平面都平行,那么这两个平面相互平行;
②若一个平面经过另一个平面的垂线,那么这两个平面相互垂直;
③垂直于同一直线的两条直线相互平行;
④若两个平面垂直,那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直.
其中,为真命题的是________.
8.(2009年高考宁夏、海南卷改编)如图所示,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E,F,且EF=,则下列结论中错误的是________.
①AC⊥BE
②EF∥平面ABCD
③三棱锥A-BEF的体积为定值
④异面直线AE,BF所成的角为定值
9.(2008年高考陕西卷改编)如图,α⊥β,α∩β=l,A∈α,B∈β,A、B到l的距离分别是a和b,AB与α、β所成的角分别是θ和φ,AB在α、β内的射影分别是m和n.若a>b,则θ与φ的大小关系为______,m与n的大小关系为______.
10.如图,已知正方体ABCD-A1B1C1D1中,E、F分别为D1C1、B1C1的中点,AC∩BD=P,A1C1∩EF=Q,若A1C交平面DBFE于R点,试确定R点的位置.
11.如图,在棱长为1的正方体ABCD-A1B1C1D1中,M为AB的中点,N为BB1的中点,O为平面BCC1B1的中心.
(1)过O作一直线与AN交于P,与CM交于Q
(2)求PQ的长.
12.(2008年高考四川卷)如图,平面ABEF⊥平面ABCD,四边形ABEF与ABCD都是直角梯形,∠BAD=∠FAB=90°,BC綊AD,BE綊FA,G、H分别为FA、FD的中点.
(1)证明:四边形BCHG是平行四边形;
(2)C、D、F、E四点是否共面?为什么?
(3)设AB=BE,证明:平面ADE⊥平面CDE.
第三节 平行关系
A组
1.已知m、n是两条不同直线,α,β是两个不同平面,下列命题中的真命题是________.
①如果m⊂α,n⊂β,m∥n,那么α∥β
②如果m⊂α,n⊂β,α∥β,那么m∥n
③如果m⊂α,n⊂β,α∥β且m,n共面,那么m∥n
④如果m∥n,m⊥α,n⊥β,那么α⊥β
2.已知m、n是不同的直线,α、β是不重合的平面,给出下列命题:
①若m∥α,则m平行于平面α内的无数条直线;
②若α∥β,m⊂α,n⊂β,则m∥n;
③若m⊥α,n⊥β,m∥n,则α∥β;
④若α∥β,m⊂α,则m∥β.
其中,真命题的序号是________.(写出所有真命题的序号)
3.(2010年苏北四市调研)给出下列关于互不相同的直线m、l、n和平面α、β的四个命题:
①若m⊂α,l∩α=A,点A∉m, 则l与m不共面;
②若m、l是异面直线,l∥α,m∥α,且n⊥l,n⊥m,则n⊥α;
③若l∥α,m∥β,α∥β,则l∥m;
④若l⊂α,m⊂α,l∩m=A,l∥β,m∥β,则α∥β.
其中为真命题的是________.
4.(2009年高考福建卷改编)设m,n是平面α内的两条不同直线;l1,l2是平面β内的两条相交直线,则α∥β的一个充分而不必要条件是________.
①m∥β且l1∥α ②m∥l1且n∥l2 ③m∥β且n∥β ④m∥β且n∥l2
5.(原创题)直线a∥平面α,α内有n条直线交于一点,则这n条直线中与直线a平行的直线有________条.
6.如图,ABCD为直角梯形,∠C=∠CDA=90°,AD=2BC=2CD,P为平面ABCD外一点,且PB⊥BD.
(1)求证:PA⊥BD;
(2)若PC与CD不垂直,求证:PA≠PD;
(3)若直线l过点P,且直线l∥直线BC,试在直线l上找一点E,使得直线PC∥平面EBD.
B组
1.已知m,n是两条不同的直线,α,β,γ是三个不同的平面,则下列命题正确的是________.
①若α⊥γ,α⊥β,则γ∥β ②若m∥n,m⊂α,n⊂β,则α∥β
③若m∥n,m∥α,则n∥α ④若n⊥α,n⊥β,则α∥β
2.已知m,n是两条不同的直线,α,β是两个不同的平面,有下列4个命题:
①若m∥n,n⊂α,则m∥α;
②若m⊥n,m⊥α,n⊄α,则n∥α;
③若α⊥β,m⊥α,n⊥β,则m⊥n;
④若m,n是异面直线,m⊂α,n⊂β,m∥β,则n∥α.
其中正确的命题有________.
3.已知m,n是平面α外的两条直线,且m∥n,则“m∥α”是“n∥α”的________条件.
4.设l1,l2是两条直线,α,β是两个平面,A为一点,下列命题中正确的命题是________.
①若l1⊂α,l2∩α=A,则l1与l2必为异面直线
②若α⊥β,l1⊂α,则l1⊥β
③l1⊂α,l2⊂β,l1∥β,l2∥α,则α∥β
④若l1∥α,l2∥l1,则l2∥α或l2⊂α
5.(2010年深圳模拟)若a不平行于平面α,且a⊄α,则下列结论成立的是________.
①α内的所有直线与a异面
②α内与a平行的直线不存在
③α内存在唯一的直线与a平行
④α内的直线与a都相交
6.设m、n是异面直线,则(1)一定存在平面α,使m⊂α且n∥α;(2)一定存在平面α,使m⊂α且n⊥α;(3)一定存在平面γ,使m、n到γ的距离相等;(4)一定存在无数对平面α与β,使m⊂α,n⊂β,且α∥β.上述4个命题中正确命题的序号为________.
7.如图,ABCD-A1B1C1D1是棱长为a的正方体,M、N分别是下底面的棱A1B1、B1C1的中点,P是上底面的棱AD上的一点,AP=,过P、M、N的平面交上底面于PQ,Q在CD上,则PQ=______.
8.下列四个正方体图形中,A、B为正方体的两个顶点,M、N、P分别为其所在棱的中点,能得出AB∥面MNP的图形的序号是________(写出所有符合要求的图形序号).
9.如图所示,在正方体ABCD-A1B1C1D1中,E、F、G、H分别是棱CC1、C1D1、D1D、CD的中点,N是BC中点.点M在四边形EFGH上及其内部运动,则M满足条件________时,有MN∥平面B1BDD1.
10.如图,长方体ABCD-A1B1C1D1中,AA1=,AB=1,AD=2,E为BC的中点,点M为棱AA1的中点.
(1)证明:DE⊥平面A1AE;
(2)证明:BM∥平面A1ED.
11.(2010年扬州调研)在正方体ABCD-A1B1C1D1中,M,N分别是AB,BC的中点.
(1)求证:平面B1MN⊥平面BB1D1D;
(2)若在棱DD1上有一点P,使BD1∥平面PMN,求线段DP与PD1的比
12.如图,四边形ABCD为矩形,BC⊥平面ABE,F为CE上的点,且BF⊥平面ACE.
(1)求证:AE⊥BE;
(2)设点M为线段AB的中点,点N为线段CE的中点.求证:MN∥平面DAE.
第四节 垂直关系
A组
1.设b、c表示两条直线,α,β表示两个平面,则下列命题是真命题的是________.
①若b⊂α,c∥α,则b∥c ②若b⊂α,b∥c,则c∥α
③若c∥α,α⊥β,则c⊥β ④若c∥α,c⊥β,则α⊥β
2.(2010年青岛质检)已知直线l⊥平面α,直线m⊂平面β,下面有三个命题:
①α∥β⇒l⊥m;②α⊥β⇒l∥m;③l∥m⇒α⊥β.则真命题的个数为________.
3.(2009年高考山东卷改编)已知α、β表示两个不同的平面,m为平面α内的一条直线,则“α⊥β ”是“m⊥β ”的________条件.
4.(2009年高考浙江卷)如图,在长方形ABCD中,AB=2,BC=1,E为DC的中点,F为线段EC(端点除外)上一动点.现将△AFD沿AF折起,使平面ABD⊥平面ABC.在平面ABD内过点D作DK⊥AB,K为垂足.设AK=t,则t的取值范围是________.
5.已知a、b为两条不同的直线,α、β为两个不同的平面,且a⊥α,b⊥β,则下列命题中假命题的有________.
①若a∥b,则α∥β; ②若α⊥β,则a⊥b;
③若a、b相交,则α、β相交; ④若α、β相交,则a,b相交.
6.(2009年高考山东卷)如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,AB=4,BC=CD=2,AA1=2,E,E1分别是棱AD,AA1的中点.
(1)设F是棱AB的中点,证明:直线EE1∥平面FCC1;
(2)证明:平面D1AC⊥平面BB1C1C.
B组
1.设a,b是两条不同的直线,α,β是两个不同的平面,则能得出a⊥b的是________.
①a⊥α,b∥β,α⊥β ②a⊥α,b⊥β,α∥β
③a⊂α,b⊥β,α∥β ④a⊂α,b∥β,α⊥β
2.设α,β为不重合的平面,m,n为不重合的直线,则下列命题正确的是________.
①若m⊂α,n⊂β,m∥n,则α∥β
②若n⊥α,n⊥β,m⊥β,则m⊥α
③若m∥α,n∥β,m⊥n,则α⊥β
④若α⊥β,α∩β=n,m⊥n,则m⊥α
3.设m,n是两条不同的直线, α,β是两个不同的平面,则下列命题正确的是________.
①m⊥α,n⊂β,m⊥n⇒α⊥β ②α∥β,m⊥α,n∥β ⇒m⊥n
③α⊥β,m⊥α,n∥β ⇒m⊥n ④α⊥β,α∩β=m,n⊥m⇒n⊥β
4.已知两条不同的直线m,n,两个不同的平面α,β,则下列命题中正确的是________.
①若m⊥α,n⊥β,α⊥β,则m⊥n
②若m⊥α,n∥β,α⊥β,则m⊥n
③若m∥α,n∥β,α∥β,则m∥n
④若m∥α,n⊥β,α⊥β,则m∥n
5.设a,b,c表示三条直线,α,β表示两个平面,则下列命题的逆命题不成立的是________.
①c⊥α,若c⊥β,则α∥β
②b⊂β,c是a在β内的射影,若b⊥c,则a⊥b
③b⊂β,若b⊥α,则β⊥α
④b⊂α,c⊄α,若c∥α,则b∥c
6.已知二面角α-l-β的大小为30°,m、n为异面直线,m⊥平面α,n⊥平面β,则m、n所成的角为________.
7.如图所示,在斜三棱柱ABC-A1B1C1中,∠BAC=90°,BC1⊥AC,则C1在底面ABC上的射影H必在直线______上.
8.(2010年江苏昆山模拟)在矩形ABCD中,AB=3,AD=4,P在AD上运动,设∠ABP=θ,将△ABP沿BP折起,使得平面ABP垂直于平面BPDC,AC长最小时θ的值为________.
9.在正四棱锥P-ABCD中,PA=AB,M是BC的中点,G是△PAD的重心,则在平面PAD中经过G点且与直线PM垂直的直线有________条.
10.如图,在三棱锥S-ABC中,OA=OB,O为BC中点,SO⊥平面ABC,E为SC中点,F为AB中点.
(1)求证:OE∥平面SAB;
(2)求证:平面SOF⊥平面SAB.
11.在长方体ABCD-A1B1C1D1中,AA1=2AB=2BC,E,F,E1分别是棱AA1,BB1,A1B1的中点.
(1)求证:CE∥平面C1E1F;
(2)求证:平面C1E1F⊥平面CEF.
12.(2010年江苏淮安模拟)如图,已知空间四边形ABCD中,BC=AC,AD=BD,E是AB的中点.
求证:(1)AB⊥平面CDE;
(2)平面CDE⊥平面ABC;
(3)若G为△ADC的重心,试在线段AE上确定一点F,使得GF∥平面CDE.
第五节 简单几何体的面积和体积
A组
1.(2010年东北四校联考)已知一个长方体的同一顶点处的三条棱长分别为1,,2,则其外接球的表面积为________.
2.(2009年高考上海卷)若等腰直角三角形的直角边长为2,则以一直角边所在的直线为轴旋转一周所成的几何体体积是_________.
3.(2010年南京调研)如图,在正三棱柱ABC-A1B1C1中,D为棱AA1的中点.若截面△BC1D
是面积为6的直角三角形,则此三棱柱的体积为________.
4.矩形ABCD中,AB=4,BC=3,沿AC将矩形ABCD折成一个直二面角
B-AC-D,则四面体ABCD的外接球的体积为________.
5.已知过球面上三点A、B、C的截面到球心的距离等于球半径的一半,且AC=BC=6,AB=4,则球的半径等于________,球的表面积等于________.
6.在长方体ABCD-A1B1C1D1中,AB=BC=2,过A1、C1、B三点的平面截去长方体的一个角后,得到如图所示的几何体ABCD-A1C1D1,且这个几何体的体积为.
(1)证明:直线A1B∥平面CDD1C1;
(2)求棱A1A的长;
(3)求经过A1,C1,B,D四点的球的表面积.
B组
1.(2008年高考湖北卷)用与球心距离为1的平面去截球,所得的截面面积为π,则球的体积为________.
2.在三棱锥A-BCD中,侧棱AB、AC、AD两两垂直,△ABC,△ACD,△ADB的面积分别为,,,则该三棱锥的体积为________.
3.(2010年福建厦门检测)已知一个球与一个正三棱柱的三个侧面和两个底面相切,若这个球的体积是,则这个三棱柱的体积是________.
4.(2009年高考陕西卷改编)若正方体的棱长为,则以该正方体各个面的中心为顶点的凸多面体的体积为________.
5.(2009年高考全国卷Ⅰ)已知OA为球O的半径,过OA的中点M且垂直于OA的平面截球面得到圆M.若圆M的面积为3π,则球O的表面积等于__________.
6.(2009年高考江西卷)体积为8的一个正方体,其全面积与球O的表面积相等,则球O的体积等于________.
7.若长方体的三个共顶点的面的面积分别是,,,则长方体的体积是________.
8.在一个锥体中,作平行于底面的截面,若这个截面面积与底面面积之比为1∶3,则锥体被截面所分成的两部分的体积之比为________
9.(2010年南通调研)正方体ABCD-A1B1C1D1的棱长为2,则四面体A-B1CD1的外接 球的体积为________.
10.(2009年高考宁夏、海南卷)如图,在三棱锥P-ABC中,△PAB是等边三角形,∠PAC=∠PBC=90°.
(1)证明:AB⊥PC;
(2)若PC=4,且平面PAC⊥平面PBC,求三棱锥
P-ABC的体积.
11.如图,已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB=2,F为CD的中点.
(1)求证:AF⊥平面CDE;
(2)求证:AF∥平面BCE;
(3)求四棱锥C-ABED的体积.
12.(2010年广州质检)如图,A1A是圆柱的母线,AB是圆柱底面圆的直径,C是底面圆周上异于A、B的任意一点,A1A=AB=2.
(1)求证:BC⊥平面A1AC;
(2)求三棱锥A1-ABC的体积的最大值.
第十五章 解析几何
第一节 直线的倾斜角、斜率及方程
A组
1.已知θ∈R,则直线xsinθ-y+1=0的倾斜角的取值范围是________.
2.已知直线l1的方程是ax-y+b=0,l2的方程是bx-y-a=0(ab≠0,a≠b),则下列各示意图形中,正确的是________.
3.直线mx-y+2m+1=0经过一定点,则该点的坐标是_______________.
4.(2008年高考浙江卷)已知a>0,若平面内三点A(1,-a),B(2,a2),C(3,a3)共线,则a=________.
5.(原创题)若点A(ab,a+b)在第一象限内,则直线bx+ay-ab=0不经过第________象限.
6.求过点P(2,3),且满足下列条件的直线方程:
(1)倾斜角等于直线x-3y+4=0的倾斜角的二倍的直线方程;
(2)在两坐标轴上截距相等的直线方程.
B组
1.直线l的倾角α满足4sinα=3cosα,而且它在x轴上的截距为3,则直线l的方程是__________.
2.已知直线y=kx-2k-1与直线x+2y-4=0的交点位于第一象限,则k的取值范围是________.
3.直线l与两直线y=1,x-y-7=0分别交于P、Q两点,线段PQ的中点恰为(1,-1),则直线l的斜率为________.
4.若直线(k2-1)x-y-1+2k=0不过第二象限,则实数k的取值范围是________.
5.(2010年苏州模拟)若ab<0,则过点P(0,-)与Q(,0)的直线PQ的倾斜角的取值范围是__________.
6.函数y=asinx-bcosx的一个对称轴方程为x=,则直线ax-by+c=0的倾斜角为______.
7.已知两直线a1x+b1y+1=0与a2x+b2y+1=0的交点是P(2,3),则过两点Q1(a1,b1),Q2(a2,b2)的直线方程是______________________.
8.直线ax+y+1=0与连结A(2,3),B(-3,2)的线段相交,则a的取值范围是__________.
9.(2010年湛江质检)已知在△ABC中,∠ACB=90°,BC=4,AC=3,P是AB上的一动点,则点P到AC,BC的距离乘积的最大值是________.
10.已知直线方程为(2+m)x+(1-2m)y+4-3m=0.
(1)证明:直线恒过定点M;
(2)若直线分别与x轴、y轴的负半轴交于A、B两点,求△AOB面积的最小值及此时直线的方程.
11.已知直线l:ay=(3a-1)x-1.
(1)求证:无论a为何值,直线l总过第三象限;
(2)a取何值时,直线l不过第二象限?
12.若直线l过点P(3,0)且与两条直线l1:2x-y-2=0,l2:x+y+3=0分别相交于两点A、B,且点P平分线段AB,求直线l的方程.
第二节 点与直线、直线与直线的位置关系
A组
1.(2009年高考安徽卷改编)直线l过点(-1,2)且与直线2x-3y+4=0垂直,则l的方程是________.
2.(2010年西安调研)已知两条直线y=ax-2和y=(a+2)x+1互相垂直,则a等于________.
3.(2010年苏州质检)直线x+ay+3=0与直线ax+4y+6=0平行的充要条件是a=________.
4.若点P(a,3)到直线4x-3y+1=0的距离为4,且点P在不等式2x+y-3<0表示的平面区域内,则实数a的值为________.
5.(原创题)在平面直角坐标系中,定义平面内与直线垂直的非零向量称为直线的法向量,若直线l过点A(-2,3),且法向量为n=(1,-2),则直线l的方程为________________.
6.直线y=2x是△ABC中∠C的角平分线所在的直线,若A、B的坐标分别为A(-4,2),B(3,1),求点C的坐标,并判断△ABC的形状.
B组
1.已知点P(3,2)与点Q(1,4)关于直线l对称,则直线l的方程为______________.
2.若三条直线l1:x+y=7,l2:3x-y=5,l3:2x+y+c=0不能围成三角形,则c的值为________.
3.已知两条直线l1:ax+by+c=0,直线l2:mx+ny+p=0,则an=bm是直线l1∥l2的________条件.
4.过点P(1,2)作直线l,使直线l与点M(2,3)和点N(4,-5)距离相等,则直线l的方程为________________.
5.已知直线l经过点(,2),其横截距与纵截距分别为a、b(a、b均为正数),则使a+b≥c恒成立的c的取值范围为________.
6.(2010年苏南四市调研)若函数y=ax+8与y=-x+b的图象关于直线y=x对称,则a+b=________.
7.如图,已知A(4,0)、B(0,4),从点P(2,0)射出的光线经直线AB反射后再射到直线OB上,最后经直线OB反射后又回到P点,则光线所经过的路程是______.
8.设a、b、c、分别是△ABC中∠A、∠B、∠C所对边的边长,则直线xsinA+ay+c=0与bx-ysinB+sinC=0的位置关系是______.
9.(2010年江苏常州模拟)已知00)与两坐标轴无公共点,那么实数k的取值范围为________.
2.若圆C的半径为1,圆心在第一象限,且与直线4x-3y=0和x轴都相切,则该圆的标准方程是________.
3.(2010年广东汕头调研)已知D是由不等式组,所确定的平面区域,则圆x2+y2=4在区域D内的弧长为________.
4.(2009年高考宁夏、海南卷改编)已知圆C1:(x+1)2+(y-1)2=1,圆C2与圆C1关于直线x-y-1=0对称,则圆C2的方程为________________.
5.(原创题)圆x2+y2-4x+2y+c=0与y轴交于A、B两点,其圆心为P,若∠APB=90°,则实数c的值是________.
6.已知点A(-3,0),B(3,0),动点P满足|PA|=2|PB|.
(1)若点P的轨迹为曲线C,求此曲线的方程;
(2)若点Q在直线l:x+y+3=0上,直线l2经过点Q且与曲线C只有一个公共点M,求|QM|的最小值,并求此时直线l2的方程.
B组
1.(2010年福州质检)圆心在直线2x-3y-1=0上的圆与x轴交于A(1,0),B(3,0)两点,则圆的方程为________________.
2.(2010年扬州调研)若直线ax+by=1过点A(b,a),则以坐标原点O为圆心,OA长为半径的圆的面积的最小值是___.
3.(2009年高考上海卷改编)点P(4,-2)与圆x2+y2=4上任一点连线的中点轨迹方程是____
4.已知点P(1,4)在圆C:x2+y2+2ax-4y+b=0上,点P关于直线x+y-3=0的对称点也在圆C上,则a=________,b=________.
5.已知圆的方程为x2+y2-6x-8y=0.设该圆过点(3,5)的最长弦和最短弦分别为AC和BD,则四边形ABCD的面积为___________.
6.过圆x2+y2=4外一点P(4,2)作圆的两条切线,切点为A、B,则△ABP的外接圆的方程是___________.
7.已知动点P(x,y)满足x2+y2-|x|-|y|=0,O为坐标原点,则PO的取值范围是______.
8.(2010年安徽合肥质检)曲线f(x)=xlnx在点P(1,0)处的切线l与坐标轴围成的三角形的外接圆方程是____________.
9.设实数x、y满足x2+(y-1)2=1,若对满足条件的x、y,不等式+c≥0恒成立,则c的取值范围是________.
10.如图,在平面直角坐标系xOy中,A(a,0)(a>0), B(0,a),C(-4,0),D(0,4),设△AOB的外接圆圆心为E.
(1)若⊙E与直线CD相切,求实数a的值;
(2)设点P在圆E上,使△PCD的面积等于12的点P有且只有三个,试问这样的⊙E是否存在,若存在?求出⊙E的标准方程;若不存在,说明理由.
11.在Rt△ABO中,∠BOA=90°,OA=8,OB=6,点P为它的内切圆C上任一点,求点P到顶点A、B、O距离的平方和的最大值和最小值.
12.(2008年高考江苏卷)在平面直角坐标系xOy中,设二次函数f(x)=x2+2x+b(x∈R)的图象与两个坐标轴有三个交点,经过这三个交点的圆记为C.
(1)求实数b的取值范围;
(2)求圆C的方程;
(3)问圆C是否经过某定点(其坐标与b无关)?请证明你的结论.
第四节 直线与圆、圆与圆的位置关系
A组
1.(2009年高考天津卷)若圆x2+y2=4与圆x2+y2+2ay-6=0(a>0)的公共弦的长为2,则a=________.
2.(2009年高考全国卷Ⅱ)已知圆O:x2+y2=5和点A(1,2),则过A且与圆O相切的直线与两坐标轴围成的三角形的面积等于________.
3.(2009年高考湖北卷)过原点O作圆x2+y2-6x-8y+20=0的两条切线,设切点分别为P、Q,则线段PQ的长为________.
4.若直线3x+4y+m=0与圆x2+y2-2x+4y+4=0没有公共点,则实数m的取值范围是________.
5.(原创题)已知直线x-y+2m=0与圆x2+y2=n2相切,其中m,n∈N*,且n-m<5,则满足条件的有序实数对(m,n)共有________个.
6.(2010年南京调研)已知:以点C(t,)(t∈R,t≠0)为圆心的圆与x轴交于点O、A,与y轴交于点O、B,其中O为原点.
(1)求证:△OAB的面积为定值;
(2)设直线y=-2x+4与圆C交于点M,N,若OM=ON,求圆C的方程.
B组
1.直线ax+by+b-a=0与圆x2+y2-x-3=0的位置关系是________.
2.(2010年秦州质检)已知直线y=-x与圆x2+y2=2相交于A、B两点,P是优弧AB上任意一点,则∠APB=____________.
3.已知向量a=(cosα,sinα),b=(cosβ,sinβ),a与b的夹角为60°,直线xcosα+ysinα=0与圆(x+cosβ)2+(y+sinβ)2=的位置关系是________.
4.过点A(11,2)作圆x2+y2+2x-4y-164=0的弦,其中弦长为整数的共有______条.
5.若集合A={(x,y)|y=1+},B={(x,y)|y=k(x-2)+4}.当集合A∩B有4个子集时,实数k的取值范围是________________.
6.(2009年高考全国卷Ⅱ)已知AC、BD为圆O:x2+y2=4的两条相互垂直的弦,垂足为M(1,),则四边形ABCD的面积的最大值为________.
7.(2010年宁波调研)已知圆C:x2+y2+bx+ay-3=0(a、b为正实数)上任意一点关于直线l:x+y+2=0的对称点都在圆C上,则+的最小值为________.
8.设圆O:x2+y2=,直线l:x+3y-8=0,点A∈l,使得圆O上存在点B,且∠OAB=30°(O为坐标原点),则点A的横坐标的取值范围是________.
9.(2009年高考江西卷)设直线系M:xcosθ+(y-2)sinθ=1(0≤θ≤2π),对于下列四个命题:
A.存在一个圆与所有直线相交
B.存在一个圆与所有直线不相交
C.存在一个圆与所有直线相切
D.M中的直线所能围成的正三角形面积都相等
其中真命题的代号是________(写出所有真命题的代号).
10.已知圆C1:x2+y2+2x+2y-8=0与圆C2:x2+y2-2x+10y-24=0相交于A、B两点,
(1)求公共弦AB所在的直线方程;
(2)求圆心在直线y=-x上,且经过A、B两点的圆的方程.
11.(2010年江苏徐州调研)已知圆C的方程为x2+y2=1,直线l1过定点A(3,0),且与圆C相切.
(1)求直线l1的方程;
(2)设圆C与x轴交于P、Q两点,M是圆C上异于P、Q的任意一点,过点A且与x轴垂直的直线为l2,直线PM交直线l2于点P′,直线QM交直线l2于点Q′.求证:以P′Q′为直径的圆C′总过定点,并求出定点坐标.
12.(2009年高考江苏卷)
如图在平面直角坐标系xOy中,已知圆C1:(x+3)2+(y-1)2=4和圆C2:(x-4)2+(y-5)2=4.
(1)若直线l过点A(4,0),且被圆C1截得的弦长为2,求直线l的方程;
(2)设P为平面上的点,满足:存在过点P的无穷多对互相垂直的直线l1和l2,它们分别与圆C1和C2相交,且直线l1被圆C1截得的弦长与直线l2被圆C2截得的弦长相等,试求所有满足条件的点P的坐标.
第五节 空间直角坐标系
A组
1.(2009年高考安徽卷)在空间直角坐标系中,已知点A(1,0,2),B(1,-3,1),点M在y轴上,且M到A与到B的距离相等,则M的坐标是________.
2.在空间直角坐标系中,以点A(4,1,9),B(10,-1,6),C(x,4,3)为顶点的△ABC是以BC为底边的等腰三角形,则实数x的值为________.
3.已知x、y、z满足方程C:(x-3)2+(y-4)2+(z+5)2=2,则x2+y2+z2的最小值是________.
4.(2010年广州调研)与A(3,4,5)、B(-2,3,0)两点距离相等的点M(x,y,z)满足的条件是________.
5.(原创题)已知A(3,5,-7)和点B(-2,4,3),点A在x轴上的射影为A′,点B在z轴上的射影为B′,则线段A′B′的长为________.
6.如图所示,正方体ABCD-A′B′C′D′的棱长为a,P、Q分别是D′B,B′C的中点,求PQ的长.
B组
1.已知△ABC的三个顶点坐标分别为A(2,3,1)、B(4,1,-2)、C(6,3,7),则△ABC的重心坐标为______.
2.设点B是点A(2,-3,5)关于xOy面的对称点,则|AB|等于______.
3.正方体不在同一表面上的两顶点A(-1,2,-1),B(3,-2,3),则正方体的体积为______.
4.(2010年江苏宜兴模拟)已知B是点A(3,7,-4)在xOy平面上的射影,则2等于______.
5.在z轴上与点A(-4,1,7)和点B(3,5,-2)等距离的点C的坐标为 ______.
6.在空间直线坐标系中,方程x2-4(y-1)2=0表示的图形是__________.
7.在空间直角坐标系中,正方体ABCD-A1B1C1D1的顶点A(3,-1,2),其中心M的坐标为(0,1,2),则该正方体的棱长为__________.
8.已知ABCD为平行四边形,且A(4,1,3)、B(2,-5,1),C(3,7,-5),则顶点D的坐标为________.
9.如图所示,在长方体OABC-O1A1B1C1中,OA=2,AB=3,AA1=2,M是OB1与BO1的交点,则M点的坐标是______.
10.如图所示,直三棱柱ABC-A1B1C1中,|C1C|=|CB|=|CA|=2,AC⊥CB,D、E分别是棱AB、B1C1的中点,F是AC的中点,求DE、EF的长度.
11.已知A(1,2,-1),B(2,0,2).
(1)在x轴上求一点P,使|PA|=|PB|;
(2)在xOz平面内的点M到A点与到B点等距离,求M点的轨迹.
12.在正四棱锥S-ABCD中,底面边长为a,侧棱长也为a,以底面中心O为坐标原点,建立如图所示的空间直角坐标系,P点在侧棱SC上,Q点在底面ABCD的对角线BD上,试求P、Q两点间的最小距离.
第十六章 圆锥曲线
1.椭圆(a>b>0)的两焦点为F1F2,连接点F1,F2为边作正三角形,若椭圆恰好平分正三角形的另两条边,则椭圆的离心率为
2.已知N(3,1),点A、B分别在直线y=x和y=0上,则△ABN的周长的最小值是 。
3.一个动圆的圆心在抛物线上,且动圆恒与直线相切,则此动圆必经过点______________
4.抛物线顶点在原点,焦点在y轴上,其上一点到焦点的距离为5,则此抛物线的方程为
5.椭圆的离心率为,那么双曲线的离心率为
6.已知椭圆的焦点是是椭圆上的一个动点,如果延长到,使得,那么动点的轨迹是 (写出曲线类型)
7.椭圆的焦点是,点P在椭圆上,如果线段的中点在y轴上,那么
8.过点且与抛物线仅有一个公共点的直线方程是
9.函数的图象为C,则C与x轴围成的封闭图形的面积为������____________.
10.若椭圆的左、右焦点分别为,抛物线的焦点为,若,则此椭圆的离心率为
11.已知双曲线的右顶点为A,而B、C是双曲线右支上两点,若三角形ABC为等边三角形,则m的取值范围是 。
12.长度为的线段AB的两个端点A、B都在抛物线上滑动,则线段AB的中点M到y轴的最短距离为 。
13.已知△ABC的顶点A(1,4),若点B在y轴上,点C在直线y=x上,则△ABC的周长的最小值是 。
14.设过点的直线l的斜率为k,若圆上恰有三点到直线l的距离等于1,则k的值是 。
15.设、是方程的两个不相等的实数根,那么过点和点 的直线与圆的位置关系是( )
A.相交 B.相切 C.相离 D.随的值变
化而变化
16.已知圆C过三点O(0,0),A(3,0),B(0,4),则与圆C相切且与坐标轴上截距相等的切线方程是 .
17.P是双曲线左支上一点,F1、F2分别是左、右焦点,且焦距为2c,则的内切圆的圆心横坐标为 .
18.在直角坐标平面上,O为原点,N为动点,||=6,.过点M作MM1⊥y轴于M1,过N作NN1⊥x轴于点N1,=+,记点T的轨迹为曲线C.
(Ⅰ)求曲线C的方程;
(Ⅱ)已知直线L与双曲线C1:5x2-y2=36的右支相交于P、Q两点(其中点P在第一象限),线段OP交轨迹C于A,若=3,SΔPAQ=-26tan∠PAQ,求直线L的方程.
19.设椭圆:的左、右焦点分别为,已知椭圆上的任意一点,满足,过作垂直于椭圆长轴的弦长为3.
(1)求椭圆的方程;
(2)若过的直线交椭圆于两点,求的取值范围.
20.已知双曲线的中心在坐标原点,焦点在x轴上,实轴长为2.一条斜率为的直线l过右焦点F与双曲线交于A,B两点,以AB为直径的圆与右准线交于M,N两点.
(1)若双曲线的离心率为,求圆的半径;
(2)设AB的中点为H,若,求双曲线的方程.