高考圆锥曲线题型之共线向量问题

高考圆锥曲线题型之共线向量问题

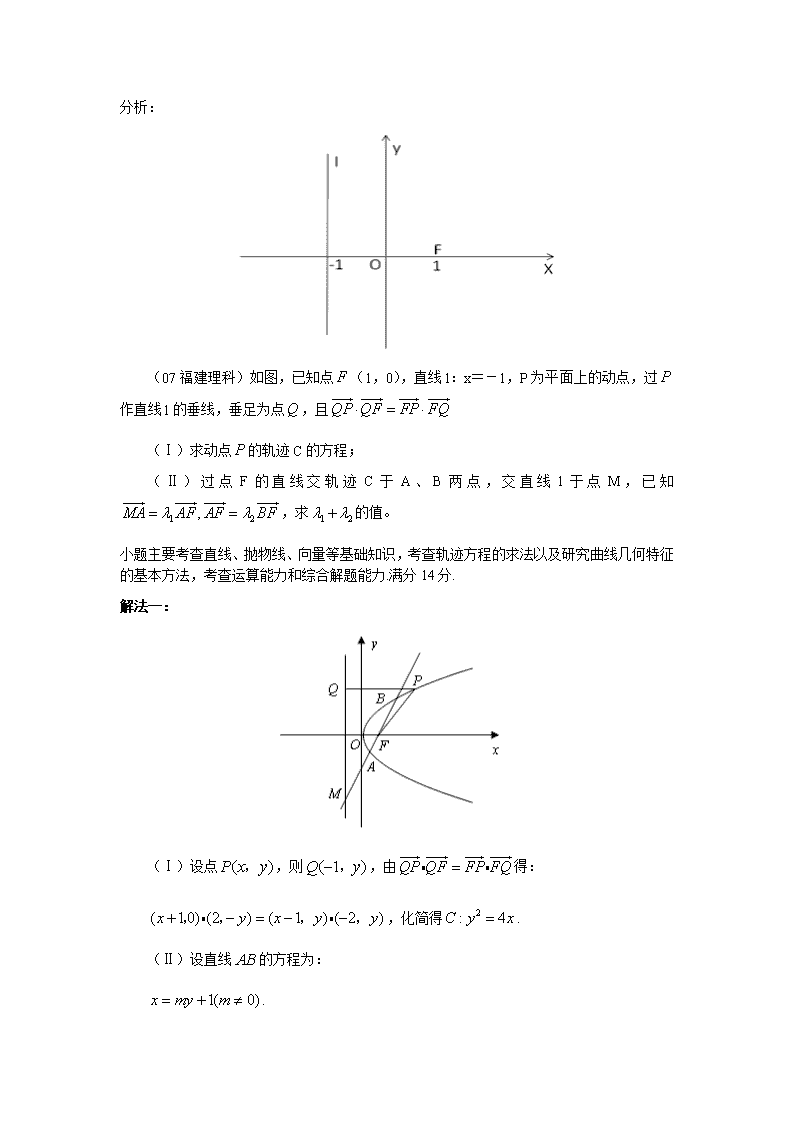
题型五：共线向量问题 解析几何中的向量共线，就是将向量问题转化为同类坐标的比例问题，再通过未达定理------同类坐标变换，将问题解决。此类问题不难解决。‎ 例题7、设过点D(0,3)的直线交曲线M：于P、Q两点，且,求实数的取值范围。‎ 分析：由可以得到，将P(x1,y1),Q(x2,y2),代人曲线方程，解出点的坐标，用表示出来。‎ 解：设P(x1,y1),Q(x2,y2), (x1,y1-3)=(x2,y2-3) 即 方法一：方程组消元法 又P、Q是椭圆+=1上的点 消去x2， 可得 即y2= 又－2y22， －22 解之得： 则实数的取值范围是。‎ 方法二：判别式法、韦达定理法、配凑法 设直线PQ的方程为：， 由消y整理后，得 ‎ ‎ P、Q是曲线M上的两点 ＝ 即 ① 由韦达定理得： ‎ ‎ 即 ② 由①得，代入②，整理得 ， 解之得 当直线PQ的斜率不存在，即时，易知或。 总之实数的取值范围是。 方法总结：通过比较本题的第二步的两种解法，可知第一种解法，比较简单，第二种方法是通性通法，但计算量较大，纵观高考中的解析几何题，若放在后两题，很多情况下能用通性通法解，但计算量较大，计算繁琐，考生必须有较强的意志力和极强的计算能力；不用通性通法，要求考生必须深入思考，有较强的思维能力，在命题人设计的框架中，找出破解的蛛丝马迹，通过自己的思维将问题解决。‎ 例题8：已知椭圆C的中心在原点，焦点在x轴上，它的一个顶点恰好是抛物线的焦点，离心率为．‎ ‎（1）求椭圆C的标准方程；‎ ‎（2）过椭圆C的右焦点F作直线l交椭圆C于A、B两点，交y轴于M点，若，，求的值．‎ 分析：‎ ‎（07福建理科）如图，已知点（1，0），直线l：x＝－1，P为平面上的动点，过作直线l的垂线，垂足为点，且 ‎（Ⅰ）求动点的轨迹C的方程；‎ ‎（Ⅱ）过点F的直线交轨迹C于A、B两点，交直线l于点M，已知，求的值。‎ 小题主要考查直线、抛物线、向量等基础知识，考查轨迹方程的求法以及研究曲线几何特征的基本方法，考查运算能力和综合解题能力.满分14分.‎ 解法一：‎ ‎（Ⅰ）设点，则，由得：‎ ‎，化简得.‎ ‎（Ⅱ）设直线的方程为： ‎ ‎.‎ 设，，又，‎ 联立方程组，消去得：‎ ‎，，故 由，得：‎ ‎，，整理得：‎ ‎，，‎ 解法二：‎ ‎（Ⅰ）由得：，‎ ‎，‎ ‎，‎ 所以点的轨迹是抛物线，由题意，轨迹的方程为：.‎ ‎（Ⅱ）由已知，，得.‎ 则：.…………①‎ 过点分别作准线的垂线，垂足分别为，，‎ 则有：.…………②‎ 由①②得：，即.‎ 练习：设椭圆的左、右焦点分别为、，A是椭圆C上的一点，且，坐标原点O到直线的距离为．‎ ‎（1）求椭圆C的方程；‎ ‎（2）设Q是椭圆C上的一点，过Q的直线l交x轴于点，较y轴于点M，若，求直线l的方程．‎ 山东2006理 双曲线C与椭圆有相同的焦点，直线y=为C的一条渐近线。‎ （I） 求双曲线C的方程；‎ ‎(II)过点P(0,4)的直线，交双曲线C于A,B两点，交x轴于Q点（Q点与C的顶点不重合）。当，且时，求Q点的坐标。‎ 解：‎ ‎（Ⅱ）解法一：‎ 由题意知直线的斜率存在且不等于零。‎ 设的方程：，‎ 则 在双曲线上，‎ 同理有：‎ 若则直线过顶点，不合题意.‎ 是二次方程的两根.‎ ‎，‎ 此时.‎ 所求的坐标为.‎ 解法二：‎ 由题意知直线的斜率存在且不等于零 设的方程，，则.‎ ‎，‎ 分的比为.‎ 由定比分点坐标公式得 下同解法一 解法三：‎ 由题意知直线的斜率存在且不等于零 设的方程：，则.‎ ‎，‎ ‎.‎ ‎，‎ ‎，，‎ 又，‎ 即 将代入得 ‎，否则与渐近线平行。‎ ‎。‎ 解法四：‎ 由题意知直线l得斜率k存在且不等于零，设的方程：，‎ 则 ‎,‎ ‎。‎ 同理 ‎ ‎.‎ 即 （*）‎ 又 ‎ 消去y得.‎ 当时，则直线l与双曲线得渐近线平行，不合题意，。‎ 由韦达定理有：‎ 代入（*）式得 ‎ 所求Q点的坐标为。‎ 练习：已知椭圆C的中心在原点，焦点在x轴上，它的一个顶点恰好是抛物线 的焦点，离心率等于。‎ ‎（1）求椭圆C的标准方程；‎ ‎（2）点P为椭圆上一点，弦PA、PB分别过焦点F1、F2，（PA、PB都不与x轴垂直，其点P的纵坐标不为0），若，求的值。‎ 解：（1）设椭圆C的方程为：，则b=1，由，得，则椭圆的方程为：‎ ‎（2）由得：，设，‎ 有得：‎ 解得：，‎ 根据PA、PB都不与x轴垂直，且，设直线PA的方程为：，代人，整理后，得：‎ 根据韦达定理，得：，则，‎ 从而，‎ 同理可求 则 由为椭圆上一点得：，‎ 则，‎ 故的值为18.‎