2009年山东省高考数学试卷(理科)【word版本、可编辑、附详细答案和解释】
2009年山东省高考数学试卷(理科)
一、选择题(共12小题,每小题5分,满分60分)
1. 集合A={0, 2, a},B={1, a2},若A∪B={0, 1, 2, 4, 16},则a的值为( )
A.0 B.1 C.2 D.4
2. i是虚数单位,3-i1-i=( )
A.1+2i B.1-2i C.2+i D.2-i
3. 将函数y=sin2x的图象向左平移π4个单位,再向上平移1个单位,所得图象的函数解析式是( )
A.y=2cos2x B.y=2sin2x
C.y=1+sin(2x+π4) D.y=cos2x
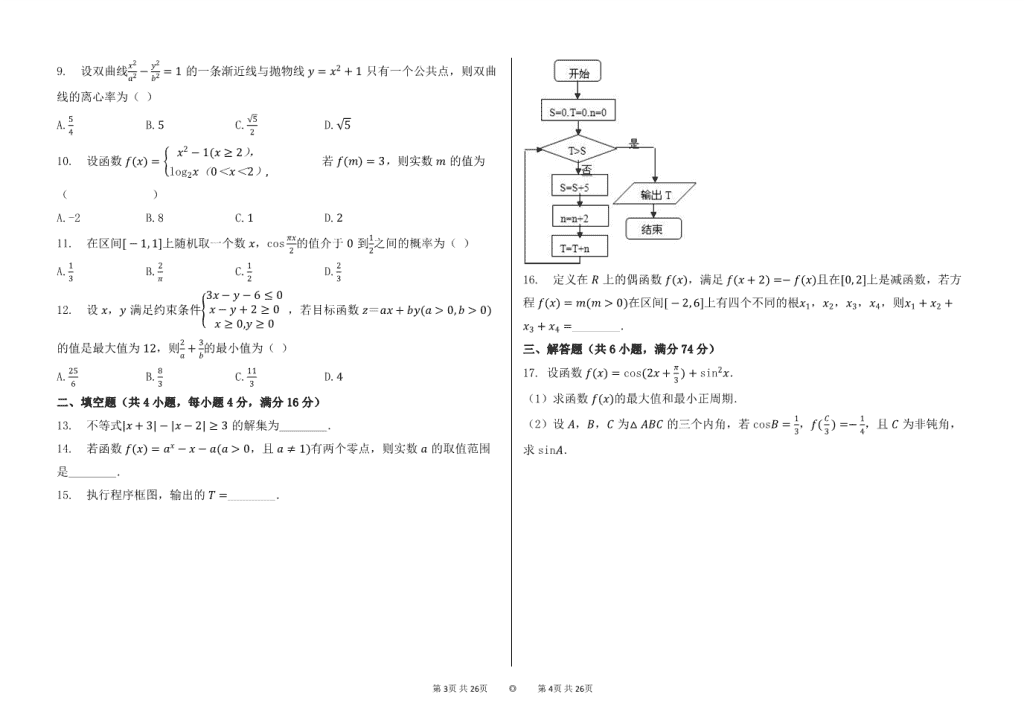
4. 一个空间几何体的三视图如图所示,则该几何体的体积为( )
A.2π+3π B.83π C.2π+33π D.4π+233π
5. 已知α,β表示两个不同的平面,m为平面α内的一条直线,则“α⊥β”是“m⊥β”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分又不必要条件
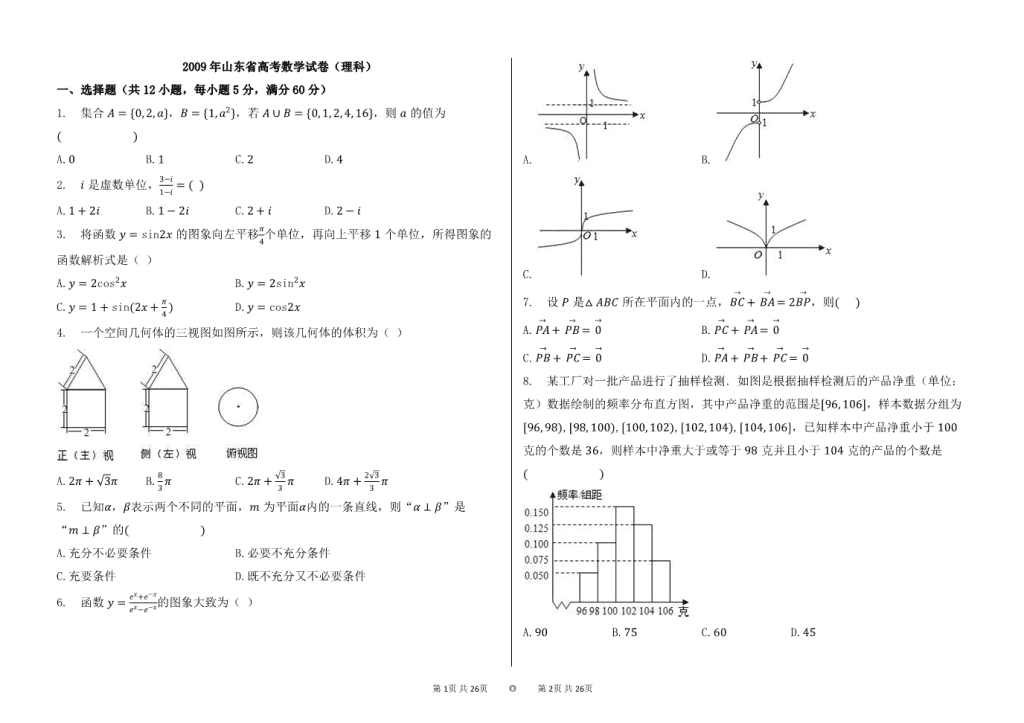
6. 函数y=ex+e-xex-e-x的图象大致为( )
A. B.
C. D.
7. 设P是△ABC所在平面内的一点,BC→+BA→=2BP→,则( )
A.PA→+PB→=0→ B.PC→+PA→=0→
C.PB→+PC→=0→ D.PA→+PB→+PC→=0→
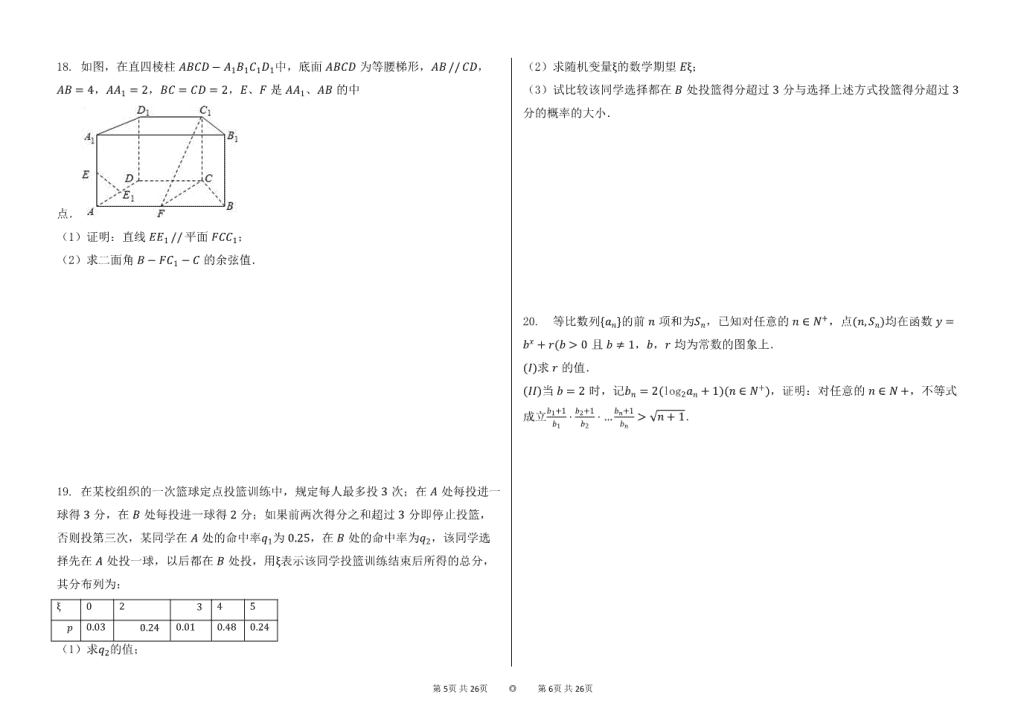
8. 某工厂对一批产品进行了抽样检测.如图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96, 106],样本数据分组为[96, 98),[98, 100),[100, 102),[102, 104),[104, 106],已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克并且小于104克的产品的个数是( )
A.90 B.75 C.60 D.45
第25页 共26页 ◎ 第26页 共26页
9. 设双曲线x2a2-y2b2=1的一条渐近线与抛物线y=x2+1只有一个公共点,则双曲线的离心率为( )
A.54 B.5 C.52 D.5
10. 设函数f(x)=x2-1(x≥2),log2x(0<x<2), 若f(m)=3,则实数m的值为( )
A.-2 B.8 C.1 D.2
11. 在区间[-1, 1]上随机取一个数x,cosπx2的值介于0到12之间的概率为( )
A.13 B.2π C.12 D.23
12. 设x,y满足约束条件3x-y-6≤0x-y+2≥0x≥0,y≥0 ,若目标函数z=ax+by(a>0, b>0)的值是最大值为12,则2a+3b的最小值为( )
A.256 B.83 C.113 D.4
二、填空题(共4小题,每小题4分,满分16分)
13. 不等式|x+3|-|x-2|≥3的解集为________.
14. 若函数f(x)=ax-x-a(a>0,且a≠1)有两个零点,则实数a的取值范围是________.
15. 执行程序框图,输出的T=________.
16. 定义在R上的偶函数f(x),满足f(x+2)=-f(x)且在[0, 2]上是减函数,若方程f(x)=m(m>0)在区间[-2, 6]上有四个不同的根x1,x2,x3,x4,则x1+x2+x3+x4=________.
三、解答题(共6小题,满分74分)
17. 设函数f(x)=cos(2x+π3)+sin2x.
(1)求函数f(x)的最大值和最小正周期.
(2)设A,B,C为△ABC的三个内角,若cosB=13,f(C3)=-14,且C为非钝角,求sinA.
第25页 共26页 ◎ 第26页 共26页
18. 如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰梯形,AB // CD,AB=4,AA1=2,BC=CD=2,E、F是AA1、AB的中点.
(1)证明:直线EE1 // 平面FCC1;
(2)求二面角B-FC1-C的余弦值.
19. 在某校组织的一次篮球定点投篮训练中,规定每人最多投3次;在A处每投进一球得3分,在B处每投进一球得2分;如果前两次得分之和超过3分即停止投篮,否则投第三次,某同学在A处的命中率q1为0.25,在B处的命中率为q2,该同学选择先在A处投一球,以后都在B处投,用ξ表示该同学投篮训练结束后所得的总分,其分布列为:
ξ
0
2
3
4
5
p
0.03
0.24
0.01
0.48
0.24
(1)求q2的值;
(2)求随机变量ξ的数学期望Eξ;
(3)试比较该同学选择都在B处投篮得分超过3分与选择上述方式投篮得分超过3分的概率的大小.
20. 等比数列{an}的前n项和为Sn,已知对任意的n∈N+,点(n, Sn)均在函数y=bx+r(b>0且b≠1,b,r均为常数的图象上.
(I)求r的值.
(II)当b=2时,记bn=2(log2an+1)(n∈N+),证明:对任意的n∈N+,不等式成立b1+1b1⋅b2+1b2⋅…bn+1bn>n+1.
第25页 共26页 ◎ 第26页 共26页
21. 两城市A和B相距20km,现计划在两城市外以AB为直径的半圆弧AB上选择一点C建造垃圾处理厂,其对城市的影响度与所选地点到城市的距离有关,对城A和城B的总影响度为城A与城B的影响度之和,记C点到城A的距离为x km,建在C处的垃圾处理厂对城A和城B的总影响度为y,统计调查表明:垃圾处理厂对城A的影响度与所选地点到城A的距离的平方成反比,比例系数为4;对城B的影响度与所选地点到城B的距离的平方成反比,比例系数为k,当垃圾处理厂建在AB的中点时,对城A和城B的总影响度为0.065.
(1)将y表示成x的函数;
(2)判断弧AB上是否存在一点,使建在此处的垃圾处理厂对城A和城B的总影响度最小?若存在,求出该点到城A的距离;若不存在,说明理由.
22. 设椭圆E:x2a2+y2b2=1(a, b>0)M(2, 2),N(6, 1),O为坐标原点
(I)求椭圆E的方程;
(II)是否存在圆心在原点的圆,使得该圆的任意一条切线与椭圆E恒在两个交点A,B且OA→⊥OB→?若存在,写出该圆的方程,关求|AB|的取值范围;若不存在,说明理由.
第25页 共26页 ◎ 第26页 共26页
参考答案与试题解析
2009年山东省高考数学试卷(理科)
一、选择题(共12小题,每小题5分,满分60分)
1.D
【分析】
解:∵ A={0, 2, a},B={1, a2},A∪B={0, 1, 2, 4, 16},
∴ a2=16,a=4,
∴ a=4,
故选D.
2.C
【分析】
解:3-i1-i=(3-i)(1+i)(1-i)(1+i)=4+2i2=2+i
故选C.
3.A
【分析】
解:将函数y=sin2x的图象向左平移π4个单位,
得到函数y=sin2(x+π4)=cos2x的图象,
再向上平移1个单位,所得图象的函数解析式为y=1+cos2x=2cos2x,
故选A.
4.C
【分析】
解:所求几何体为一个圆柱体和圆锥体构成.
其中圆锥的高为22-12=3.其体积为13π⋅12⋅3=33π
圆柱的体积为π⋅12⋅2=2π
故此简单组合体的体积V=33π+2π
故选C.
5.B
【分析】
解:由平面与平面垂直的判定定理知,
如果m为平面α内的一条直线,
且m⊥β,则α⊥β,
反之,α⊥β时,若m平行于α和β的交线,则m // β,
所以不一定能得到m⊥β,
所以“α⊥β”是“m⊥β”的必要不充分条件.
故选B.
6.A
【分析】
解析:函数有意义,需使ex-e-x≠0,
其定义域为{x|x≠0},排除C,D,
又因为y=ex+e-xex-e-x=e2x+1e2x-1=1+2e2x-1,
所以当x>0时函数为减函数,故选A
故选:A.
7.B
【分析】
解:∵ BC→+BA→=2BP→,
∴ BC→-BP→=BP→-BA→,
∴ PC→=AP→,
∴ PC→-AP→=0→,
第25页 共26页 ◎ 第26页 共26页
∴ PC→+PA→=0→.
故选B.
8.A
【分析】
解:净重大于或等于98克并且小于104克的产品的个数设为N2,
产品净重小于100克的个数设为N1=36,样本容量为N,
则N2N1=(0.1+0.15+0.125)×2×N(0.05+0.1)×2×N=375150,
N2=375150×36=90.
故选A.
9.D
【分析】
解:双曲线x2a2-y2b2=1的一条渐近线为y=bax,
由方程组y=baxy=x2+1,消去y,
x2-bax+1=0有唯一解,
所以△=(ba)2-4=0,
所以ba=2,e=ca=a2+b2a=1+(ba)2=5,
故选D
10.C
【分析】
解:将m代入分段函数当中,当m2-1=3时,m=2,-2.
∵ x≥2,所以m=-2舍去.
当log2x=3时,x=8.∵ 0<x<2,∴ x=8舍去,
故m=2.
故选D.
11.A
【分析】
在区间[-1, 1]上随机取一个数x,
即x∈[-1, 1]时,要使cosπx2的值介于0到12之间,
需使-π2≤πx2≤-π3或π3≤πx2≤π2
∴ -1≤x≤-23或23≤x≤1,区间长度为23,
由几何概型知cosπx2的值介于0到12之间的概率为232=13.
12.A
【分析】
不等式表示的平面区域如图所示阴影部分,
当直线ax+by=z(a>0, b>0)
过直线x-y+2=0与直线3x-y-6=0的交点(4, 6)时,
目标函数z=ax+by(a>0, b>0)取得最大12,
即4a+6b=12,即2a+3b=6,而2a+3b=(2a+3b)2a+3b6=136+(ba+ab)≥136+2=256,
二、填空题(共4小题,每小题4分,满分16分)
13.{x|x≥1}
【分析】
解:当x<-3时,因为原不等式|x+3|-|x-2|≥3去绝对值号得:-(x+3)+(x-2)≥3可推出-5≥3,这显然不可能,
当-3≤x≤2时,因为原不等式|x+3|-|x-2|≥3去绝对值号得:(x+3)+(x-2)≥3可推出,x≥1,故当1≤x≤2不等式成立.
当x>2时,因为原不等式|x+3|-|x-2|≥3去绝对值号得:(x+3)-(x-2)≥3可推出5≥3,这显然恒成立.
故综上所述,不等式的解集为x|x≥1,
第25页 共26页 ◎ 第26页 共26页
故答案为{x|x≥1}.
14.(1, +∞)
【分析】
解:令g(x)=ax(a>0,且a≠1),h(x)=x+a,有0
1两种情况.如图所示:
在同一坐标系中画出两个函数的图象,若函数f(x)=ax-x-a有两个不同的零点,则函数g(x),h(x)的图象有两个不同的交点.根据画出的图象只有当a>1时符合题目要求.
故答案为:(1, +∞).
15.30
【分析】
解:按照程序框图依次执行为S=5,n=2,T=2;
S=10,n=4,T=2+4=6;S=15,n=6,T=6+6=12;
S=20,n=8,T=12+8=20;S=25,n=10,T=20+10=30>S,输出T=30.
故答案为:30.
16.8
【分析】
解:∵ f(x+2)=-f(x)
∴ f(x)=-f(x-2)
∴ f(x-2)=f(x+2)
即 f(x)=f(x+4)
∴ f(x)是一个周期函数,周期为4
又函数是偶函数,所以f(x)关于y轴对称.
由f(x)在[0, 2]上是减函数,可做函数图象示意图如图
设x1=|n→||n1|→˙=22×7=77,
由图可知二面角B-FC1-C为锐角,所以二面角B-FC1-C的余弦值为77.
【分析】
(1)证明:因为AB=4,BC=CD=2,F是棱AB的中点,
所以BF=BC=CF,△BCF为正三角形,
因为ABCD为等腰梯形,所以∠BAD=∠ABC=60∘,
取AF的中点M,并连接DM,则DM⊥AB,所以DM⊥CD,
以DM为x轴,DC为y轴,DD1为z轴建立空间直角坐标系,
则D(0, 0, 0),A(3, -1, 0),F(3, 1, 0),C(0, 2, 0),
第25页 共26页 ◎ 第26页 共26页
C1(0, 2, 2),E(32, -12, 0),E1(3, -1, 1),
所以EE1→=(32,-12,1),
CF→=(3,-1,0),CC1→=(0,0,2),FC1→=(-3,1,2)
设平面CC1F的法向量为n→=(x,y,z)
则n→⋅CC1→=0˙所以3x-y=0z=0
取n→=(1,3,0),
则n→⋅EE1→=32×1-12×3+1×0=0,
所以n→⊥EE1→,所以直线EE1 // 平面FCC1.
(2)解:FB→=(0,2,0),
设平面BFC1的法向量为n1→=(x1,y1,z1),
则n1→⋅FC1→=0˙所以y1=0-3x1+y1+2z1=0,
取n1→=(2,0,3),
则n→⋅n1→=2×1-3×0+0×3=2,|n→|=1+(3)2=2,
|n1→|=22+0+(3)2=7,
所以cos⟨n→,n1→>=|n→||n1|→˙=22×7=77,
由图可知二面角B-FC1-C为锐角,所以二面角B-FC1-C的余弦值为77.
19.解:(1)设该同学在A处投中为事件A,
在B处投中为事件B,则事件A,B相互独立,
且P(A)=0.25,P(A¯)=0.75,P(B)=q2,P(B¯)=1-q2.
根据分布列知:ξ=0时P(A¯B¯B¯)=P(A¯)P(B¯)P(B¯)=0.75(1-q2)2=0.03,
所以1-q2=0.2,q2=0.8;
(2)当ξ=2时,P1=P=(A¯BB¯+A¯B¯B)=P(A¯BB¯)+P(A¯B¯B)
=P(A¯)P(B)P(B¯)+P(A¯)P(B¯)P(B)
=0.75q2(1-q2)×2=1.5q2(1-q2)=0.24
当ξ=3时,P2=P(AB¯B¯)=P(A)P(B¯)P(B¯)=0.25(1-q2)2=0.01,
当ξ=4时,P3=P(A¯BB)P(A¯)P(B)P(B)=0.75q22=0.48,
当ξ=5时,P4=P(AB¯B+AB)=P(AB¯B)+P(AB)
=P(A)P(B¯)P(B)+P(A)P(B)=0.25q2(1-q2)+0.25q2=0.24
随机变量ξ的数学期望Eξ=0×0.03+2×0.24+3×0.01+4×0.48+5×0.24=3.63;
(3)该同学选择都在B处投篮得分超过的概率为P(B¯BB+BB¯B+BB)
=P(B¯BB)+P(BB¯B)+P(BB)=2(1-q2)q22+q22=0.896;
该同学选择(1)中方式投篮得分超过3分的概率为0.48+0.24=0.72.
由此看来该同学选择都在B处投篮得分超过3分的概率大.
【分析】
解:(1)设该同学在A处投中为事件A,
第25页 共26页 ◎ 第26页 共26页
在B处投中为事件B,则事件A,B相互独立,
且P(A)=0.25,P(A¯)=0.75,P(B)=q2,P(B¯)=1-q2.
根据分布列知:ξ=0时P(A¯B¯B¯)=P(A¯)P(B¯)P(B¯)=0.75(1-q2)2=0.03,
所以1-q2=0.2,q2=0.8;
(2)当ξ=2时,P1=P=(A¯BB¯+A¯B¯B)=P(A¯BB¯)+P(A¯B¯B)
=P(A¯)P(B)P(B¯)+P(A¯)P(B¯)P(B)
=0.75q2(1-q2)×2=1.5q2(1-q2)=0.24
当ξ=3时,P2=P(AB¯B¯)=P(A)P(B¯)P(B¯)=0.25(1-q2)2=0.01,
当ξ=4时,P3=P(A¯BB)P(A¯)P(B)P(B)=0.75q22=0.48,
当ξ=5时,P4=P(AB¯B+AB)=P(AB¯B)+P(AB)
=P(A)P(B¯)P(B)+P(A)P(B)=0.25q2(1-q2)+0.25q2=0.24
随机变量ξ的数学期望Eξ=0×0.03+2×0.24+3×0.01+4×0.48+5×0.24=3.63;
(3)该同学选择都在B处投篮得分超过的概率为P(B¯BB+BB¯B+BB)
=P(B¯BB)+P(BB¯B)+P(BB)=2(1-q2)q22+q22=0.896;
该同学选择(1)中方式投篮得分超过3分的概率为0.48+0.24=0.72.
由此看来该同学选择都在B处投篮得分超过3分的概率大.
20.解:(1)因为对任意的n∈N+,点(n, Sn),
均在函数y=bx+r(b>0且b≠1,b,r均为常数的图象上.
所以得Sn=bn+r,当n=1时,a1=S1=b+r,
当n≥2时,an=Sn-Sn-1=bn+r-(bn-1+r)=bn-bn-1=(b-1)bn-1,
又因为{an}为等比数列,所以r=-1,公比为b,an=(b-1)bn-1
(2)当b=2时,an=(b-1)bn-1=2n-1,bn=2(log2an+1)=2(log22n-1+1)=2n
则bn+1bn=2n+12n,
所以b1+1b1⋅b2+1b2…bn+1bn=32⋅54⋅76…2n+12n
下面用数学归纳法证明不等式b1+1b1⋅b2+1b2…bn+1bn=32⋅54⋅76…2n+12n>n+1成立.
当n=1时,左边=32,右边=2,
因为32>2,所以不等式成立.
假设当n=k时不等式成立,
即b1+1b1⋅b2+1b2…bn+1bn=32⋅54⋅76…2k+12k>k+1成立
则当n=k+1时,
左边=b1+1b1⋅b2+1b2…bk+1bk⋅bk+1+1bk+1=32⋅54⋅76…2k+12k⋅2k+32k+2>k+1⋅2k+32k+2=(2k+3)24(k+1)=4(k+1)2+4(k+1)+14(k+1)=(k+1)+1+14(k+1)>(k+1)+1
所以当n=k+1时,不等式也成立.
由①、②可得不等式恒成立.
【分析】
解:(1)因为对任意的n∈N+,点(n, Sn),
均在函数y=bx+r(b>0且b≠1,b,r均为常数的图象上.
所以得Sn=bn+r,当n=1时,a1=S1=b+r,
当n≥2时,an=Sn-Sn-1=bn+r-(bn-1+r)=bn-bn-1=(b-1)bn-1,
又因为{an}为等比数列,所以r=-1,公比为b,an=(b-1)bn-1
(2)当b=2时,an=(b-1)bn-1=2n-1,bn=2(log2an+1)=2(log22n-1+1)=2n
则bn+1bn=2n+12n,
所以b1+1b1⋅b2+1b2…bn+1bn=32⋅54⋅76…2n+12n
下面用数学归纳法证明不等式b1+1b1⋅b2+1b2…bn+1bn=32⋅54⋅76…2n+12n>n+1成立.
第25页 共26页 ◎ 第26页 共26页
当n=1时,左边=32,右边=2,
因为32>2,所以不等式成立.
假设当n=k时不等式成立,
即b1+1b1⋅b2+1b2…bn+1bn=32⋅54⋅76…2k+12k>k+1成立
则当n=k+1时,
左边=b1+1b1⋅b2+1b2…bk+1bk⋅bk+1+1bk+1=32⋅54⋅76…2k+12k⋅2k+32k+2>k+1⋅2k+32k+2=(2k+3)24(k+1)=4(k+1)2+4(k+1)+14(k+1)=(k+1)+1+14(k+1)>(k+1)+1
所以当n=k+1时,不等式也成立.
由①、②可得不等式恒成立.
21.解:(1)由题意得y=4x2+k400-x2,
又∵ 当x=102时,y=0.065,
∴ k=9
∴ y=4x2+9400-x2(x∈(0,20))
(2)y=4x2+9400-x2=5(x2+320)-x4+400x2,
令t=x2+320∈(320, 720),
则y=5-(t+230400t)+1040≥116,当且仅当t=480即x=410时,等号成立.
∴ 弧AB上存在一点,该点到城A的距离为410时,使建在此处的垃圾处理厂对城A和城B的总影响度最小为0.0625.
【分析】
解:(1)由题意得y=4x2+k400-x2,
又∵ 当x=102时,y=0.065,
∴ k=9
∴ y=4x2+9400-x2(x∈(0,20))
(2)y=4x2+9400-x2=5(x2+320)-x4+400x2,
令t=x2+320∈(320, 720),
则y=5-(t+230400t)+1040≥116,当且仅当t=480即x=410时,等号成立.
∴ 弧AB上存在一点,该点到城A的距离为410时,使建在此处的垃圾处理厂对城A和城B的总影响度最小为0.0625.
22.解:(1)因为椭圆E:x2a2+y2b2=1(a, b>0)
过M(2, 2),N(6, 1)两点,
所以4a2+2b2=16a2+1b2=1解得1a2=181b2=14
所以a2=8b2=4椭圆E的方程为x28+y24=1
(2)假设存在圆心在原点的圆,
使得该圆的任意一条切线与椭圆E恒有两个交点A,B,
且OA→⊥OB→,设该圆的切线方程为y=kx+m解方程组y=kx+mx28+y24=1
得x2+2(kx+m)2=8,即(1+2k2)x2+4kmx+2m2-8=0,
则△=16k2m2-4(1+2k2)(2m2-8)=8(8k2-m2+4)>0,
即8k2-m2+4>0x1+x2=-4km1+2k2x1x2=2m2-81+2k2,y1y2=(kx1+m)(kx2+m)=k2x1x2+km(x1+x2)+m2=k2(2m2-8)1+2k2-4k2m21+2k2+m2=m2-8k21+2k2
要使OA→⊥OB→,
需使x1x2+y1y2=0,
第25页 共26页 ◎ 第26页 共26页
即2m2-81+2k2+m2-8k21+2k2=0,
所以3m2-8k2-8=0,所以k2=3m2-88≥0又8k2-m2+4>0,
所以m2>23m2≥8,所以m2≥83,
即m≥263或m≤-263,
因为直线y=kx+m为圆心在原点的圆的一条切线,
所以圆的半径为r=|m|1+k2,
r2=m21+k2=m21+3m2-88=83,
r=263,所求的圆为x2+y2=83,
此时圆的切线y=kx+m都满足m≥263或m≤-263,
而当切线的斜率不存在时切线为x=±263与椭圆x28+y24=1的两个交点为(263,±263)或(-263,±263)满足OA→⊥OB→,综上,
存在圆心在原点的圆x2+y2=83,
使得该圆的任意一条切线与椭圆E恒有两个交点A,B,且OA→⊥OB→.
因为x1+x2=-4km1+2k2x1x2=2m2-81+2k2,
所以(x1-x2)2=(x1+x2)2-4x1x2=(-4km1+2k2)2-4×2m2-81+2k2=8(8k2-m2+4)(1+2k2)2,|AB|=(x1-x2)2+(y1-y2)2=(1+k2)(x1-x2)2=(1+k2)8(8k2-m2+4)(1+2k2)2=323⋅4k4+5k2+14k4+4k2+1=323[1+k24k4+4k2+1],
①当k≠0时|AB|=323[1+14k2+1k2+4]
因为4k2+1k2+4≥8所以0<14k2+1k2+4≤18,
所以323<323[1+14k2+1k2+4]≤12,
所以436<|AB|≤23当且仅当k=±22时取”=”.
2当k=0时,|AB|=463
【分析】
解:(1)因为椭圆E:x2a2+y2b2=1(a, b>0)
过M(2, 2),N(6, 1)两点,
所以4a2+2b2=16a2+1b2=1解得1a2=181b2=14
所以a2=8b2=4椭圆E的方程为x28+y24=1
(2)假设存在圆心在原点的圆,
使得该圆的任意一条切线与椭圆E恒有两个交点A,B,
且OA→⊥OB→,设该圆的切线方程为y=kx+m解方程组y=kx+mx28+y24=1
得x2+2(kx+m)2=8,即(1+2k2)x2+4kmx+2m2-8=0,
则△=16k2m2-4(1+2k2)(2m2-8)=8(8k2-m2+4)>0,
即8k2-m2+4>0x1+x2=-4km1+2k2x1x2=2m2-81+2k2,y1y2=(kx1+m)(kx2+m)=k2x1x2+km(x1+x2)+m2=k2(2m2-8)1+2k2-4k2m21+2k2+m2=m2-8k21+2k2
要使OA→⊥OB→,
需使x1x2+y1y2=0,
第25页 共26页 ◎ 第26页 共26页
即2m2-81+2k2+m2-8k21+2k2=0,
所以3m2-8k2-8=0,所以k2=3m2-88≥0又8k2-m2+4>0,
所以m2>23m2≥8,所以m2≥83,
即m≥263或m≤-263,
因为直线y=kx+m为圆心在原点的圆的一条切线,
所以圆的半径为r=|m|1+k2,
r2=m21+k2=m21+3m2-88=83,
r=263,所求的圆为x2+y2=83,
此时圆的切线y=kx+m都满足m≥263或m≤-263,
而当切线的斜率不存在时切线为x=±263与椭圆x28+y24=1的两个交点为(263,±263)或(-263,±263)满足OA→⊥OB→,综上,
存在圆心在原点的圆x2+y2=83,
使得该圆的任意一条切线与椭圆E恒有两个交点A,B,且OA→⊥OB→.
因为x1+x2=-4km1+2k2x1x2=2m2-81+2k2,
所以(x1-x2)2=(x1+x2)2-4x1x2=(-4km1+2k2)2-4×2m2-81+2k2=8(8k2-m2+4)(1+2k2)2,|AB|=(x1-x2)2+(y1-y2)2=(1+k2)(x1-x2)2=(1+k2)8(8k2-m2+4)(1+2k2)2=323⋅4k4+5k2+14k4+4k2+1=323[1+k24k4+4k2+1],
①当k≠0时|AB|=323[1+14k2+1k2+4]
因为4k2+1k2+4≥8所以0<14k2+1k2+4≤18,
所以323<323[1+14k2+1k2+4]≤12,
所以436<|AB|≤23当且仅当k=±22时取”=”.
2当k=0时,|AB|=463
第25页 共26页 ◎ 第26页 共26页