- 2021-04-12 发布 |
- 37.5 KB |
- 38页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2020_2021学年新教材高中数学第五章三角函数5
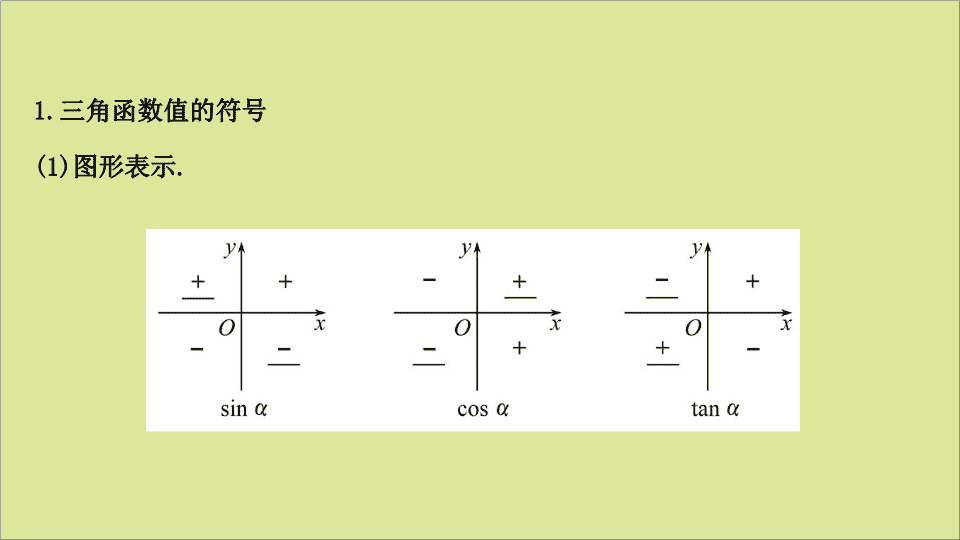
5.2.1 三角函数的概念 ( 二 ) 必备知识 · 自主学习 1. 三角函数值的符号 (1) 图形表示 . (2) 记忆口诀:一全正、二正弦、三正切、四余弦 . (3) 本质:三角函数值在各个象限内的符号,是根据单位圆与角的终边在各个象限内的交点坐标的符号决定的 . (4) 应用:根据三角函数值在各个象限内的符号,可以在不求三角函数值的情况下,判断三角函数的正负 . 2. 公式一 (1) 公式: sin(α+k·2π)=_______ , cos(α+k·2π)=_______ , tan(α+k·2π)=_______(k∈Z). (2) 本质:终边相同的角的终边与单位圆交点相同,因此同一三角函数值相等 . (3) 应用:将角的三角函数转化为终边相同的特殊角的同一三角函数求值 . sin α cos α tan α 【 思考 】 根据三角函数的公式一,终边相同的角的同一三角函数值有何关系? 提示: 终边相同的角,其同一三角函数的值相等 . 【 基础小测 】 1. 辨析记忆 ( 对的打“√”,错的打“ ×”) (1) 已知 α 是三角形的内角,则必有 cos α>0. ( ) (2) 终边相同的角的同一三角函数值相等 . ( ) (3) 若 sin α>0 ,则 α 一定在第一或第二象限 . ( ) 提示: (1) ×. 当 α 为钝角时, cos α<0. (2) √. (3) ×. 终边落在 y 轴的非负半轴上,也有 sin α>0. 2. 若 sin θ·cos θ>0 ,则角 θ 在 ( ) A. 第一或第四象限 B. 第一或第三象限 C. 第一或第二象限 D. 第二或第四象限 【 解析 】 选 B. 因为 sin θ · cos θ>0 ,所以 sin θ>0 , cos θ>0 或 sin θ<0 , cos θ<0 ,所以角 θ 在第一象限或第三象限 . 3.( 教材二次开发:例题改编 )sin(-315°) 的值是 ( ) 【 解析 】 选 C.sin(-315°)=sin(-360°+45°)=sin 45°= . 关键能力 · 合作学习 类型一 三角函数值符号的应用 ( 数学抽象、直观想象 ) 【 题组训练 】 1.(2020 · 珠海高一检测 ) 已知点 M(sin θ , tan θ) 在第三象限,则角 θ 在 ( ) A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限 2.(2020 · 南宁高一检测 ) 若 sin α·cos α<0 ,则角 α 的终边在 ( ) A. 第一或第二象限 B. 第一或第三象限 C. 第一或第四象限 D. 第二或第四象限 3. 判断下列各式的符号: ① tan 191°-cos 191° ; ② sin 3·cos 4·tan 5. 【 解析 】 1. 选 D. 因为点 M(sin θ , tan θ) 在第三象限,所以 由①知, θ 为第三象限、第四象限或 y 轴非正半轴上的角; 由②知, θ 为第二或第四象限角 . 综上,角 θ 在第四象限 . 2. 选 D. 因为 sin α · cos α<0 ,则 sin α>0 , cos α<0 或 sin α<0 , cos α>0. 若 sin α>0 , cos α<0 ,则角 α 的终边在第二象限 . 若 sin α<0 , cos α>0 , 则角 α 的终边在第四象限 . 综上,角 α 的终边在第二或第四象限 . 3.① 正;因为 191° 是第三象限角; 所以 tan 191°>0 , cos 191°<0. 所以 tan 191°-cos 191°>0. ② 正;因为 <3<π , π<4< , <5<2π , 所以 sin 3>0 , cos 4<0 , tan 5<0 , 所以 sin 3 · cos 4 · tan 5>0. 【 解题策略 】 判断三角函数的符号的常用方法 (1) 定象限:根据题目给出的条件,确定角所在的象限 . (2) 定符号:根据角所在象限,结合题目的具体特点,最终确定符号 . 【 补偿训练 】 已知角 α 的终边过点 (3a-9 , a+2) ,且 cos α≤0 , sin α>0 , 则实数 a 的取值范围是 _______. 【 解析 】 因为 cos α≤0 , sin α>0 ,所以角 α 的终边在第二象限或 y 轴非负 半轴上,因为 α 终边过 (3a-9 , a+2) ,所以 所以 -2查看更多