2010-2015高考 全国卷1卷 文科数学试题及答案
2010 年普通高等学校招生全国统一考试
文科数学
参考公式:
样本数据 1 2, nx x x 的标准差 锥体体积公式
2 2 2
1 2
1 ( ) ( ) ( )ns x x x x x xn
1
3V sh
其中 x 为样本平均数 其中 S 为底面面积,h 为高
柱体体积公式 球的表面积,体积公式
V Sh 2 334 , 4S R V R
其中 S 为底面面积,h 为高 其中 R 为球的半径
第Ⅰ卷
一、选择题:本大题共 12 小题,每小题 5 分,在每小题给出的四个选项中,
只有一项是符合题目要求的。[来源:学科网]
(1)已知集合 2, , | 4, |A x x x R B x x x Z ,则 A B
(A)(0,2) (B)[0,2] (C)|0,2| (D)|0,1,2|
(2)a,b 为平面向量,已知 a=(4,3),2a+b=(3,18),则 a,b 夹角的
余弦值等于
(A) 8
65
(B) 8
65
(C) 16
65
(D) 16
65
(3)已知复数 2
3
(1 3 )
iz
i
,则 i =
(A) 1
4
(B) 1
2
(C)1 (D)2
(4)曲线 2y 2 1x x 在点(1,0)处的切线方程为
(A) 1y x (B) 1y x
(C) 2 2y x (D) 2 2y x
(5)中心在远点,焦点在 x 轴上的双曲线的一条渐近线经过点(4,2),则它的离
心率为
(A) 6 (B) 5 (C) 6
2
(D) 5
2
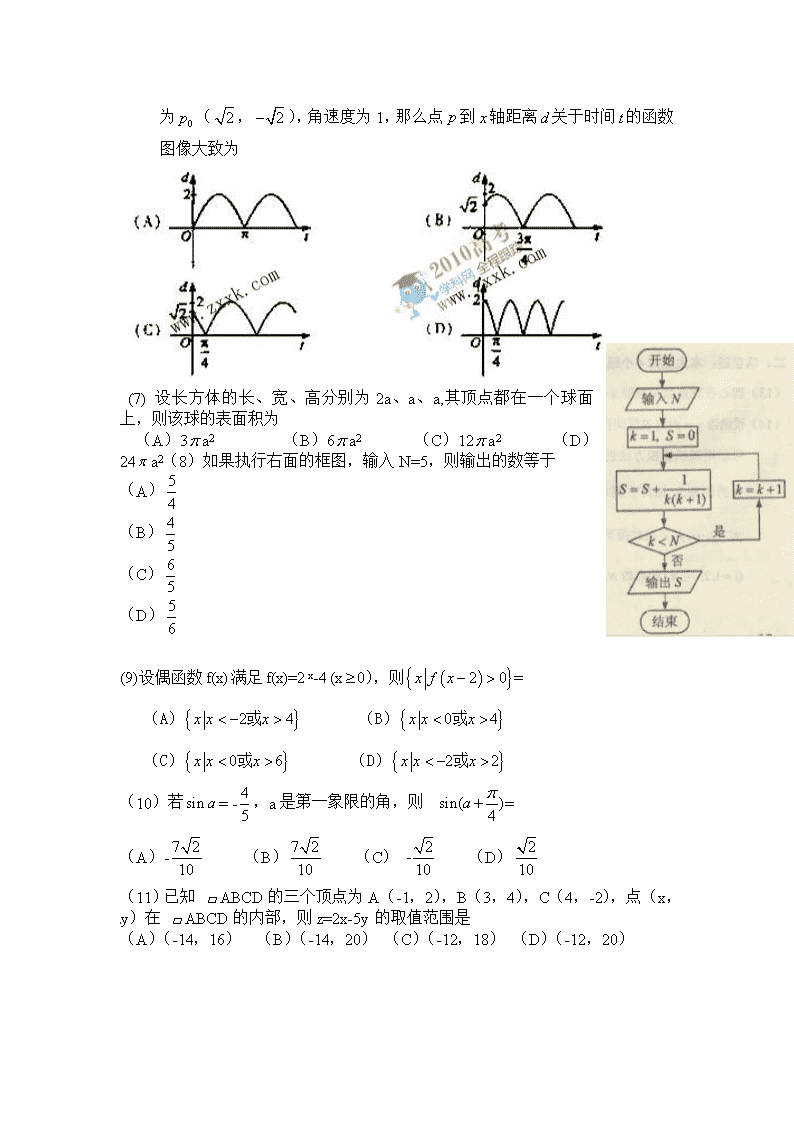
(6)如图,质点 p 在半径为 2 的圆周上逆时针运动,其初始位置
为 0p ( 2 , 2 ),角速度为 1,那么点 p 到 x 轴距离 d 关于
时间t 的函数图像大致为
(7) 设长方体的长、宽、高分别为 2a、a、a,其顶点都在一个球面上,
则该球的表面积为
(A)3 a2 (B)6 a2 (C)12 a2 (D)24 a2
(8)如果执行右面的框图,输入 N=5,则输出的数等于
(A) 5
4
(B) 4
5
(C) 6
5
(D) 5
6
(9)设偶函数 f(x)满足 f(x)=2x-4 (x 0),则 2 0x f x =
(A) 2 4x x x 或 (B) 0 4 x x x 或
(C) 0 6 x x x 或 (D) 2 2 x x x 或
(10)若sin a = - 4
5
,a 是第一象限的角,则 sin( )4a =
(A)- 7 2
10
(B) 7 2
10
(C) 2 - 10
(D) 2
10
(11)已知 ABCD 的三个顶点为 A(-1,2),B(3,4),C(4,-2),点(x,
y)在 ABCD 的内部,则 z=2x-5y 的取值范围是
(A)(-14,16) (B)(-14,20) (C)(-12,18) (D)(-12,20)
(12)已知函数 f(x)=
lg 1,0 10
1 6, 02
x x
x x
若 a,b,c 均不相等,且 f(a)= f(b)= f(c),则
abc 的取值范围是
(A)(1,10) (B)(5,6) (C)(10,12) (D)(20,24)
第Ⅱ卷
本卷包括必考题和选考题两部分。第(13)题~第(21)题为必考题,每个
试题考生都必须做答。第(22)题~第( 24)题为选考题,考生根据要求做答。
二填空题:本大题共 4 小题,每小题 5 分。
(13)圆心在原点上与直线 2 0x y 相切的圆的方程为-----------。
(14)设函数 ( )y f x 为区间 0,1 上的图像是连续不断的一条曲线,且恒有
0 1f x ,可以用随机模拟方法计算由曲线 ( )y f x 及直线 0x , 1x , 0y
所围成部分的面积,先产生两组i 每组 N 个,区间 0,1 上的均匀随机数 1, 2..... nx x x 和
1, 2..... ny y y , 由 此 得 到 V 个 点 , 1,2....x y i N 。 再 数 出 其 中 满 足
1 ( )( 1,2..... )y f x i N 的 点 数 1N 那 么 由 随 机 模 拟 方 法 可 得 S 的 近 似 值 为
___________
(15)一个几何体的正视图为一个三角形,则这个几何体可能是下列几何体中的
_______(填入所有可能的几何体前的编号) ①三棱锥 ②四棱锥 ③三棱
柱 ④四棱柱 ⑤圆锥 ⑥圆柱
(16)在 ABC 中,D 为 BC 边上一点, 3BC BD , 2AD , 135ADB .若
2AC AB ,则 BD=_____
三、解答题:解答应写出文字说明,证明过程或演算步骤。
(17)(本小题满分 12 分)
设等差数列 na 满足 3 5a , 10 9a 。
(Ⅰ)求 na 的通项公式;
(Ⅱ)求 na 的前 n 项和 nS 及使得 nS 最大的序号n 的值。
(18)(本小题满分 12 分)
如图,已知四棱锥 P ABCD 的底面为等腰梯形, AB ∥CD , AC BD ,垂足为
H , PH 是四棱锥的高。
(Ⅰ)证明:平面 PAC 平面 PBD ;
(Ⅱ)若 6AB , APB ADB 60°,求四棱锥 P ABCD 的体积。
请考生在第(22)、(23)、(24)三题中任选一题作答,如果多做,则按所做
的第一题计分。作答时用 2B 铅笔在答题卡上把所选题目的题号涂黑。
(19)(本小题满分 12 分)
为调查某地区老年人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调
查了 500 位老人,结果如下:
(Ⅰ)估计该地区老年人中,需要志愿提供帮助的老年人的比例;
(Ⅱ)能否有 99℅的把握认为该地区的老年人是否需要志愿者提供帮助与性别
有关?
(Ⅲ)根据(Ⅱ)的结论,能否提出更好的调查办法来估计该地区的老年人中,
需要志愿者提供帮助的老年人的比例?说明理由。[来源:学。科。网]
附:
(20)(本小题满分 12 分)
设 1F , 2F 分别是椭圆 E: 2x +
2
2
y
b =1(0﹤b﹤1)的左、右焦点,过 1F 的直线l 与
E 相交于 A、B 两点,且 2AF , AB , 2BF 成等差数列。
(Ⅰ)求 AB
(Ⅱ)若直线l 的斜率为 1,求 b 的值。
(21)本小题满分 12 分)
设函数 21x
xf x e ax
(Ⅰ)若 a= 1
2
,求 xf 的单调区间;[来源:学科网]
(Ⅱ)若当 x ≥0 时 xf ≥0,求 a 的取值范围
(22)(本小题满分 10 分)选修 4—1:几何证明选讲
如图:已知圆上的弧 AC BD ,过 C 点的圆的切线与 BA 的延长线交于
E 点,证明:
(Ⅰ) ACE = BCD 。
(Ⅱ) 2BC =BE x CD。
(23)(本小题满分 10 分)选修 4—4:坐标系与参数方程
已知直线 1C :{ {t 为参数}。图 2C :{ { 为参数}
(Ⅰ)当 a=
3
时,求 1C 与 2C 的交点坐标:
(Ⅱ)过坐标原点 O 做 1C 的垂线,垂足为 A、P 为 OA 的中点,当 a 变
化时,
求 P 点轨迹的参数方程,并指出它是什么曲线。
(
X=1+tcosa
y=tsina
X= cos
y=sin
24)(本小题满分 10 分)选修 4—5:不等式选讲[来源:学科网]
设函数 ( )x = 2 4x + 1。
(Ⅰ)画出函数 y= ( )x 的图像:
(Ⅱ)若不等式 ( )x ≤ax 的解集非空,求 n 的取值范围
2011 年普通高等学校招生全国统一考试文科数学
一、选择题:本大题共 12 小题,每小题 5 分,在每小题给出的四个选项中,只有一项是符
合题目要求的.
1.已知集合 M={0,1,2,3,4},N={1,3,5},P=M N ,则 P 的子集共有
A.2 个 B.4 个 C.6 个 D.8 个
2.复数 5
1 2
i
i
A. 2 i B.1 2i
C. 2 i D. 1 2i
3.下列函数中,既是偶函数又在 (0, ) 单调递增的函数是
A. 3y x B. | | 1y x
C. 2 1y x D. | |2 xy
4.椭圆
2 2
116 8
x y 的离心率为
A. 1
3 B. 1
2
C. 3
3 D. 2
2
5.执行右面的程序框图,如果输入的 N 是 6,那么输出的 p 是
A.120 B. 720
C. 1440 D. 5040
6.有 3 个兴趣小组,甲、乙两位同学各自参加其中一个小组,每位同学参加各个小组的可
能性相同,则这两位同学参加同一个兴趣小组的概率为
A. 1
3 B. 1
2 C. 2
3 D. 3
4
7.已知角 的顶点与原点重合,始边与 x 轴的正半轴重合,终边在直线 2y x 上,则 cos2 =
A. 4
5
B. 3
5
C. 3
5 D. 4
5
8.在一个几何体的三视图中,正视图与俯视图如右图所示,则相应的侧
视图可以为
9.已知直线 l 过抛物线 C 的焦点,且与 C 的对称轴垂直,l 与 C 交于 A,B 两点,| | 12AB ,
P 为 C 的准线上一点,则 ABP 的面积为
A.18 B.24 C. 36 D. 48
10.在下列区间中,函数 ( ) 4 3xf x e x 的零点所在的区间为
A. 1( ,0)4
B. 1(0, )4 C. 1 1( , )4 2 D. 1 3( , )2 4
11.设函数 ( ) sin(2 ) cos(2 )4 4f x x x ,则
A. ( )y f x 在 (0, )2
单调递增,其图象关于直线
4x 对称
B. ( )y f x 在 (0, )2
单调递增,其图象关于直线
2x 对称
C. ( )y f x 在 (0, )2
单调递减,其图象关于直线
4x 对称
D. ( )y f x 在 (0, )2
单调递减,其图象关于直线
2x 对称
12.已知函数 ( )y f x 的周期为 2,当 [ 1,1]x 时 2( )f x x ,那么函数 ( )y f x 的图象
与函数 | lg |y x 的图象的交点共有
A.10 个 B.9 个 C.8 个 D.1 个
二、填空题:本大题共 4 小题,每小题 5 分.
13.已知 a 与 b 为两个不共线的单位向量,k 为实数,若向量 a+b 与向量 ka-b 垂直,则
k=_____________.
14.若变量 x,y 满足约束条件 3 2 9
6 9
x y
x y
,则 2z x y 的最小值是_________.
15. ABC 中, 120 , 7, 5B AC AB ,则 ABC 的面积为_________.
16.已知两个圆锥有公共底面,且两圆锥的顶点和底面的圆周都在同一个球面上.若圆锥底
面面积是这个球面面积的 3
16
,则这两个圆锥中,体积较小者的高与体积较大者的高的
比值为________.
三、解答题:解答应写文字说明,证明过程或演算步骤.
17.(本小题满分 12 分)已知等比数列{ }na 中, 1
1
3a ,公比 1
3q .
(I) nS 为{ }na 的前 n 项和,证明: 1
2
n
n
aS
(II)设 3 1 3 2 3log log logn nb a a a ,求数列{ }nb 的通项公式.
18.(本小题满分 12 分)
如图,四棱锥 P ABCD 中,底面 ABCD 为平行四边形, 60DAB , 2AB AD ,
PD 底面 ABCD.
(I)证明: PA BD ;
(II)设 PD=AD=1,求棱锥 D-PBC 的高.
19.(本小题满分 12 分)
某种产品的质量以其质量指标值衡量,质量指标越大表明质量越好,且质量指标值大于
或等于 102 的产品为优质品.现用两种新配方(分别称为 A 配方和 B 配方)做试验,各生
产了 100 件这种产品,并测量了每产品的质量指标值,得到时下面试验结果:
A 配方的频数分布表
指标值分组 [90,94) [94,98) [98,102) [102,106) [106,110]
频数 8 20 42 22 8
B 配方的频数分布表
指标值分组 [90,94) [94,98) [98,102) [102,106) [106,110]
频数 4 12 42 32 10
(I)分别估计用 A 配方,B 配方生产的产品的优质品率;
(II)已知用 B 配方生产的一种产品利润 y(单位:元)与其质量指标值 t 的关系式为
2, 94
2,94 102
4, 102
t
y t
t
估计用 B 配方生产的一件产品的利润大于 0 的概率,并求用 B 配方生产的上述 100 件产品
平均一件的利润.
20.(本小题满分 12 分)
在平面直角坐标系 xOy 中,曲线 2 6 1y x x 与坐标轴的交点都在圆 C 上.
(I)求圆 C 的方程;
(II)若圆 C 与直线 0x y a 交于 A,B 两点,且 ,OA OB 求 a 的值.
21.(本小题满分 12 分)
已 知 函 数 ln( ) 1
a x bf x x x
, 曲 线 ( )y f x 在 点 (1, (1))f 处 的 切 线 方 程 为
2 3 0x y .
(I)求 a,b 的值;
(II)证明:当 x>0,且 1x 时, ln( ) 1
xf x x
.
请考生在第 22、23、24 三题中任选一题做答,如果多做,则按所做的第一题计分.做
答是用 2B 铅笔在答题卡上把所选题目对应题号下方的方框涂黑.
22.(本小题满分 10 分)选修 4-1:几何证明选讲
如图,D,E分别为 ABC 的边AB,AC上的点,且不与 ABC
的顶点重合.已知 AE 的长为 m,AC 的长为 n,AD,AB 的长是
关于 x 的方程 2 14 0x x mn 的两个根.
(I)证明:C,B,D,E 四点共圆;
(II)若 90A ,且 4, 6,m n 求 C,B,D,E 所在圆
的半径.
23.(本小题满分 10 分)选修 4-4:坐标系与参数方程
在直角坐标系 xOy 中,曲线 1C 的参数方程为 2cos (2 2sin
x
y
为参数),M 为 1C 上
的动点,P 点满足 2OP OM ,点 P 的轨迹为曲线 2C .
(I)求 2C 的方程;
(II)在以 O 为极点,x 轴的正半轴为极轴的极坐标系中,射线
3
与 1C 的异于极点
的交点为 A,与 2C 的异于极点的交点为 B,求|AB|.
24.(本小题满分 10 分)选修 4-5:不等式选讲
设函数 ( ) | | 3f x x a x ,其中 0a .
(I)当 a=1 时,求不等式 ( ) 3 2f x x 的解集.
(II)若不等式 ( ) 0f x 的解集为{x| 1}x ,求 a 的值.
2012 年普通高等学校招生全国统一考试
第Ⅰ卷
一、选择题
1.已知集合 A={x|x2-x-2<0},B={x|-1
b>0)的左、右焦点,P 为直线 x=3a
2
上一点,△F1PF2 是底
角为 30°的等腰三角形,则 E 的离心率为( )
(A)1
2
(B)2
3
(C)3
4
(D)4
5
5.已知正三角形 ABC 的顶点 A(1,1),B(1,3),顶点 C 在第一象限,若点(x,y)在△ABC
内部,则 z=-x+y 的取值范围是( )
(A)(1- 3,2) (B)(0,2)
(C)( 3-1,2) (D)(0,1+ 3)
6.如果执行右边的程序框图,输入正整数 N(N≥2)和实数 a1,a2,…,aN,输出 A,B,则( )
(A)A+B 为 a1,a2,…,aN 的和
(B)A+B
2
为 a1,a2,…,aN 的算术平均数
(C)A 和 B 分别是 a1,a2,…,aN 中最大的数和最小的数
(D)A 和 B 分别是 a1,a2,…,aN 中最小的数和最大的数
7.如图,网格纸上小正方形的边长为 1,粗线画出的是某几何体的三视图,则
此几何体的体积为( )
(A)6 (B)9 (C)12 (D)18
8.平面α截球 O 的球面所得圆的半径为 1,球心 O 到平面α的距离为 2,则此
球的体积为 ( )
(A) 6π (B)4 3π (C)4 6π (D)6 3π
9.已知ω>0,0<φ<π,直线 x=π
4
和 x=5π
4
是函数 f(x)=sin(ωx+φ)图像的两条相邻的
对称轴,则φ=( )
(A)π
4
(B)π
3
(C)π
2
(D)3π
4
10.等轴双曲线 C 的中心在原点,焦点在 x 轴上,C 与抛物线 y2=16x 的准线交于 A,B 两点,
|AB|=4 3,则 C 的实轴长为( )
(A) 2 (B)2 2 (C)4 (D)8
11.当 00)的焦点为 F,准线为 l,A 为 C 上一点,已知以 F 为圆心,FA
为半径的圆 F 交 l 于 B,D 两点。
(I)若∠BFD=90°,△ABD 的面积为 4 2,求 p 的值及圆 F 的方程;
(II)若 A,B,F 三点在同一直线 m 上,直线 n 与 m 平行,且 n 与 C 只有一个公共点,求
坐标原点到 m,n 距离的比值。
C B
A
D
C1
A1
21.设函数 f(x)= ex-ax-2
(Ⅰ)求 f(x)的单调区间
(Ⅱ)若 a=1,k 为整数,且当 x>0 时,(x-k) f´(x)+x+1>0,求 k 的最大值
请考生在第 22,23,24 题中任选一题做答,如果多做,则按所做的第一题计分,
做答时请写清楚题号。
22.(本小题满分 10 分)选修 4-1:几何证明选讲
如图,D,E 分别为△ABC 边 AB,AC 的中点,直线 DE 交△ABC 的
外接圆于 F,G 两点,若 CF//AB,证明:
(Ⅰ)CD=BC;
(Ⅱ)△BCD∽△GBD
23.本小题满分 10 分)选修 4—4;坐标系与参数方程
已知曲线 C1 的参数方程是 x=2cosφ
y=3sinφ
(φ为参数),以坐标原点为极点,x 轴的正半轴为极轴
建立极坐标系,曲线 C2 的极坐标方程是ρ=2.正方形 ABCD 的顶点都在 C2 上,且 A、B、C、
D 以逆时针次序排列,点 A 的极坐标为(2,π
3)
(Ⅰ)求点 A、B、C、D 的直角坐标;
(Ⅱ)设 P 为 C1 上任意一点,求|PA| 2+ |PB|2 + |PC| 2+|PD|2 的取值范围。
24.(本小题满分 10 分)选修 4—5:不等式选讲
已知函数 f(x) = |x + a| + |x-2|.
(Ⅰ)当 a =-3 时,求不等式 f(x)≥3 的解集;
(Ⅱ)若 f(x)≤|x-4|的解集包含[1,2],求 a 的取值范围。
2013 年普通高等学校招生全国统一考试数学文史类
(全国卷 I 新课标)
第Ⅰ卷
一、选择题:本大题共 12 小题,每小题 5 分,在每小题给出的四个选项中,只有一项是符
合题目要求的.
1.(2013 课标全国Ⅰ,文 1)已知集合 A={1,2,3,4},B={x|x=n2,n∈A},则 A∩B=( ).
A.{1,4} B.{2,3} C.{9,16} D.{1,2}
2.(2013 课标全国Ⅰ,文 2) 2
1 2i
1 i
=( ).
A.
11 i2
B.
11+ i2
C.
11+ i2 D.
11 i2
3.(2013 课标全国Ⅰ,文 3)从 1,2,3,4 中任取 2 个不同的数,则取出的 2 个数之差的绝对
值为 2 的概率是( ).
A.
1
2 B.
1
3 C.
1
4 D.
1
6
4.(2013 课标全国Ⅰ,文 4)已知双曲线 C:
2 2
2 2 =1x y
a b
(a>0,b>0)的离心率为 5
2
,则
C 的渐近线方程为( ).
A.y=
1
4 x
B.y=
1
3 x
C.y=
1
2 x
D.y=±x
5.(2013 课标全国Ⅰ,文 5)已知命题 p:∀x∈R,2x<3x;命题 q:∃x∈R,x3=1-x2,则下
列命题中为真命题的是( ).
A.p∧q B. p∧q C.p∧ q D. p∧ q
6.(2013 课标全国Ⅰ,文 6)设首项为 1,公比为 2
3
的等比数列{an}的前 n 项和为
Sn,则( ).
A.Sn=2an-1 B.Sn=3an-2 C.Sn=4-3an D.Sn=3-
2an
7.(2013 课标全国Ⅰ,文 7)执行下面的程序框图,如果输入的 t∈[-1,3],则
输出的 s 属于( ).
A.[-3,4] B.[-5,2]
C.[-4,3] D.[-2,5]
8.(2013 课标全国Ⅰ,文 8)O 为坐标原点,F 为抛物线 C:y2= 4 2x 的焦点,P
为 C 上一点,若|PF|= 4 2 ,则△POF 的面积为( ).
A.2 B. 2 2 C. 2 3 D.4
9.(2013 课标全国Ⅰ,文 9)函数 f(x)=(1-cos x)sin x 在[-π,π]的图像大致为( ).
10.(2013 课标全国Ⅰ,文 10)已知锐角△ABC 的内角 A,B,C 的对边分别为 a,b,c,23cos2A
+cos 2A=0,a=7,c=6,则 b=( ).
A.10 B.9 C.8 D.5
11.(2013 课标全国Ⅰ,文 11)某几何体的三视图如图所示,则该几何体的体积为( ).
A.16+8π
B.8+8π
C.16+16π
D.8+16π
12.(2013 课标全国Ⅰ,文 12)已知函数 f(x)=
2 2 , 0,
ln( 1), 0.
x x x
x x
若
|f(x)|≥ax,则 a 的取值范围是( ).
A.(-∞,0] B.(-∞,1]
C.[-2,1] D.[-2,0]
第Ⅱ卷
二、填空题:本大题共 4 小题,每小题 5 分.
13.(2013 课标全国Ⅰ,文 13)已知两个单位向量 a,b 的夹角为 60°,c=ta+(1-t)b.若
b·c=0,则 t=______.
14.(2013 课标全国Ⅰ,文 14)设 x,y 满足约束条件 1 3,
1 0,
x
x y
则 z=2x-y 的最大值
为______.
15.(2013 课标全国Ⅰ,文 15)已知 H 是球 O 的直径 AB 上一点,AH∶HB=1∶2,AB⊥平面α,
H 为垂足,α截球 O 所得截面的面积为π,则球 O 的表面积为______.
16.(2013 课标全国Ⅰ,文 16)设当 x=θ时,函数 f(x)=sin x-2cos x 取得最大值,则
cos θ=______.
三、解答题:解答应写出文字说明,证明过程或演算步骤.
17.(2013 课标全国Ⅰ,文 17)(本小题满分 12 分)已知等差数列{an}的前 n 项和 Sn 满足
S3=0,S5=-5.
(1)求{an}的通项公式;
(2)求数列
2 1 2 1
1
n na a
的前 n 项和.
18.(2013 课标全国Ⅰ,文 18)(本小题满分 12 分)为了比较两种治疗失眠症的药(分别称为
A 药,B 药)的疗效,随机地选取 20 位患者服用 A 药,20 位患者服用 B 药,这 40 位患者在
服用一段时间后,记录他们日平均增加的睡眠时间(单位:h).试验的观测结果如下:
服用 A 药的 20 位患者日平均增加的睡眠时间:
0.6 1.2 2.7 1.5 2.8 1.8 2.2 2.3 3.2 3.5 2.5 2.6 1.2 2.7 1.5 2.9
3.0 3.1 2.3 2.4
服用 B 药的 20 位患者日平均增加的睡眠时间:
3.2 1.7 1.9 0.8 0.9 2.4 1.2 2.6 1.3 1.4 1.6 0.5 1.8 0.6 2.1 1.1
2.5 1.2 2.7 0.5
(1)分别计算两组数据的平均数,从计算结果看,哪种药的疗效更好?
(2)根据两组数据完成下面茎叶图,从茎叶图看,哪种药的疗效更好?
19.(2013 课标全国Ⅰ,文 19)(本小题满分 12 分)如图,三棱柱 ABC-A1B1C1 中,CA=CB,
AB=AA1,∠BAA1=60°.
(1)证明:AB⊥A1C;
(2)若 AB=CB=2,A1C= 6 ,求三棱柱 ABC-A1B1C1 的体积.
20.(2013 课标全国Ⅰ,文 20)(本小题满分 12 分)已知函数 f(x)=ex(ax+b)-x2-4x,曲
线 y=f(x)在点(0,f(0))处的切线方程为 y=4x+4.
(1)求 a,b 的值;
(2)讨论 f(x)的单调性,并求 f(x)的极大值.
21.(2013 课标全国Ⅰ,文 21)(本小题满分 12 分)已知圆 M:(x+1)2+y2=1,圆 N:(x-1)2
+y2=9,动圆 P 与圆 M 外切并且与圆 N 内切,圆心 P 的轨迹为曲线 C.
(1)求 C 的方程;
(2)l 是与圆 P,圆 M 都相切的一条直线,l 与曲线 C 交于 A,B 两点,当圆 P 的半径最长时,
求|AB|.
请考生在第(22)、(23)、(24)三题中任选一题做答.注意:只能做所选定的题目.如果多做,
则按所做的第一个题目计分,做答时请用 2B 铅笔在答题卡上将所选题号后的方框涂黑.
22.(2013 课标全国Ⅰ,文 22)(本小题满分 10 分)选修 4—1:几何证明选讲
如图,直线 AB 为圆的切线,切点为 B,点 C 在圆上,∠ABC 的角平分线 BE 交圆于点 E,DB
垂直 BE 交圆于点 D.
23.(2013 课标全国Ⅰ,文 23)(本小题满分 10 分)选修 4—4:坐标系与参数方程已知曲线
C1 的参数方程为 4 5cos ,
5 5sin
x t
y t
(t 为参数),以坐标原点为极点,x 轴的正半轴为极轴建立
极坐标系,曲线 C2 的极坐标方程为ρ=2sin θ.
(1)把 C1 的参数方程化为极坐标方程;
(2)求 C1 与 C2 交点的极坐标(ρ≥0,0≤θ<2π).
24.(2013 课标全国Ⅰ,文 24)(本小题满分 10 分)选修 4—5:不等式选讲已知函数 f(x)=
|2x-1|+|2x+a|,g(x)=x+3.
(1)当 a=-2 时,求不等式 f(x)<g(x)的解集;
(2)设 a>-1,且当 x∈ 1,2 2
a
时,f(x)≤g(x),求 a 的取值范围.
2013 年普通高等学校夏季招生全国统一考试数学文史类
(全国卷 I 新课标)
第Ⅰ卷
一、选择题:本大题共 12 小题,每小题 5 分,在每小题给出的四个选项中,只有一项是符
合题目要求的.
1.
答案:A
解析:∵B={x|x=n2,n∈A}={1,4,9,16},
∴A∩B={1,4}.
2.
答案:B
解析: 2
1 2i 1 2i 1 2i i 2 i
1 i 2i 2 2
= 11+ i2
.
3.
答案:B
解析:由题意知总事件数为 6,且分别为(1,2),(1,3),(1,4),(2,3),(2,4),(3,4),满
足条件的事件数是 2,所以所求的概率为 1
3
.
4.
答案:C
解析:∵ 5
2e ,∴ 5
2
c
a
,即
2
2
5
4
c
a
.
∵c2=a2+b2,∴
2
2
1
4
b
a
.∴ 1
2
b
a
.
∵双曲线的渐近线方程为 by xa
,
∴渐近线方程为 1
2y x .故选 C.
5.
答案:B
解析:由 20=30 知,p 为假命题.令 h(x)=x3-1+x2,
∵h(0)=-1<0,h(1)=1>0,
∴x3-1+x2=0 在(0,1)内有解.
∴∃x∈R,x3=1-x2,即命题 q 为真命题.由此可知只有 p∧q 为真命题.故选 B.
6.
答案:D
解析: 11
211 3
21 1 1 3
n n
n
n
aa a qa qS q q
=3-2an,故选 D.
7.
答案:A
解析:当-1≤t<1 时,s=3t,则 s∈[-3,3).
当 1≤t≤3 时,s=4t-t2.
∵该函数的对称轴为 t=2,
∴该函数在[1,2]上单调递增,在[2,3]上单调递减.
∴smax=4,smin=3.
∴s∈[3,4].
综上知 s∈[-3,4].故选 A.
8.
答案:C
解析:利用|PF|= 2 4 2Px ,可得 xP=3 2 .
∴yP= 2 6 .∴S△POF= 1
2
|OF|·|yP|= 2 3 .
故选 C.
9.
答案:C
解析:由 f(x)=(1-cos x)sin x 知其为奇函数.可排除 B.当 x∈ π0, 2
时,f(x)>0,
排除 A.
当 x∈(0,π)时,f′(x)=sin2x+cos x(1-cos x)=-2cos2x+cos x+1.
令 f′(x)=0,得 2 π3x .
故极值点为 2 π3x ,可排除 D,故选 C.
10.
答案:D
解析:由 23cos2A+cos 2A=0,得 cos2A= 1
25
.
∵A∈ π0, 2
,∴cos A= 1
5
.
∵cos A=
236 49
2 6
b
b
,∴b=5 或 13
5b (舍).
故选 D.
11.
答案:A
解析:该几何体为一个半圆柱与一个长方体组成的一个组合体.
V 半圆柱= 1
2
π×22×4=8π,
V 长方体=4×2×2=16.
所以所求体积为 16+8π.故选 A.
12.
答案:D
解析:可画出|f(x)|的图象如图所示.
当 a>0 时,y=ax 与 y=|f(x)|恒有公共点,所以排除 B,C;
当 a≤0 时,若 x>0,则|f(x)|≥ax 恒成立.
若 x≤0,则以 y=ax 与 y=|-x2+2x|相切为界限,
由 2
,
2 ,
y ax
y x x
得 x2-(a+2)x=0.
∵Δ=(a+2)2=0,∴a=-2.
∴a∈[-2,0].故选 D.
第Ⅱ卷
本卷包括必考题和选考题两部分.第 13 题~第 21 题为必考题,每个试题考生都必须做答.第
22 题~第 24 题为选考题,考生根据要求做答.
二、填空题:本大题共 4 小题,每小题 5 分.
13.答案:2
解析:∵b·c=0,|a|=|b|=1,〈a,b〉=60°,∴a·b= 1 11 1 2 2
.
∴b·c=[ta+(1-t)b]·b=0,
即 ta·b+(1-t)b2=0.
∴ 1
2 t +1-t=0.
∴t=2.
14.答案:3
解析:画出可行域如图所示.
画出直线 2x-y=0,并平移,当直线经过点 A(3,3)时,z 取最大
值,且最大值为 z=2×3-3=3.
15.答案: 9 π2
解析:如图,
设球 O 的半径为 R,
则 AH= 2
3
R ,
OH=
3
R .
又∵π·EH2=π,∴EH=1.
∵在 Rt△OEH 中,R2=
2
2+13
R
,∴R2= 9
8
.
∴S 球=4πR2= 9π
2
.
16.答案: 2 5
5
解析:∵f(x)=sin x-2cos x= 5 sin(x-φ),
其中 sin φ= 2 5
5
,cos φ= 5
5
.
当 x-φ=2kπ+ π
2
(k∈Z)时,f(x)取最大值.
即θ-φ=2kπ+ π
2
(k∈Z),θ=2kπ+ π
2
+φ(k∈Z).
∴cos θ= πcos 2
=-sin φ= 2 5
5
.
三、解答题:解答应写出文字说明,证明过程或演算步骤.
17.
解:(1)设{an}的公差为 d,则 Sn= 1
( 1)
2
n nna d .
由已知可得 1
1
3 3 0,
5 10 5,
a d
a d
解得 a1=1,d=-1.
故{an}的通项公式为 an=2-n.
(2)由(1)知
2 1 2 1
1
n na a
= 1 1 1 1
3 2 1 2 2 2 3 2 1n n n n
,
从而数列
2 1 2 1
1
n na a
的前 n 项和为
1 1 1 1 1 1 1
2 1 1 1 3 2 3 2 1n n
=
1 2
n
n
.
18.
解:(1)设 A 药观测数据的平均数为 x ,B 药观测数据的平均数为 y .
由观测结果可得
x = 1
20
(0.6+1.2+1.2+1.5+1.5+1.8+2.2+2.3+2.3+2.4+2.5+2.6+2.7+2.7+
2.8+2.9+3.0+3.1+3.2+3.5)
=2.3,
y = 1
20
(0.5+0.5+0.6+0.8+0.9+1.1+1.2+1.2+1.3+1.4+1.6+1.7+1.8+1.9+
2.1+2.4+2.5+2.6+2.7+3.2)
=1.6.
由以上计算结果可得 x > y ,因此可看出 A 药的疗效更好.
(2)由观测结果可绘制如下茎叶图:
从以上茎叶图可以看出,A 药疗效的试验结果有 7
10
的叶集中在茎 2,3 上,而 B 药疗效的试
验结果有 7
10
的叶集中在茎 0,1 上,由此可看出 A 药的疗效更好.
19.
(1)证明:取 AB 的中点 O,连结 OC,OA1,A1B.
因为 CA=CB,
所以 OC⊥AB.
由于 AB=AA1,∠BAA1=60°,
故△AA1B 为等边三角形,
所以 OA1⊥AB.
因为 OC∩OA1=O,所以 AB⊥平面 OA1C.
又 A1C⊂平面 OA1C,故 AB⊥A1C.
(2)解:由题设知△ABC 与△AA1B 都是边长为 2 的等边三角形,
所以 OC=OA1= 3 .
又 A1C= 6 ,则 A1C2=OC2+ 2
1OA ,
故 OA1⊥OC.
因为 OC∩AB=O,所以 OA1⊥平面 ABC,OA1 为三棱柱 ABC-A1B1C1 的高.
又△ABC 的面积 S△ABC= 3 ,故三棱柱 ABC-A1B1C1 的体积 V=S△ABC×OA1=3.
20.
解:(1)f′(x)=ex(ax+a+b)-2x-4.
由已知得 f(0)=4,f′(0)=4.
故 b=4,a+b=8.
从而 a=4,b=4.
(2)由(1)知,f(x)=4ex(x+1)-x2-4x,
f′(x)=4ex(x+2)-2x-4=4(x+2)· 1e 2
x
.
令 f′(x)=0 得,x=-ln 2 或 x=-2.
从而当 x∈(-∞,-2)∪(-ln 2,+∞)时,f′(x)>0;
当 x∈(-2,-ln 2)时,f′(x)<0.
故 f(x)在(-∞,-2),(-ln 2,+∞)上单调递增,在(-2,-ln 2)上单调递减.
当 x=-2 时,函数 f(x)取得极大值,极大值为 f(-2)=4(1-e-2).
21.
解:由已知得圆 M 的圆心为 M(-1,0),半径 r1=1;圆 N 的圆心为 N(1,0),半径 r2=3.设圆
P 的圆心为 P(x,y),半径为 R.
(1)因为圆 P 与圆 M 外切并且与圆 N 内切,
所以|PM|+|PN|=(R+r1)+(r2-R)=r1+r2=4.
由椭圆的定义可知,曲线 C 是以 M,N 为左、右焦点,长半轴长为 2,短半轴长为 3 的椭圆
(左顶点除外),其方程为
2 2
=14 3
x y (x≠-2).
(2)对于曲线 C 上任意一点 P(x,y),由于|PM|-|PN|=2R-2≤2,
所以 R≤2,当且仅当圆 P 的圆心为(2,0)时,R=2.
所以当圆 P 的半径最长时,其方程为(x-2)2+y2=4.
若 l 的倾斜角为 90°,则 l 与 y 轴重合,可得|AB|= 2 3 .
若 l 的倾斜角不为 90°,由 r1≠R 知 l 不平行于 x 轴,设 l 与 x 轴的交点为 Q,则
1
| |
| |
QP R
QM r
,
可求得 Q(-4,0),所以可设 l:y=k(x+4).
由 l 与圆 M 相切得
2
| 3 |
1
k
k
=1,解得 k= 2
4
.
当 k= 2
4
时,将 2 24y x 代入
2 2
=14 3
x y ,并整理得 7x2+8x-8=0,解得 x1,2=
4 6 2
7
,
所以|AB|= 21 k |x2-x1|=18
7
.
当 k= 2
4
时,由图形的对称性可知|AB|=18
7
.
综上,|AB|= 2 3 或|AB|=18
7
.
请考生在第(22)、(23)、(24)三题中任选一题做答.注意:只能做所选定的题目.如果多做,
则按所做的第一个题目计分,做答时请用 2B 铅笔在答题卡上将所选题号后的方框涂黑.
22.
(1)证明:连结 DE,交 BC 于点 G.
由弦切角定理得,∠ABE=∠BCE.
而∠ABE=∠CBE,
故∠CBE=∠BCE,BE=CE.
又因为 DB⊥BE,
所以 DE 为直径,∠DCE=90°,
由勾股定理可得 DB=DC.
(2)解:由(1)知,∠CDE=∠BDE,DB=DC,
故 DG 是 BC 的中垂线,
所以 BG= 3
2
.
设 DE 的中点为 O,连结 BO,则∠BOG=60°.
从而∠ABE=∠BCE=∠CBE=30°,
所以 CF⊥BF,
故 Rt△BCF 外接圆的半径等于 3
2
.
23.
解:(1)将 4 5cos ,
5 5sin
x t
y t
消去参数 t,化为普通方程(x-4)2+(y-5)2=25,
即 C1:x2+y2-8x-10y+16=0.
将 cos ,
sin
x
y
代入 x2+y2-8x-10y+16=0 得ρ2-8ρcos θ-10ρsin θ+16=0.
所以 C1 的极坐标方程为
ρ2-8ρcos θ-10ρsin θ+16=0.
(2)C2 的普通方程为 x2+y2-2y=0.
由
2 2
2 2
8 10 16 0,
2 0
x y x y
x y y
解得 1,
1
x
y
或 0,
2.
x
y
所以 C1 与 C2 交点的极坐标分别为 π2, 4
, π2, 2
.
24.
解:(1)当 a=-2 时,不等式 f(x)<g(x)化为|2x-1|+|2x-2|-x-3<0.
设函数 y=|2x-1|+|2x-2|-x-3,
则 y=
15 , ,2
12, 1,2
3 6, 1.
x x
x x
x x
其图像如图所示.从图像可知,当且仅当 x∈(0,2)时,y<0.
所以原不等式的解集是{x|0<x<2}.
(2)当 x∈ 1,2 2
a
时,f(x)=1+a.
不等式 f(x)≤g(x)化为 1+a≤x+3.
所以 x≥a-2 对 x∈ 1,2 2
a
都成立.
故
2
a ≥a-2,即 a≤ 4
3
.
从而 a 的取值范围是 41, 3
.
2014 年普通高等学校招生全国统一考试(新课标 I)
文科数学
一.选择题:本大题共 10 小题,每小题 5 分,共 50 分. 在每小题给出的四个选项中,只有
一项是符合题目要求的。
(1) 已知集合 { | 1 3}M x x , { | 2 1}N x x ,则 M N I
A. )1,2( B. )1,1( C. )3,1( D. )3,2(
(2)若 0tan ,则
A. sin 2 0 B. 0cos C. sin 0 D. 02cos
(3)设 iiz
1
1 ,则 || z
A.
2
1 B.
2
2 C.
2
3 D. 2
(4)已知双曲线 )0(13
2
2
2
ay
a
x 的离心率为 2,则 a
A. 2 B.
2
6 C.
2
5 D. 1
(5)设函数 )(),( xgxf 的定义域为 R ,且 )(xf 是奇函数, )(xg 是偶函数,则下列结论中
正确的是
A. )()( xgxf 是偶函数 B. )(|)(| xgxf 是奇函数
C. |)(|)( xgxf 是奇函数 D. |)()(| xgxf 是奇函数
(6)设 FED ,, 分别为 ABC 的三边 ABCABC ,, 的中点,则 FCEB
A. AD B. AD2
1 C. BC2
1 D. BC
(7)在函数① |2|cos xy ,② |cos| xy ,③ )62cos( xy ,④ )42tan( xy 中,
最小正周期为 的所有函数为
A.①②③ B. ①③④ C. ②④ D. ①③
8.如图,网格纸的各小格都是正方形,粗实线画出的事一
个几何体的三视图,则这个几何体是( )
A.三棱锥 B.三棱柱 C.四棱锥 D.四棱柱
9.执行右面的程序框图,若输入的 , ,a b k 分别为 1,2,3,则
输出的 M ( )
A. 20
3
B. 7
2
C. 16
5
D. 15
8
10.已知抛物线 C: xy 2 的焦点为 F , yxA 00, 是 C
上一点, xFA 04
5 ,则 x0
( )
A. 1 B. 2 C. 4 D. 8
(11)设 x , y 满 足 约 束 条 件 ,
1,
x y a
x y
且
z x ay 的最小值为 7,则 a
(A)-5 (B)3
(C)-5 或 3 (D)5 或-3
(12)已知函数 3 2( ) 3 1f x ax x ,若 ( )f x 存在唯
一的零点 0x ,且 0 0x ,则 a 的取值范围是
(A) 2, (B) 1,
(B)(C) , 2 (D) , 1
第 II 卷
二、填空题:本大题共 4 小题,每小题 5 分
(13)将 2 本不同的数学书和 1 本语文书在书架上随机排成一行,则 2 本数学书相邻的概率
为________.
(14)甲、乙、丙三位同学被问到是否去过 A 、 B 、C 三个城市时,
甲说:我去过的城市比乙多,但没去过 B 城市;
乙说:我没去过C 城市;
丙说:我们三人去过同一城市;
由此可判断乙去过的城市为________.
(15)设函数
1
1
3
, 1,
, 1,
xe x
f x
x x
则使得 2f x 成立的 x 的取值范围是________.
(16)如图,为测量山高 MN ,选择 A 和另一座山的山顶C 为测量观测点.从 A 点测得 M
点的仰角 60MAN , C 点的仰角 45CAB 以及 75MAC ;从 C 点测得
60MCA .已知山高 100BC m ,则山高 MN ________ m .
三、解答题:解答应写出文字说明,证明过程或演算步骤.
(17)(本小题满分 12 分)
已知 na 是递增的等差数列, 2a , 4a 是方程 2 5 6 0x x 的根。
(I)求 na 的通项公式;
(II)求数列
2
n
n
a
的前 n 项和.
(18)(本小题满分 12 分)
从某企业生产的某种产品中抽取 100 件,测量这些产品的一项质量指标值,由测量表
得如下频数分布表:
质量指标值分组 [75,85) [85,95) [95,105) [105,115) [115,125)
频数 6 26 38 22 8
(I)在答题卡上作出这些数据的频率分布直方图:
(II)估计这种产品质量指标值的平均数及方差(同一组中的数据用该组区间的中点值
作代表);
(III)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“质量指标值不低
于95的产品至少要占全部产品的80%”的规定?
19(本题满分12分)
如图,三棱柱 111 CBAABC 中,侧面 CCBB 11 为菱形, CB1 的中点为O,且 AO 平
面 CCBB 11 .
(1)证明: ;1 ABCB
(2)若 1ABAC , ,1,601 BCCBB 求三棱柱 111 CBAABC 的高.
20.(本小题满分 12 分)
已知点 )2,2(P ,圆C : 0822 yyx ,过点 P 的动直线l 与圆C 交于 BA, 两点,线段 AB
的中点为 M ,O 为坐标原点.
(1)求 M 的轨迹方程;
(2)当 OMOP 时,求l 的方程及 POM 的面积
21(12 分)
设函数 21ln 12
af x a x x bx a ,曲线 1 1y f x f 在点 , 处的切线斜率
为 0
(1)求 b;
(2)若存在 0 1,x 使得 0 1
af x a
,求 a 的取值范围。
请考生在第 22、23、24 题中任选一题作答,如果多做,则按所做的第一题记分,解答
时请写清题号.
(22)(本小题满分 10 分)选修 4-1,几何证明选讲
如图,四边形 ABCD 是 O 的内接四边形, AB 的延长线与 DC 的延长线交于点 E ,
且CB CE .
(I)证明: D E ;
(II)设 AD 不是 O 的直径, AD 的中点为 M ,且 MB MC ,证明: ABC 为等
边三角形.
(23)(本小题满分 10 分)选修 4-4:坐标系与参数方程
已知曲线 194:
22
yxC ,直线
ty
txl 22
2: (t 为参数)
(1)写出曲线 C 的参数方程,直线l 的普通方程;
(2)过曲线C 上任意一点 P 作与l 夹角为 30°的直线,交l 于点 A ,求 PA 的最大值与最
小值.
(24)(本小题满分 10 分)选修 4-5;不等式选讲
若 ,0,0 ba 且 abba
11
(I)求 33 ba 的最小值;
(II)是否存在 ba, ,使得 632 ba ?并说明理由.
2015 年普通高等学校招生全国统一考试(新课标 1 卷)文
一、选择题:每小题 5 分,共 60 分
1、已知集合 { 3 2, }, {6,8,10,12,14}A x x n n N B ,则集合 A B 中的元素个数为
(A) 5 (B)4 (C)3 (D)2
2、已知点 (0,1), (3,2)A B ,向量 ( 4, 3)AC ,则向量 BC
(A) ( 7, 4) (B) (7,4) (C) ( 1,4) (D) (1,4)
3、已知复数 z 满足 ( 1) 1z i i ,则 z ( )
(A) 2 i (B) 2 i (C) 2 i (D) 2 i
4、如果 3 个正数可作为一个直角三角形三条边的边长,则称这 3 个数为一组勾股数,从
1,2,3,4,5 中任取 3 个不同的数,则这 3 个数构成一组勾股数的概率为( )
(A) 3
10
(B) 1
5
(C) 1
10
(D) 1
20
5、已知椭圆 E 的中心为坐标原点,离心率为 1
2
,E 的右焦点与抛物线 2: 8C y x 的焦点重
合, ,A B 是 C 的准线与 E 的两个交点,则 AB
(A) 3 (B) 6 (C)9 (D)12
6、《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:
“今有委米依垣内角,下周八尺,高五尺,问”积及为米几何?”其意思
为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆
底部的弧长为 8 尺,米堆的高为 5 尺,米堆的体积和堆放的米各位多
少?”已知 1 斛米的体积约为 1.62 立方尺,圆周率约为 3,估算出堆放
的米有( )
(A)14斛 (B) 22 斛 (C)36 斛 (D) 66 斛
7、已知{ }na 是公差为 1 的等差数列, nS 为{ }na 的前 n 项和,若 8 44S S ,则 10a ( )
(A) 17
2
(B)19
2
(C)10 (D)12
8、函数 ( ) cos( )f x x 的部分图像如图所示,则
( )f x 的单调递减区间为( )
(A) 1 3( , ),4 4k k k Z
( B ) 1 3(2 ,2 ),4 4k k k Z ( C )
1 3( , ),4 4k k k Z
(D) 1 3(2 ,2 ),4 4k k k Z
9、执行右面的程序框图,如果输入的 0.01t ,则输出的 n ( )
(A) 5 (B) 6 (C)10 (D)12
10、已知函数
1
2
2 2, 1( )
log ( 1), 1
x xf x
x x
,
且 ( ) 3f a ,则 (6 )f a (A) 4
7
(B) 5
4
(C) 3
4
(D) 1
4
11、圆柱被一个平面截去一部分后与半球(半径为 r )组成一个几何体,该几何体的三视图
中的正视图和俯视图如图所示,若该几何体的表面积为16 20 ,则 r ( )
(A)1
(B) 2
(C) 4
(D)8
12 、 设 函 数 ( )y f x 的 图 像 与 2x ay 的 图 像 关 于 直 线 y x 对 称 , 且
( 2) ( 4) 1f f ,则 a ( ) (A) 1 (B)1 (C)2 (D)
4
二、填空题:本大题共 4 小题,每小题 5 分
13、数列 na 中 1 12, 2 ,n n na a a S 为 na 的前 n 项和,若 126nS ,则 n .
14. 已 知 函 数 3 1f x ax x 的 图 像 在 点 1, 1f 的 处 的 切 线 过 点 2,7 , 则
a .
15. 若 x,y 满足约束条件
2 0
2 1 0
2 2 0
x y
x y
x y
,则 z=3x+y 的最大值为 .
16.已知 P 是双曲线
2
2: 18
yC x 的右焦点,P 是 C 左支上一点, 0,6 6A ,当 APF
周长最小时,该三角形的面积为 .
三、解答题
17. ( 本 小 题 满 分 12 分 ) 已 知 , ,a b c 分 别 是 ABC 内 角 , ,A B C 的 对 边 ,
2sin 2sin sinB A C .
(I)若 a b ,求 cos ;B
(II)若 90B ,且 2,a 求 ABC 的面积.
18.(本小题满分 12 分)如图四边形 ABCD 为菱形,G 为 AC 与 BD 交点,BE ABCD 平面 ,
(I)证明:平面 AEC 平面 BED ;
(II)若 120ABC , ,AE EC 三棱锥 E ACD 的体积为 6
3
,求该三棱锥的侧面
积.
19. (本小题满分 12 分)某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费 x
(单位:千元)对年销售量(单位:t)和年利润 z(单位:千元)的影响,对近 8 年的宣传
费 ix ,和年销售量 1,2,3, ,8iy i 的数据作了初步处理,得到下面的散点图及一些统计
量的值.
(I)根据散点图判断, y a bx 与 y c d x ,哪一个宜作为年销售量 y 关于年宣传
费 x 的回归方程类型(给出判断即可,不必说明理由);
(II)根据(I)的判断结果及表中数据,建立 y 关于 x 的回归方程;
(III)已知这种产品的年利润 z 与 x,y 的关系为 0.2z y x ,根据(II)的结果回答下
列问题:
(i)当年宣传费 90x 时,年销售量及年利润的预报值时多少?(ii)当年宣传费 x 为何值
时,年利润的预报值最大?
20.(本小题满分 12 分)已知过点 1,0A 且斜率为 k 的直线 l 与圆 C: 2 22 3 1x y
交于 M,N 两点.(I)求 k 的取值范围;(II) 12OM ON ,其中 O 为坐标原点,求 MN .
21. (本小题满分 12 分)设函数 2 lnxf x e a x .
(I)讨论 f x 的导函数 f x 的零点的个数;
(II)证明:当 0a 时 22 lnf x a a a
.
请考生在 22、23、24 题中任选一题作答,如果多做,则按所做的第一题计分,作答时请写清题
号
22. (本小题满分 10 分)选修 4-1:几何证明选讲
如图 AB 是圆 O 直径,AC 是圆 O 切线,BC 交圆 O 与点 E.
(I)若 D 为 AC 中点,求证:DE 是圆 O 切线;
(II)若 3OA CE ,求 ACB 的大小.
23. (本小题满分 10 分)选修 4-4:坐标系与参数方程
在直角坐标系 xOy 中,直线 1 : 2C x ,圆 2 2
2 : 1 2 1C x y ,以坐标原点为极
点,x 轴正半轴为极轴建立极坐标系.
(I)求 1 2,C C 的极坐标方程.
(II)若直线 3C 的极坐标方程为 π R4
,设 2 3,C C 的交点为 ,M N ,求 2C MN 的
面积.
24. (本小题满分 10 分)选修 4-5:不等式证明选讲
已知函数 1 2 , 0f x x x a a .
(I)当 1a 时求不等式 1f x 的解集;
(II)若 f x 图像与 x 轴围成的三角形面积大于 6,求 a 的取值范围.