- 2021-04-12 发布 |
- 37.5 KB |
- 20页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
各地小升初数学模拟试卷及解析四川省南充市
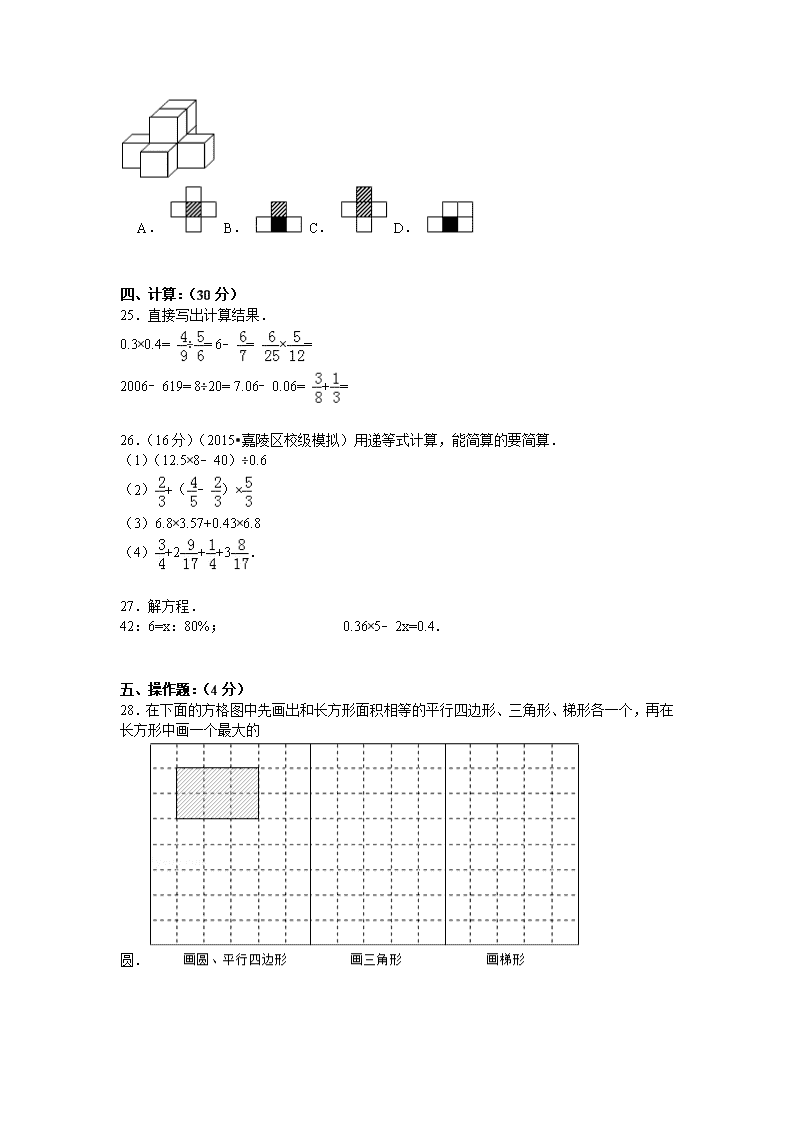
小升初数学模拟试卷及解析 四川省南充市 一、填空:(27分,每空1分) 1.我市今年共接待游客5438700人次,改写成用万作单位的数是 万人次;实现旅游收入三亿七千五百万元,省略亿后面的尾数记作约是 亿. 2.把一根8厘米长的铁丝剪成同样长的5段.每段是全长的 ,每段的长是 厘米. 3. %=3÷4== :20= 小数. 4.时= 时 分 2400毫升= 升. 5.:的比值是 ,把4:1.8化成最简整数比是 : . 6.12和30的最大公约数是 ,最小公倍数是 . 7.比80米多是 米,12千克比15千克少 %. 8.一棵树在照片上高是5厘米,它的实际高度是16米.这张照片的比例尺是 . 9.一项工程甲独做8天完成,乙独做12天完成.甲乙合作 天完成这项工程. 10.王叔叔共上网240小时,其中聊天和学习的比是3:5,他学习占上网时间,聊天 天. 11.一部公交车上,老年乘客的人数约占所有乘客的,学生人数约占,其他青壮年人数约占,问车上 人数最少.如果车上的座位数约是乘客总数的,那么超过的 人不让座,就会有老年乘客站着. 12.△△□☆★△△□☆★△△□☆★…左起第30个是 ,△是 个时,其他三种图形一共是18个. 13.用一根长12厘米长的铁丝围成长方形或正方形(接头处忽略不计),有 种不同的围法(边长取整厘米数).其中面积最大的是 平方厘米. 二、判断题:(正确的打“√”,错误的打“×”.6分,每题1分) 14.作业量一定,已完成的和未完成的不成比例. .(判断对错) 15.两个奇数的和还是奇数. . 16.第29届奥运会于2008年在中国北京举行,这一年的二月份有29天. .(判断对错) 17.100增加20%后,再减少20%,所得的数与原数相等. .(判断对错) 18.用98粒黄豆做发芽实验,结果全部发芽.发芽率是98%. .(判断对错) 19.圆锥体积等于和它等底等高的圆柱体积的 .(判断对错) 三、选择题:(将正确答案前的字母填在括号里.6分,每题1分) 20.王强把1000元按年利率2.25%存入银行.两年后计算他缴纳20%利息税后的实得利息,列式应是( ) A. 1000×2.25%×2×(1﹣20%)+1000 B. [1000×2.25%×(1﹣20%)+1000]×2 C. 1000×2.25%×2×(1﹣20%) 21.投掷3次硬币,有2次正面朝上,1次反面朝上,那么,投掷第4次硬币正面朝上的可能性是( ) A. B. C. D. 22.小军和他的家人居住在面积是110 的房子里,他们在桌面面积是90 的桌子上用餐. A.平方厘米 B.平方分米 C.平方米. 23.参加某次数学竞赛的女生和男生人数的比是1:3,这次竞赛的平均成绩是82分,其中男生的平均成绩是80分,女生的平均成绩是( ) A. 82分 B. 86分 C. 87分 D. 88分 24.如果用表示1个立方体,用表示两个立方体叠加,用表示三个立方体叠加,那么图中由七个立方体叠成的几何体,从正前方观察,可画出的平面图形是( ) A. B. C. D. 四、计算:(30分) 25.直接写出计算结果. 0.3×0.4= ÷= 6﹣= ×= 2006﹣619= 8÷20= 7.06﹣0.06= += 26.(16分)(2015•嘉陵区校级模拟)用递等式计算,能简算的要简算. (1)(12.5×8﹣40)÷0.6 (2)+(﹣)× (3)6.8×3.57+0.43×6.8 (4)+2++3. 27.解方程. 42:6=x:80%; 0.36×5﹣2x=0.4. 五、操作题:(4分) 28.在下面的方格图中先画出和长方形面积相等的平行四边形、三角形、梯形各一个,再在长方形中画一个最大的圆. 六、解决问题:(27分) 29.小明买一套衣服共用去260元,裤子价是上衣的,上衣的价钱是多少元? 30.“小草”文学社假期到无锡太湖边采风.汽车从学校出发,小时行了全程的,这时距离无锡太湖边还有4千米.照这样的速度,行完全程共用多少小时? 31.小刚有一本科技书共60页,第一天看了全书的,第二天看了全书的60%,两天共看了多少页? 32.装订一本书,如果每页排500个字,可以排180页,如果改为每页排600个字,可以少排多少页?(用比例解) 33.小明读一本书,第一天读了全书的,第二天比第一天多读了6页,这时读的页数与剩下的页数的比是5:6,小明再读多少页就能读完这本书? 34.妈妈的茶杯,这样放在桌上.(如图) ①这只茶杯占据桌面的大小是多少平方厘米? ②茶杯一圈装饰带好看吧,那是小明怕烫伤妈妈的手特意贴上的,这条装饰带宽5厘米,面积至少是多少平方厘米?(接头处忽略不计) ③这只茶杯装满水后的体积是多少?(茶杯厚度忽略不计) 参考答案与试题解析 一、填空:(27分,每空1分) 1.我市今年共接待游3客5438700人次,改写成用万作单位的数是 543.87 万人次;实现旅游收入三亿七千五百万元,省略亿后面的尾数记作约是 4 亿. 考点: 整数的读法和写法;整数的改写和近似数. 专题: 整数的认识. 分析: 根据题意,改写成用万作单位的数,把原数的末尾的四个0去掉,写上一个万字即可; 省略亿后面的尾数求近似数,主要是看千位上的数,如果小于5,舍去变0,如果大于或等于与5,要向亿位进1后再舍去变0. 解答: 解:5438700=543.87万; 三亿七千五百万写作: 37500万≈4亿. 故答案为:543.87,4. 点评: 改写成用万作单位的数,也就是去掉个级的四个0,写上一个万字即可;用四舍五入法求近似数,看清舍去部分的最高位上的数,然后再进一步解答即可. 2.把一根8厘米长的铁丝剪成同样长的5段.每段是全长的 ,每段的长是 厘米. 考点: 分数的意义、读写及分类;分数除法. 分析: (1)根据分数的意义,把一根8厘米长的铁丝看作单位“1”,剪成同样长的5段就是平均分成5份,每段是全长的1÷5=;据此写出. (2)求每段的长根据除法的意义用除法计算. 解答: 解:(1)1÷5=; (2)8÷5=(厘米); 故答案为:,. 点评: 本题主要考查分数的意义,求每段长是全长的几分之几用1除以份数得出,求每段的长用除法计算得出. 3. 75 %=3÷4== 15 :20= 0.75 小数. 考点: 比与分数、除法的关系;小数、分数和百分数之间的关系及其转化. 专题: 综合填空题. 分析: 根据与除法的关系3÷4=,再根据分数的基本性质分子、分母都乘8就是;要所比与分数的关系3÷4=3:4,再根据比的基本性质比的前、后项都乘5就是15:20;3÷4=0.75;把0.75的小数点向右移动两位添上百分号就是75%. 解答: 解:75%=3÷4==15:20=0.75. 故答案为:75,32,15,0.75. 点评: 解答此题的关键是3÷4,根据小数、分数、百分数、除法、比之间的关系及分数的基本性质、比的基本性质即可解答. 4.时= 3 时 24 分 2400毫升= 2.4 升. 考点: 体积、容积进率及单位换算;时、分、秒及其关系、单位换算与计算. 分析: 把3时换算成复名数,整数部分就是3时,把时换算成分数,用乘进率60; 把2400毫升换算成升数,用2400除以进率1000. 解答: 解:时=3时24分; 2400毫升=2.4升. 故答案为:3,24,2.4. 点评: 此题考查名数的换算,把高级单位的名数换算成低级单位的名数,就乘单位间的进率,反之,则除以单位间的进率. 5.:的比值是 ,把4:1.8化成最简整数比是 20 : 9 . 考点: 求比值和化简比. 专题: 比和比例. 分析: (1)用比的前项除以后项,所得的商即为比值: (2)根据比的基本性质,即比的前项和后项同时乘或除以一个相同的数(0除外)比值不变,进而把比化成最简比. 解答: 解:(1): =÷ = (2)4:1.8 =(4×5):(1.8×5) =20:9 故答案为:,20,9. 点评: 此题主要考查了化简比和求比值的方法,另外还要注意化简比的结果是一个比,它的前项和后项都是整数,并且是互质数;而求比值的结果是一个商,可以是整数、小数或分数. 6.12和30的最大公约数是 6 ,最小公倍数是 60 . 考点: 求几个数的最大公因数的方法;求几个数的最小公倍数的方法. 分析: 根据最大公约数和最小公倍数的求法可知:最大公约数是这两个数的公有质因数的乘积,最小公倍数是这两个数公有的质因数和各自独有的质因数的乘积,据此把12和30分解质因数,然后据此求出它们的最大公约数和最小公倍数即可. 解答: 解:12=2×2×3, 30=2×3×5, 所以12和30的最大公约数是:2×3=6, 最小公倍数是:2×3×2×5=60; 故答案为:6,60. 点评: 本题主要考查两个数的最大公约数和最小公倍数的求法,注意找准公有的质因数和独有的质因数. 7.比80米多是 120 米,12千克比15千克少 20 %. 考点: 分数乘法;分数除法. 专题: 文字叙述题. 分析: (1)求比80米多是多少,根据求比一个数多几分之几的数是多少,用80乘以(1+)进行解答. (2)求12千克比15千克少百分之几,把15千克看作单位“1”(作除数),也就是求12千克比15千克少的重量占15千克的百分之几,由此列式解答. 解答: 解:(1)80×(1+) =80× =120(米); 答:比80米多是120米. (2)(15﹣12)÷15 =3÷15 =0.2 =20%; 答:12千克比15千克少20%. 故答案为:120,20. 点评: 此题主要考查①求比一个数多几分之几的数是多少,直接用乘法进行解答,②求一个数比另一个数少百分之几,把被比的数量看作单位“1”,用除法解答. 8.一棵树在照片上高是5厘米,它的实际高度是16米.这张照片的比例尺是 1:320 . 考点: 比例尺. 专题: 比和比例. 分析: 根据比例尺的意义作答,即比例尺是图上距离与实际距离的比. 解答: 解:16米=1600厘米, 5:1600=1:320; 答:这张照片的比例尺是1:320. 故答案为:1:320. 点评: 本题主要考查了比例尺的意义,注意图上距离与实际距离的单位要统一. 9.一项工程甲独做8天完成,乙独做12天完成.甲乙合作 4.8 天完成这项工程. 考点: 简单的工程问题. 专题: 工程问题. 分析: 根据工作时间=工作量÷工作效率,用1除以甲乙的工作效率之和,求出甲乙合作多少天完成这项工程即可. 解答: 解: = =4.8(天) 答:甲乙合作4.8天完成这项工程. 故答案为:4.8. 点评: 此题主要考查了工程问题的应用,对此类问题要注意把握住基本关系,即:工作量=工作效率×工作时间,工作效率=工作量÷工作时间,工作时间=工作量÷工作效率,解答此题的关键是求出甲乙的工作效率之和是多少. 10.王叔叔共上网240小时,其中聊天和学习的比是3:5,他学习占上网时间,聊天 3.75 天. 考点: 比的应用. 专题: 比和比例应用题. 分析: 首先分别判断出学习、聊天各占上网时间的几分之几,然后根据分数乘法的意义,用上网的总时间乘以聊天占的分率,求出聊天多少天即可. 解答: 解:他学习占上网时间的=, 240×() =240× =90(小时) 90小时=3.75(天) 答:他学习占上网时间,聊天3.75天. 故答案为:. 点评: 此题此题主要考查了比的应用,以及分数乘法的意义的应用,要熟练掌握,解答此题的关键是分别判断出学习、聊天各占上网时间的几分之几. 11.一部公交车上,老年乘客的人数约占所有乘客的,学生人数约占,其他青壮年人数约占,问车上 老年乘客 人数最少.如果车上的座位数约是乘客总数的,那么超过的 人不让座,就会有老年乘客站着.[来源:学,科,网Z,X,X,K] 考点: 分数大小的比较;分数的加法和减法. 专题: 压轴题. 分析: (1)将通分比较出大小后,就可知道车上哪类人数最少; (2)把乘客总人数看作单位“1”,那么如果老年人全部坐下,就剩下了(﹣)的座位,所以只要超过(﹣)的人不让坐,就有老年人站着. 解答: 解:(1), =, 因为, 所以车上老年人数最少; (2)﹣==; 答:车上老年人数最少,超过的 人不让座,就会有老年乘客站着. 点评: 此题主要考查异分母分数的大小比较,解答时利用假设法让老年人都坐下,则剩余的座位就是非老年人在座着,若超过这些人,就会有老人站着. 12.△△□☆★△△□☆★△△□☆★…左起第30个是 ★ ,△是 12 个时,其他三种图形一共是18个. 考点: 事物的间隔排列规律. 专题: 压轴题. 分析: 根据题干可得这组图形的排列规律是:5个图形一个循环周期,分别按照:△△□☆★的顺序依次排列,(1)由此只要计算得出第30个图形是第几个周期的第几个图形即可解决问题;(2)一个周期中:有2个△,和另外三个图形,此题可以逆推:已知其他三种图形一共是18个.所以是经过了18÷3=6个周期,由此即可求得△的个数. 解答: 解:这组图形的排列规律是:5个图形一个循环周期,分别按照:△△□☆★的顺序依次排列, (1)30÷5=6, 所以第30个图形是第6周期的最后一个图形,与第一个周期的第一个图形相同是★; (2)18÷3=6, 6×2=12(个), 答:左起第30个是★,△是12个时,其他三种图形一共是18个. 故答案为:★;12. 点评: 根据题干得出这组图形的排列周期规律,是解决此类问题的关键. 13.用一根长12厘米长的铁丝围成长方形或正方形(接头处忽略不计),有 3 种不同的围法(边长取整厘米数).其中面积最大的是 9 平方厘米. 考点: 长方形的周长;长方形、正方形的面积. 分析: 只要看(12÷2)可以分成多少组两个整数的和即可知道有多少种围法;其中数值最接近的两个数的乘积最大,利用长方形的面积公式即可求出. 解答: 解:因为12÷2=6=5+1=4+2=3+3, 所以有3种围法; 3×3=9(平方厘米); 答:共有3种围法,其中面积最大的是9平方厘米. 故答案为:3,9. 点评: 解答此题的关键是明白,把12÷2分成多少组两个整数的和,就有多少种围法;长和宽最接近的面积最大. 二、判断题:(正确的打“√”,错误的打“×”.6分,每题1分) 14.作业量一定,已完成的和未完成的不成比例. √ .(判断对错) 考点: 比例的应用. 分析: 根据题意:已完成的和未完成的和一定,而不是比值或积一定. 解答: 解:根据成比例条件,应该是积或比值一定,所以题干说法是对的. 故答案为:√. 点评: 根据正反比例的概念分析判断. 15.两个奇数的和还是奇数. 错误 . 考点: 奇数与偶数的初步认识. [来源:学科网] 专题: 压轴题. 分析: 奇数是指不能被2整除的数,即个位上是1、3、5、7、9的数;要验证两个奇数的和是否还是奇数,可以多举几个例子,再进行判断. 解答: 解:奇数是指不能被2整除的数;例如:两个奇数为1与3,它们的和是4,是偶数; 再如:两个奇数为9与11,它们的和是20,是偶数; 再如:两个奇数为99与191,它们的和是290,是偶数…; 所以两个奇数的和是偶数,不是奇数. 故判断为:错误. 点评: 解决此题要明确奇数的意义,可举几个例子来验证,最终得出两个奇数的和是偶数,不是奇数. 16.第29届奥运会于2008年在中国北京举行,这一年的二月份有29天. 正确 .(判断对错) 考点: 日期和时间的推算. 分析: 用2008除以4,然后判断2008年是闰年还是平年,平年2月份有28天,闰年2月份有29天. 解答: 解:2008÷4=502, 2008年是闰年,这一年2月份有29天. 故答案为:正确. 点评: 本题关键是判断是平年还是闰年,根据“四年一闰,百年不闰,四百年再闰”来判断. 17.100增加20%后,再减少20%,所得的数与原数相等. 错误 .(判断对错) 考点: 百分数的加减乘除运算. 分析: 100增加20%,是把100看做单位“1”,相当于是求100的(1+20%)是多少;再减少20%,是把100增加20%后的数值看做单位“1”,又是求它的(1﹣20%);列式计算出结果再比较. 解答: 解:100×(1+20%)=120, 120×(1﹣20%)=96, 96<100,所得的数比原数小了. 故答案为:错误. 点评: 此题考查一个数先增加百分之几,再减少同样的百分之几,得到的数比原数小了,因为单位“1”不同了,即使分率相同,得数也不同. 18.用98粒黄豆做发芽实验,结果全部发芽.发芽率是98%. 错误 .(判断对错) 考点: 百分数的实际应用. 专题: 压轴题. 分析: 理解发芽率,发芽率是指发芽的种子数占试验种子总数的百分之几,计算方法为:×100%=发芽率,由此列式解答即可. 解答: 解:×100%=100%; 答:发芽率是100%. 故答案为:错误. 点评: 此题属于百分率问题,计算的结果最大值为100%,都是用一部分数量(或全部数量)除以全部数量乘以百分之百,解题的时候不要被表面数字困惑. 19.圆锥体积等于和它等底等高的圆柱体积的 √ .(判断对错) 考点: 圆柱的侧面积、表面积和体积;圆锥的体积. 专题: 压轴题. 分析: 我们知道,一个圆锥的体积是与它等底等高的圆柱体积的,所以原题说法是正确的. 解答: 解:因为,一个圆锥的体积是与它等底等高的圆柱体积的; 所以,原题说法是正确的; 故答案为√. 点评: 此题是考查圆柱和圆锥的关系,在“等底等高”情况下,圆柱和圆锥的体积有“3倍或”的关系. 三、选择题:(将正确答案前的字母填在括号里.6分,每题1分) 20.王强把1000元按年利率2.25%存入银行.两年后计算他缴纳20%利息税后的实得利息,列式应是( ) A. 1000×2.25%×2×(1﹣20%)+1000 B. [1000×2.25%×(1﹣20%)+1000]×2 C. 1000×2.25%×2×(1﹣20%) 考点: 百分数的实际应用. 分析: 银行的利息税是所得利息的20%,而利息=本金×年利率×时间,由此代入数据计算即可,最后拿到的利息是缴纳利息税后的利息,即税后的实得利息=利息×(1﹣20%). 解答: 解:1000×2.25%×2×(1﹣20%), =22.5×2×80%, =45×80%, =36(元); 答:两年后他缴纳20%利息税后的实得利息是36元. 故选:C. 点评: 此题属于利息问题,有固定的计算方法,利息=本金×利率×时间,税后利息=利息×(1﹣20%). 21.投掷3次硬币,有2次正面朝上,1次反面朝上,那么,投掷第4次硬币正面朝上的可能性是( ) A. B. C. D. [来源:学科网ZXXK] 考点: 可能性的大小. 专题: 压轴题. 分析: 可能性大小,就是事情出现的概率,计算方法是:可能性等于所求情况数占总情况数的几分之几,硬币有两面,每一面的出现的可能性都是. 解答: 解:硬币有两面,正面占总面数的,每一面的出现的可能性都是;[来源:学科网] 故选B. 点评: 本题主要考查了可能性大小的计算,可能性等于所求情况数与总情况数之比.不要被数字所困惑. 22.小军和他的家人居住在面积是110 C 的房子里,他们在桌面面积是90 B 的桌子上用餐. A.平方厘米 B.平方分米 C.平方米. 考点: 根据情景选择合适的计量单位. 专题: 长度、面积、体积单位. 分析: 根据生活经验、对面积单位大小的认识和数据的大小,可知计量小军和他的家人居住在面积是110平方米的房子里,他们在桌面面积是90平方分米的桌子上用餐;据此得解. 解答: 解:军和他的家人居住在面积是110平方米的房子里,他们在桌面面积是90平方分米的桌子上用餐; 故答案为:C,B. 点评: 此题考查根据情景选择合适的计量单位,要注意联系生活实际、计量单位和数据的大小,灵活的选择. 23.参加某次数学竞赛的女生和男生人数的比是1:3,这次竞赛的平均成绩是82分,其中男生的平均成绩是80分,女生的平均成绩是( ) A. 82分 B. 86分 C. 87分 D. 88分 考点: 平均数的含义及求平均数的方法;比的意义. 分析: 根据题意,可找出数量间的相等关系:女生的平均成绩×1+男生的平均成绩×3=全班平均成绩×4,设女生的平均成绩是x,列并解方程即可. 解答: 解:设女生的平均成绩是x,因为总成绩不变,由题意得, x×1+3×80=82×(1+3), x+240=328, x=328﹣240, x=88; 或:[82×(1+3)﹣80×3]÷1, =(328﹣240)÷1, =88(分); 答:女生的平均成绩是88分. 故选:D. 点评: 解答此题关键是先求出全班的总成绩和男生的总成绩,然后求出女生的总成绩,进而求出女生的平均成绩. 24.如果用表示1个立方体,用表示两个立方体叠加,用表示三个立方体叠加,那么图中由七个立方体叠成的几何体,从正前方观察,可画出的平面图形是( ) A. B. C. D. 考点: 从不同方向观察物体和几何体. 专题: 压轴题. 分析: 根据题意和图可知,左边和右边各为一个正方体,当中为三个正方体,上面为两个正方体,然后根据题中定义好的表示方法组合在一起即可. 解答: 解:由题意和图可知,左边和右边各为一个正方体,用表示, 当中为三个正方体,用表示, 上面为两个正方体,用表示, 所以答案B是符合题意的, 故选:B. 点评: 此题关键是注意用什么样的小正方形,代表几个小正方体. 四、计算:(30分) 25.直接写出计算结果. 0.3×0.4= ÷= 6﹣= ×= 2006﹣619= 8÷20= 7.06﹣0.06= += 考点: 分数的加法和减法;小数乘法. 专题: 运算顺序及法则. 分析: 根据整数、小数和分数的加减乘除的计算方法进行计算即可. 解答: 解:0.3×0.4=0.12 ÷= 6﹣= ×= 2006﹣619=1387 8÷20=0.4 7.06﹣0.06=7 += 点评: 口算时,注意运算符号和数据,然后再进行计算,小数的口算要注意小数点的位置. 26.(16分)(2015•嘉陵区校级模拟)用递等式计算,能简算的要简算. (1)(12.5×8﹣40)÷0.6 (2)+(﹣)× (3)6.8×3.57+0.43×6.8 (4)+2++3. 考点: 分数的简便计算;小数四则混合运算. 专题: 运算顺序及法则. 分析: (1)先算乘法,再算减法,最后算除法; (2)先算减法,再算乘法,最后算加法; (3)根据乘法分配律进行简算; (4)根据加法交换律和结合律进行简算. 解答: 解:(1)(12.5×8﹣40)÷0.6 =(100﹣40)÷0.6 =60÷0.6 =100; (2)+(﹣)× =+× =+ =; (3)6.8×3.57+0.43×6.8 =6.8×(3.57+0.43) =6.8×4 =27.2; (4)+2++3 =(+)+(2+3) =1+6 =7. 点评: 考查了运算定律与简便运算,四则混合运算.注意运算顺序和运算法则,灵活运用所学的运算定律简便计算. 27.解方程. 42:6=x:80%; 0.36×5﹣2x=0.4. 考点: 解比例;方程的解和解方程. 专题: 比和比例. 分析: (1)根据比例基本性质,两内项之积等于两外项之积,化简方程,再依据等式的性质,方程两边同时除以6求解. (2)先化简,再根据等式的性质,在方程两边同时加2x,再减去0.4,最后再除以2求解. 解答: 解:(1)42:6=x:80% 6x=42×80% 6x=33.6 6x÷6=33.6÷6 x=5.6 (2)0.36×5﹣2x=0.4 1.8﹣2x=0.4 1.8﹣2x+2x=0.4+2x 0.4+2x=1.8 0.4+2x﹣0.4=1.8﹣0.4 2x=1.4 2x÷2=1.4÷2 x=0.7 点评: 本题主要考查学生依据等式的性质,以及比例的基本性质解方程的能力,解方程时注意对齐等号;知识点:比例基本的性质是:两内项之积等于两外项之积. 五、操作题:(4分) 28.在下面的方格图中先画出和长方形面积相等的平行四边形、三角形、梯形各一个,再在长方形中画一个最大的圆. 考点: 画指定面积的长方形、正方形、三角形;画圆. 专题: 压轴题. 分析: 可设方格图中每个小正方形的边长为1个单位长度,则可求出长方形的面积,再根据长方形的面积推算出面积相等的平行四边形、三角形的底和高,以及梯形的上底、下底以及高,再在规定的地方画出即可.对于在长方形中画出面积最大的圆,只要以长方形的较短边为直径画圆即可. 解答: 解:设方格图中每个小正方形的边长为1个单位长度,则图中长方形的长为3,宽为2,所以面积是:3×2=6,由此所画各图的面积都应为6. 对于平行四边形,取底为3,高为2,由平行四边形的面积公式可得,面积=底×高=3×2=6; 对于三角形,取底为3,高为4,由三角形的面积公式,面积=底×高÷2=3×4÷2=6; 对于梯形,取上底为2,下底为4,高为2,由梯形的面积公式, 面积=(上底+下底)×高÷2=(2+4)×2÷2=6; 如下图所示: [来源:学科网] 点评: 解决此题的关键是能正确推导出面积相等的各类图形的底、高以及圆的半径,其实在面积相等的条件下画出的图形的形状不一定相同,只要满足面积相等即可. 六、解决问题:(27分) 29.小明买一套衣服共用去260元,裤子价是上衣的,上衣的价钱是多少元? 考点: 分数除法应用题. 专题: 分数百分数应用题. 分析: 小明买一套衣服共用去260元,裤子价是上衣的,根据分数加法的意义,总价是上衣的1+,根据分数除法的意义,用总价除以总价占上衣价格的分率,即得上衣多少钱. 解答: 解:260÷(1+) =260 =160(元) 答:上衣价格是160元. 点评: 首先根据已知条件求出总价是上衣的几分之几是完成本题的关键. 30.“小草”文学社假期到无锡太湖边采风.汽车从学校出发,小时行了全程的,这时距离无锡太湖边还有4千米.照这样的速度,行完全程共用多少小时? 考点: 简单的行程问题;比例的应用. 分析: 由题意可知:小时所对应的分率是,用对应量除以对应分率,就是行全程的时间. 解答: 解:行全程需要的时间:÷=(小时); 答:行完全程共用小时. 点评: 解答此题的关键是:找清对应量和对应分率,用对应量除以对应分率,即可求出行完全程需要的时间. 31.小刚有一本科技书共60页,第一天看了全书的,第二天看了全书的60%,两天共看了多少页? 考点: 分数乘法应用题. 专题: 压轴题. 分析: 和60%的单位“1”都是全书的页数,先求出第一天和第二天看了全书的几分之几,再根据分数乘法的意义,求出两天共看的页数. 解答: 解:60×(+60%), =60×0.8, =48(页); 答:两天共看48页. 点评: 解答此题的关键是,找准单位“1”,找出对应量,根据基本的数量关系解决问题. 32.装订一本书,如果每页排500个字,可以排180页,如果改为每页排600个字,可以少排多少页?(用比例解) 考点: 比例的应用. 分析: 根据题意知道此书的总页数一定,每页排字的个数和总页数成反比例,由此列式解答即可. 解答: 解:设改为每页排600个字,可以排x页, 500×180=600×x, 6x=900, x=150, 180﹣150=30(页); 答:可以少排30页. 点评: 解答此题的关键是,先判断题中的两种相关联的量成何比例,再列比例解答. 33.小明读一本书,第一天读了全书的,第二天比第一天多读了6页,这时读的页数与剩下的页数的比是5:6,小明再读多少页就能读完这本书? 考点: 分数四则复合应用题. 专题: 压轴题. 分析: 根据读的页数与剩下的页数的比是5:6,求出总份数为:(5+6)份,又知前两天读了这本书的多6页,占这本书总页数的 ,这样就可以求出6页占这本书总页数的几分之几,再根据已知比一个数少几分之几的数是多少求这个数,求出总页数,再根据一个数乘分数的意义列式用解答. 解答: 解:总份数:5+6=11(份),两天读的占总页数的; 6÷(2)× =6÷()× =6÷× =6×× =60(页); 答:小明再读60页就能读完这本书. 点评: 此题解答关键是把比转化为分数,求出6页所对应的分率,根据已知比一个数少几分之几的数是多少求这个数,和一个乘分数的意义解答. 34.妈妈的茶杯,这样放在桌上.(如图) ①这只茶杯占据桌面的大小是多少平方厘米? ②茶杯一圈装饰带好看吧,那是小明怕烫伤妈妈的手特意贴上的,这条装饰带宽5厘米,面积至少是多少平方厘米?(接头处忽略不计) ③这只茶杯装满水后的体积是多少?(茶杯厚度忽略不计) 考点: 关于圆柱的应用题. 专题: 立体图形的认识与计算. 分析: ①茶杯占据桌面的大小,就是这个圆柱茶杯的底面积是多少,利用圆的面积公式即可解得. ②根据圆柱的侧面展开图的特点,装饰带的面积,就是求出底面直径为8厘米,高为5厘米的圆柱的侧面积.根据侧面积=底面周长×高即可解得. ③这只茶杯装满水后的体积,根据茶杯的容积=底面积×高解答即可. 解答: 解:①3.14×(6÷2)2 =3.14×9 =28.26(平方厘米) ②3.14×6×5=94.2(平方厘米) ③28.26×15=423.9(立方厘米); 答:茶杯占据桌面的面积是28.26平方厘米,装饰带的面积是94.2平方厘米,茶杯的容积是423.9立方厘米. 点评: 此题考查了圆柱的底面积、侧面积与容积公式在实际问题中的灵活应用. 查看更多