- 2021-02-26 发布 |
- 37.5 KB |
- 17页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
小升初数学模拟试卷及解析(32)人教新课标
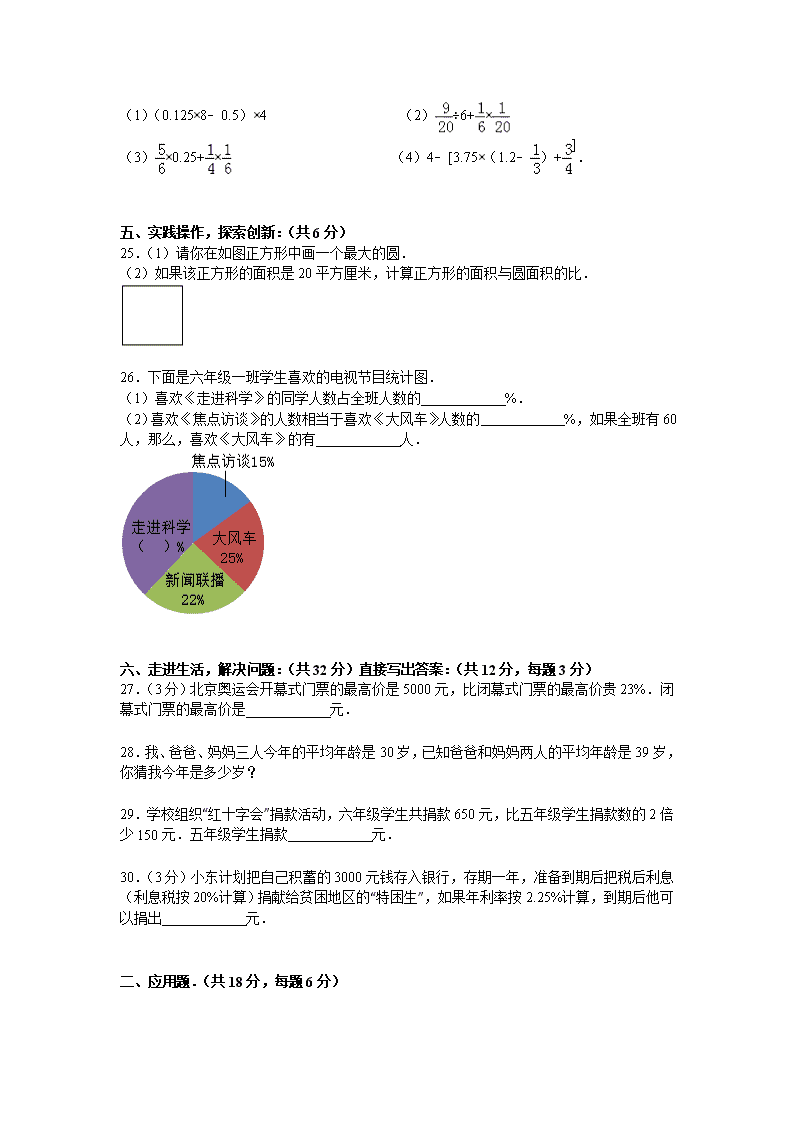
小升初数学模拟试卷及解析(32)|人教新课标(2014 秋) 一、用心思考,正确填写:(共 22 分,每空 1 分) 1.2008 年 8 月 8 日,北京成功举办了第 29 届奥运会,全球约有 4120500000 人收看了电视 转播,改写成以“万人”作单位是 万人,省略亿位后的尾数约是 亿 人. 2.(3 分)20: = ÷45=八折= %. 3.(3 分)1.7 吨= 吨 千克. [来源:Z§xx§k.Com] 8500 毫升= 升. 4.(3 分)用 6、12、15 和 30 这四个数组成一个比例是 . 5.(3 分)某地区高度每增加 100m,气温下降 0.6℃,小明和小红分别在山脚和山顶同时测 得气温分别是 6℃和﹣1.2℃,山高 m. 6.(3 分)一个圆柱侧面展开是一个边长为 9.42dm 的正方形,圆柱体底面直径是 dm,圆柱的高是 dm. 7.(3 分)一个圆柱的体积是 80m3,底面积是 16㎡,它的高是 m. 8.商场有电视机 m 台,每台进价为 a 元,售价 b 元,若全部出售,共可获利 元. 9.一个棱长为 6 分米的正方体木块的表面积是 平方分米,把它切削成一个最 大的圆锥体,这个圆锥体的体积是 立方分米. 10.在比例尺是 1:4000000 的地图上,3 厘米长的线段表示实际距离 千米. 11.下面是长江小学六(1)班第一小组女生的身高记录单. 编号 1 2 3 4 5 6 7 身高/cm 141 141 143 154 145 144 175 (1)这组女生身高的平均数是 ;中位数是 ;众数是 . (2)用 数代表这组女生的身高比较合适. 二、仔细推敲,辨析正误:(对的在括号里打“√”、错的打“×”,共 8 分,每题 2 分) 12.除 2 以外所有的质数都是奇数. .(判断对错) 13.x、y 是两种相关联的量,若 3x=5y,则 x、y 成反比例. .(判断对错) 14.一个长方形的长和宽各增加 3 米,它的面积就增加 9 平方米. .(判断对 错) 15.李师傅做 105 个零件,全部合格,则合格率是 105%. .(判断对错) 三、反复比较,慎重选择:(填正确答案的序号,共 12 分,每题 2 分) 16.世界上第一个把圆周率的值计算精确到六位小数的人是( ) A. 华罗庚 B. 张衡 C. 祖冲之 D. 陶行知 17.(2 分)等腰直角三角形三个内角度数之比是( ) A. 1:2:2 B. 2:1:1 C. 3:2:1 18.一件商品,先提价 20%,以后又降价 20%,现在的价格与原来相比( ) A. 提高了 B. 降低了 C. 不变 D. 无法确定 19.原价每袋 2 元的某种牛奶,正在搞促销活动,甲商店每袋降价 15%,乙商店“买四送 一”,丙商店每袋打八八折出售.小明要买 5 袋牛奶,从( )商店买便宜. A. 甲 B. 乙 C. 丙 D. 无法确定 20.任意转动转盘指针,结果指针( )停在阴影部分. A. 一定 B. 很可能 C. 不可能 21.《快乐大本营》童装店以 100 元卖出两套不同的童装,结果一套赚 20%,一套亏本 20%,总的来说,这个童装店是( ) A. 亏本 B. 赚钱 C. 不亏也不赚 四、看清题目,巧思妙算:(共 22 分) 22.(4 分)直接写出得数. 14÷35= 125+175= 0.77+0.33= 45×4+4×55= 4.36×0= 23.(12 分)(2010•邢台)用递等式计算下面各题: (1)(0.125×8﹣0.5)×4 (2) ÷6+ × (3) ×0.25+ × (4)4﹣[3.75×(1.2﹣ )+ ]. 五、实践操作,探索创新:(共 6 分) 25.(1)请你在如图正方形中画一个最大的圆. (2)如果该正方形的面积是 20 平方厘米,计算正方形的面积与圆面积的比. 26.下面是六年级一班学生喜欢的电视节目统计图. (1)喜欢《走进科学》的同学人数占全班人数的 %. (2)喜欢《焦点访谈》的人数相当于喜欢《大风车》人数的 %,如果全班有 60 人,那么,喜欢《大风车》的有 人. 六、走进生活,解决问题:(共 32 分)直接写出答案:(共 12 分,每题 3 分) 27.(3 分)北京奥运会开幕式门票的最高价是 5000 元,比闭幕式门票的最高价贵 23%.闭 幕式门票的最高价是 元. 28.我、爸爸、妈妈三人今年的平均年龄是 30 岁,已知爸爸和妈妈两人的平均年龄是 39 岁, 你猜我今年是多少岁? 29.学校组织“红十字会”捐款活动,六年级学生共捐款 650 元,比五年级学生捐款数的 2 倍 少 150 元.五年级学生捐款 元. 30.(3 分)小东计划把自己积蓄的 3000 元钱存入银行,存期一年,准备到期后把税后利息 (利息税按 20%计算)捐献给贫困地区的“特困生”,如果年利率按 2.25%计算,到期后他可 以捐出 元. 二、应用题.(共 18 分,每题 6 分) 31.张师傅加工一批零件,第一天完成的个数与零件的总个数的比是 1:3.如果再加工 15 个,就可以完成这批零件的一半.这批零件共有多少个? 32.星期天,小华请 8 名同学到家作客,他妈妈用一盒长方体包装的饮料招待同学.这个长 方体盒子长 15 厘米,宽 12 厘米,高 20 厘米,给每个同学倒了一满杯,杯子的底面积是 50.24 平方厘米,高是 8 厘米,招待客人后,小华他自己还有饮料喝吗?(写出计算过程) 33.武汉移动通信公司推出两种手机卡,采用的收费标准见下表: 种类 固定月租费 每分通话费 A 卡 16 元 0.12 元 B 卡 0 元 0.3 元 妈妈每月的通话时间累计一般在 60 分左右,爸爸每月的通话时间累计一般在 200 分左右, 请你帮助他们分别选一种比较合算的手机卡,并通过计算说明你的理由. 参考答案与试题解析 一、用心思考,正确填写:(共 22 分,每空 1 分) 1.2008 年 8 月 8 日,北京成功举办了第 29 届奥运会,全球约有 4120500000 人收看了电视 转播,改写成以“万人”作单位是 412050 万人,省略亿位后的尾数约是 41 亿人. 考点: 整数的改写和近似数. 分析: (1)改成用“万”作单位的数,是把万位后面的 4 个“0”去掉,或者在万位数的右下 角点上小数点,然后把小数末尾的 0 去掉,再在数的后面写上“万”字,据此改写; (2)省略“亿”后面的尾数就是四舍五入到亿位,就是把亿位后面的千万位上的数进行四舍 五入,再在数的后面写上“亿”字,据此写出. 解答: 解:4120500000=412050 万, 4120500000≈41 亿; 故答案为:412050,41. 点评: 本题主要考查整数的改写和求近似数,注意改写和求近似数时要带计数单位. 2.(3 分)20: 25 = 36 ÷45=八折= 80 %. [来源:学|科|网 Z|X|X|K] 考点: 比与分数、除法的关系. 专题: 比和比例. 分析: 根据折扣的意义八折就是 80%;把 80%化成分数并化简是 ,根据比与分数的关系 =4:5,再根据比的基本性质比的前、后项都乘 5 就是 20:25;根据分数与除法的关系 =2÷5,再根据商不变的性质被除数、除数都乘 9 就是 36÷45. 解答: 解:20:25=36÷45=八折=80%. 故答案为:25,36,80. 点评: 解答此题的关键是八折,根据折扣、小数、分数、百分数、除法、比之间的关系及 分数的基本性质、比的基本性质、商不变的性质即可解答. 3.(3 分)1.7 吨= 1 吨 700 千克. 8500 毫升= 8.5 升. 考点: 体积、容积进率及单位换算;质量的单位换算. 专题: 长度、面积、体积单位;质量、时间、人民币单位. 分析: (1)1.7 吨看作 1 吨与 0.7 吨之和,把 0.7 吨乘进率 1000 化成 700 千克. (2)低级单位毫升化高级单位升除以进率 1000. 解答: 解:(1)1.7 吨=1 吨 700 千克. (2)8500 毫升=8.5 升. 故答案为:1,700,8.5. 点评: 本题是考查质量的单位换算、体积、容积的单位换算.单位换算首先要弄清是由高 级单位化低级单位还是由低级单位化高级单位,其次记住单位间的进率. 4.(3 分)用 6、12、15 和 30 这四个数组成一个比例是 6:12=15:30 . 考点: 比例的意义和基本性质. 专题: 比和比例. 分析: 比例的性质:两个内项的积等于两个外项的积.因为 6×30=12×15,所以如果 6 和 30 当比例的两个外项,则 12 和 15 就当比例的两个内项,反之也可以.据此写出比例即可. 解答: 解:因为 6×30=12×15, 所以可以组成的比例:6:12=15:30(答案不唯一); 故答案为:6:12=15:30(答案不唯一). 点评: 此题属于考查比例性质的运用:根据给出的数,先用它们写出等式,再进一步改写 成比例即可. 5.(3 分)某地区高度每增加 100m,气温下降 0.6℃,小明和小红分别在山脚和山顶同时测 得气温分别是 6℃和﹣1.2℃,山高 1200 m. 考点: 正、负数的运算. 专题: 简单应用题和一般复合应用题. 分析: 首先求出山脚和山顶的温差是多少,再用它除以 0.6,求出某地区高度是 100m 的多 少倍;然后用它乘以 100,求出山高是多少即可. 解答: 解:[6﹣(﹣1.2)]÷0.6×100 =7.2÷0.6×100 =12×100 =1200(m) 答:山高 1200m. 故答案为:1200. 点评: 此题主要考查了正、负数的运算,解答此题的关键是求出山脚和山顶的温差是多 少. 6.(3 分)一个圆柱侧面展开是一个边长为 9.42dm 的正方形,圆柱体底面直径是 3 dm, 圆柱的高是 9.42 dm. 考点: 圆柱的展开图;圆柱的侧面积、表面积和体积. 专题: 立体图形的认识与计算. 分析: 根据圆柱侧面展开图的特征,如果已知的侧面展开是一个正方形,那么它的底面周 长和高相等,根据圆的周长公式即可求出底面直径. 解答: 解:圆柱的侧面展开是一个边长 9.42 分米的正方形,说明这个圆柱的底面周长和高 都是 9.42 分米, 9.42÷3.14=3(分米), 答:圆柱的底面直径是 3 分米,高是 9.42 分米. 故答案为:3 分米,9.42 分米. 点评: 此题考查的目的是理解掌握圆柱侧面展开图的特征,以及圆的周长公式的灵活运 用. 7.(3 分)一个圆柱的体积是 80m3,底面积是 16㎡,它的高是 5 m. 考点: 圆柱的侧面积、表面积和体积. 专题: 立体图形的认识与计算. 分析: 因为圆柱的体积=底面积×高,所以圆柱的高=体积÷底面积,据此解答. 解答: 解:80÷16=5(米), 答:圆柱的高是 5 米. 故答案为:5. 点评: 此题主要考查圆柱体积公式的灵活运用.关键是熟记公式. 8.商场有电视机 m 台,每台进价为 a 元,售价 b 元,若全部出售,共可获利 m(b﹣a) 元. 考点: 用字母表示数. 专题: 用字母表示数. 分析: 用售价减去进价求出每台电视机获利的钱数,再乘 m 求出全部出售共获利的钱 数. 解答: 解:(b﹣a)×m=m(b﹣a)(元), 答:共获利 m(b﹣a)元, 故答案为:m(b﹣a). 点评: 关键是明白售价﹣进价=获利的钱数,进而求出全部出售共获利的钱数. 9.一个棱长为 6 分米的正方体木块的表面积是 216 平方分米,把它切削成一个最大的圆 锥体,这个圆锥体的体积是 56.52 立方分米. 考点: 长方体和正方体的表面积;圆锥的体积. 专题: 压轴题. 分析: 正方体的表面积=棱长×棱长×6,圆锥体的体积=底面积×高;在正方形中最大的圆的 直径等于正方形的边长,由此可以求出圆锥的底面积,从而解决问题. 解答: 解:6×6×6=216 平方分米, 圆锥的底面积为:3.14×(6÷2)2=3.14×9=28.26(平方分米); 圆锥的体积为 ×28.26×6=56.52(立方分米); 故答案为:216,56.52. 点评: 此题理解正方形中最大的圆的直径等于正方形的边长是关键. 10.在比例尺是 1:4000000 的地图上,3 厘米长的线段表示实际距离 120 千米. 考点: 图上距离与实际距离的换算(比例尺的应用). 专题: 压轴题. 分析: 要求 3 厘米表示的实际距离是多少千米,根据“图上距离÷比例尺=实际距离”,代入 数值,计算即可. 解答: 解:3÷ , =3×4000000, =12000000(厘米), 12000000 厘米=120(千米); 答:3 厘米长的线段表示实际距离是 120 千米; 故答案为:120. 点评: 解答此题的关键是根据图上距离、比例尺和实际距离三者的关系,进行分析解答即 可得出结论. 11.下面是长江小学六(1)班第一小组女生的身高记录单. 编号 1 2 3 4 5 6 7 身高/cm 141 141 143 154 145 144 175 (1)这组女生身高的平均数是 149 ;中位数是 144 ;众数是 141 . (2)用 中位 数代表这组女生的身高比较合适. 考点: 简单的统计表;中位数的意义及求解方法. 专题: 压轴题. 分析: 根据求平均数、中位数和众数的方法进行解答.数据的个数(即人数)是偶数个, 求中位数的方法是;把数据按大小顺序排列后中间的数即是.由此解答. 解答: 解:求平均数: (141+141+143+154+145+144+175)÷7 =1043÷7[来源:学科网] =149; 中位数是:144; 众数是:141; 答:(1)这组女生身高的平均数是 149;中位数是 144;众数是 141; (2)用中位数代表这组女生的身高比较合适; 故答案为:(1)149,144,141,(2)中位. 点评: 此题考差点目的是:理解和掌握平均数、中位数和众数的意义及求法,掌握平均数 和中位数的区别. 二、仔细推敲,辨析正误:(对的在括号里打“√”、错的打“×”,共 8 分,每题 2 分) 12.除 2 以外所有的质数都是奇数. 正确 .(判断对错) 考点: 奇数与偶数的初步认识;合数与质数. 分析: 质数是除了一和本身以外没有别的约数. 解答: 解:因为二是最小的质数,除 2 以外所有的质数都是奇数. 故此题答案正确. 点评: 此题考查目的是:①质数的定义.②奇数的定义.③质数与奇数的区别. 13.x、y 是两种相关联的量,若 3x=5y,则 x、y 成反比例. 错误 .(判断对错) 考点: 正比例和反比例的意义. 专题: 压轴题. 分析: 判定两种相关联的量是否成正、反比例,要看这两种量是对应的比值一定,还是对 应的乘积一定,如果是比值一定就成正比例;如果是乘积一定就成反比例. 解答: 解:因为 3x=5y,所以 x÷y= (一定),是比值一定,所以 x、y 成正比例,不成反 比例; 故答案为:错误. 点评: 此题属于根据正、反比例的意义,判断两种相关联的量是成正比例还是成反比例, 就看两种量是对应的比值一定,还是对应的乘积一定,再做出解答. 14.一个长方形的长和宽各增加 3 米,它的面积就增加 9 平方米. × .(判断对错) 考点: 长方形、正方形的面积. 专题: 压轴题. 分析: 分析“一个长方形的长和宽各增加 3 米”这个条件后可知,解答这道题可以用假设法, 也就是举例子,把长方形原来的长和宽看成一个具体的数,然后再表示出增加后长方形的长 和宽,据此根据长方形的面积公式算出它们的面积,再用减法算出面积增加多少平方米,然 后相互比较得出答案. 解答: 解:假设长方形的长是 2 米,宽是 1 米,则这个长方形的长和宽各增加 3 米后,长 是 5 米,宽是 4 米. 则原来长方形的面积 S=ab=2×1=2(平方米), 增加后长方形的面积 S=ab=5×4=20(平方米), 20﹣2=18(平方米); 则“一个长方形的长和宽各增加 3 米,它的面积就增加 9 平方米”这种说法不正确. 故答案为:×. 点评: 像这种题干中没有明确数字的题目,我们可以采用假设法,放到具体的数字中去比 较. 15.李师傅做 105 个零件,全部合格,则合格率是 105%. 错误 .(判断对错) 考点: 百分率应用题. 专题: 压轴题. 分析: 求合格率,根据公式:合格率= ×100%,代入数值,解答求出合格率, 进而判断即可. 解答: 解: ×100%=100%; 答:合格率是 100%. 故答案为:错误. 点评: 此题属于百分率问题,最大值为 100%,解答时都是用一部分数量(或全部数量) 除以全部数量乘以百分之百即可,解答时不要被表面数字所迷惑. 三、反复比较,慎重选择:(填正确答案的序号,共 12 分,每题 2 分) 16.世界上第一个把圆周率的值计算精确到六位小数的人是( ) A. 华罗庚 B. 张衡 C. 祖冲之 D. 陶行知 考点: 圆的认识与圆周率. 分析: 根据课本上“你知道吗”介绍的关于圆周率的相关内容选出即可. 解答: 解:祖冲之(公元 429﹣500 年).他研究圆周率,得出其值就在 3.1415926 与 3.1415927 之间,准确到小数点后 7 位,成为世界上第一个把圆周率的值精确到 7 位小数的人. 故选:C. 点评: 此题考查关于圆周率的历史,培养学生民族自豪感. 17.(2 分)等腰直角三角形三个内角度数之比是( ) A. 1:2:2 B. 2:1:1 C. 3:2:1 考点: 等腰三角形与等边三角形;比的意义;三角形的内角和. 专题: 平面图形的认识与计算. 分析: 根据等腰直角三角形的特点,可知它的三个内角度数分别为 90°、45°和 45°,写出它 们的比,进而根据比的性质把比化成最简比即可. 解答: 解:一个等腰直角三角形,它的三个内角的度数分别为 90°、45°和 45°, 它的三个内角度数的比是:90°:45°:45°=2:1:1. 故选:B. 点评: 解决此题关键是明确一个等腰直角三角形,它的三个内角的度数分别是多少;也考 查了比的性质的运用. 18.一件商品,先提价 20%,以后又降价 20%,现在的价格与原来相比( ) A. 提高了 B. 降低了 C. 不变 D. 无法确定 考点: 百分数的实际应用. 专题: 压轴题;分数百分数应用题. 分析: 设商品的原价是 1,先把原价看成单位“1”,提价 20%后的价格是原价的 1+20%,由 此用乘法求出提价后的价格;再把提价后的价格看成单位“1”,现价是提价后的 1+20%,再 用乘法求出现价,然后现价和原价比较即可判断. 解答: 解:设商品的原价是 1,现价是: 1×(1+20%)×(1﹣20%), =1×120%×80%, =0.96; 0.96<1,现价比原价降低了; 故选:B. 点评: 本题关键是对两个不同单位“1”的理解,进一步发现比单位“1”多或少百分之几,由 此解决问题. 19.原价每袋 2 元的某种牛奶,正在搞促销活动,甲商店每袋降价 15%,乙商店“买四送 一”,丙商店每袋打八八折出售.小明要买 5 袋牛奶,从( )商店买便宜. A. 甲 B. 乙 C. 丙 D. 无法确定 考点: 百分数的实际应用. 专题: 压轴题. 分析: 甲店:降价 15%,是把原价看成单位“1”,现价是原价的(1﹣15%),由此求出 5 袋 的现价; 乙店:买四赠一,买五袋牛奶只需要付 4 袋的钱即可,由此求出 5 袋的现价; 丙店:打八八折是指现价是原价的 88%,把原价看成单位“1”,由此求出 5 袋的现价. 解答: 解:甲店:(2×5)×(1﹣15%), =10×85%, =8.5(元); 乙店:2×4=8(元); 丙店:(2×5)×88%, =10×88%, =8.8(元); 8<8.5<8.8. 所以乙店最便宜. 故选:B. 点评: 先理解三个商店的优惠方法,再根据优惠的方法求出买 5 袋各需多少钱,进而求 解. 20.任意转动转盘指针,结果指针( )停在阴影部分. A. 一定 B. 很可能 C. 不可能 考点: 可能性的大小. 分析: 可能性表示的是事情出现的概率,所求情况数占总情况数的比例越大,它出现的可 能性就越大. 解答: 解:从图中可以看出把整个圆平均分成了 8 份,阴影部分占了 7 份,而空白部分只 占了 1 份,阴影部分有,但不是全部,所以不能用一定和不可能来描述,阴影部分的可能性 大,就用很可能来描述. 故选:B. 点评: 本题主要考查了可能性大小的计算,可能性等于所求情况数与总情况数之比. 21.《快乐大本营》童装店以 100 元卖出两套不同的童装,结果一套赚 20%,一套亏本 20%,总的来说,这个童装店是( ) A. 亏本 B. 赚钱 C. 不亏也不赚 考点: 百分数的实际应用. 专题: 压轴题. 分析: 本题有两个不同的单位“1”,分别求解出这两套衣服的进价,再求出赚了和亏了多少 钱,进行比较. (1)赚了 20%,把这套衣服的进价看成单位“1”,那么 100 元就是单位“1”的 1+20%,用除 法就可以求出进价,进而求出赚了多少钱. (2)亏本 20%,这一套衣服的进价是单位“1”,那么 100 元就是单位“1”的 1﹣20%,用除法 就可以求出进价,进而求出亏了多少钱. 解答: 解:第一套衣服: 100÷(1+20%) =100÷120% ≈83.33(元); 100﹣83.33=16.67(元) 第二套衣服: 100÷(1﹣20%) =100÷80% =125(元); 125﹣100=25(元); 16.67<25,所以这个童装店亏了. 故选:A. 点评: 解答此题的关键是找单位“1”,进一步发现比单位“1”多或少百分之几,由此解决问 题. 四、看清题目,巧思妙算:(共 22 分) 22.(4 分)直接写出得数. 14÷35= 125+175= 0.77+0.33= 45×4+4×55= 4.36×0= 考点: 运算定律与简便运算;整数的加法和减法;小数乘法;小数除法. 专题: 运算顺序及法则. 分析: 本题题根据整数、小数的加法、减法、乘法、除法运算法则计算即可, 45×4+4×55 可以运用乘法分配律进行简算. 解答: 解:14÷35= 125+175=300 0.77+0.33=1.1 45×4+4×55=400 4.36×0=0 点评: 完成本题要注意分析式中数据,能简算的要简算. 23.(12 分)(2010•邢台)用递等式计算下面各题: (1)(0.125×8﹣0.5)×4 (2) ÷6+ × (3) ×0.25+ × (4)4﹣[3.75×(1.2﹣ )+ ]. 考点: 整数、分数、小数、百分数四则混合运算. 专题: 压轴题. 分析: 算式(1)可根据四则混合运算的运算顺序计算即可:先算乘除,再算加减,有括号 的要先算括号里面的; 算式(2)(3)可根据乘法分配律计算; 算式(4)可将括号中的乘法算式根据乘法分配律进行计算. 解答: 解:(1)(0.125×8﹣0.5)×4, =(1﹣0.5)×4, =0.5×4, =2; (2) ÷6+ × = × + × , =( + )× , = × , = ; (3) ×0.25+ × = × + × , =( + )× , =1× , = ; (4)4﹣[3.75×(1.2﹣ )+ ] =4﹣[3.75×( ﹣ )+ ], =4﹣[3.75× ﹣3.75× +0.75], =4﹣[4.5﹣1.25+0.75], =4﹣4, =0. 点评: 当算式中同时含有分数与小数时,可根据式中数据的特点,灵活将它们进行互化, 然后再计算. 五、实践操作,探索创新:(共 6 分) 25.(1)请你在如图正方形中画一个最大的圆. (2)如果该正方形的面积是 20 平方厘米,计算正方形的面积与圆面积的比. 考点: 画圆;比的意义;长方形、正方形的面积;圆、圆环的面积. 分析: (1)正方形内最大的圆就是以这个正方形的边长为直径的圆,由此以正方形的中心 为圆心,以正方形的边长的一半为半径即可画圆; (2)设圆的半径为 r,则正方形的边长就是 2r,根据正方形和圆的面积公式即可解答. 解答: 解:(1)以正方形的中心为圆心,以正方形的边长的一半为半径即可画圆,如图所 示; (2)设圆的半径为 r,则正方形的边长就是 2r,因为正方形的面积是 20 平方厘米, 所以 2r×2r=20, 4r2=20, r2=5, 所以圆的面积为:3.14×5=15.7(平方厘米), 所以正方形与圆的面积之比是:20:15.7=200:157; 答:正方形与圆的面积之比是 200:157. 点评: (1)圆的两大要素是:圆心和半径,由此即可画圆; (2)此题考查了圆的面积公式的灵活应用,此题关键是求出 r2=5,代入圆的面积公式计 算. 26.下面是六年级一班学生喜欢的电视节目统计图. (1)喜欢《走进科学》的同学人数占全班人数的 38 %. (2)喜欢《焦点访谈》的人数相当于喜欢《大风车》人数的 60 %,如果全班有 60 人, 那么,喜欢《大风车》的有 15 人. 考点: 扇形统计图;百分数的加减乘除运算;统计图表的综合分析、解释和应用. 专题: 压轴题. 分析: 根据统计图分析可知,绘制扇形统计图时是把全班人数看做单位“1”,根据比的意义 可以求得喜欢《焦点访谈》的人数相当于喜欢《大风车》人数的百分比,由此即可解决问 题. 解答: 解:根据扇形统计图分析可得: ①1﹣15%﹣25%﹣22%=38%; ②15%÷25%=60%, 60×25%=15(人); 答:①喜欢《走进科学》的同学人数占全班人数的 38%, ②喜欢《焦点访谈》的人数相当于喜欢《大风车》人数的 60%,如果全班有 60 人,那么, 喜欢《大风车》的有 15 人. 故答案为:38;60;15. 点评: 此题考查了扇形统计图的综合分析能力以及比的意义在扇形统计图中的灵活应用. 六、走进生活,解决问题:(共 32 分)直接写出答案:(共 12 分,每题 3 分) 27.(3 分)北京奥运会开幕式门票的最高价是 5000 元,比闭幕式门票的最高价贵 23%.闭 幕式门票的最高价是 4065 元. 考点: 百分数的实际应用. 专题: 分数百分数应用题. 分析: 开幕式门票的最高价是 5000 元,比闭幕式门票的最高价贵 23%,即开幕式门票是 闭幕式的 1+23%,根据分数除法的意义可知,闭幕式门票的最高价是 5000÷(1+23%). 解答: 解:5000÷(1+23%) =5000÷1.23 ≈4065(元) 答:闭幕式门票的最高价是 4065 元. 故答案为:4065. 点评: 完成本题要注意单位“1”的确定,将闭幕式票价当作单位“1”. 28.我、爸爸、妈妈三人今年的平均年龄是 30 岁,已知爸爸和妈妈两人的平均年龄是 39 岁, 你猜我今年是多少岁? 考点: 平均数的含义及求平均数的方法;年龄问题. 专题: 平均数问题. 分析: 根据“爸爸和妈妈两人的平均年龄是 39 岁”,知道爸爸和妈妈两人的年龄和是 (39×2),再根据“我、爸爸、妈妈三人的平均年龄正好是 30 岁,”知道我、爸爸、妈妈三人 的年龄和是(30×3),由此即可求出我的年龄. 解答: 解:30×3﹣39×2, =90﹣78, =12(岁); 答:我今年 12 岁. 故答案为:12. 点评: 解答此题的关键是根据平均数的意义,找出我、爸爸、妈妈三人的年龄和及爸爸和 妈妈两人年龄和,用三人的年龄和减去两人的年龄和就是要求的答案. 29.学校组织“红十字会”捐款活动,六年级学生共捐款 650 元,比五年级学生捐款数的 2 倍 少 150 元.五年级学生捐款 400 元. 考点: 列方程解应用题(两步需要逆思考). 专题: 列方程解应用题. 分析: 根据六年级学生的捐款比五年级学生捐款数的 2 倍少 150,可知本题的等量关系: 五年级学生捐款数×2﹣150=六年级学生捐款数,据此等量关系式可列方程解答. 解答: 解:设五年级学生捐款 x 元,根据题意得: 2x﹣150=650, 2x﹣150+150=650+150, 2x÷2=800÷2, x=400; 答:五年级学生捐款 400 元. 故答案为:400. 点评: 本题的关键是找出题目中的等量关系式,然后根据等量关系式列方程解答. 30.(3 分)小东计划把自己积蓄的 3000 元钱存入银行,存期一年,准备到期后把税后利息 (利息税按 20%计算)捐献给贫困地区的“特困生”,如果年利率按 2.25%计算,到期后他可 以捐出 54 元. 考点: 存款利息与纳税相关问题. 专题: 分数百分数应用题. 分析: 解答本题时,把利息看做单位“1”,税后利息是 1﹣20%,此题应根据关系式“利息= 本金×利率×时间×(1﹣20%)”列式解答即可. 解答: 解:3000×2.25%×1×(1﹣20%) =3000×0.0225×0.8×1 =54(元) 答:到期后他可以捐出 54 元. 故答案为:54. 点评: 此题考查学生对关系式“利息=本金×利率×时间”掌握与运用情况,在列式时,不要忘 记扣除利息税. 二、应用题.(共 18 分,每题 6 分) 31.张师傅加工一批零件,第一天完成的个数与零件的总个数的比是 1:3.如果再加工 15 个,就可以完成这批零件的一半.这批零件共有多少个? 考点: 简单的归一应用题;按比例分配应用题. 专题: 压轴题. 分析: 第一天完成的个数与零件的总个数的比是 1:3,那么第一天就完成了总数的 ,我 们设这批零件一共有 X 个,第一天就完成了 ,再加上 15 个就是一半 X 个.根据这个 等量关系列出方程. 解答: 解:设这批零件共 X 个. X﹣ X=15 X=15×6 X=90 答:这批零件共有 90 个. 点评: 本题还可以这样做:15 对应的分数是 ﹣ ,求单位“1”用除法,即 15÷( ﹣ ). 32.星期天,小华请 8 名同学到家作客,他妈妈用一盒长方体包装的饮料招待同学.这个长 方体盒子长 15 厘米,宽 12 厘米,高 20 厘米,给每个同学倒了一满杯,杯子的底面积是 50.24 平方厘米,高是 8 厘米,招待客人后,小华他自己还有饮料喝吗?(写出计算过程) 考点: 长方体、正方体表面积与体积计算的应用. 专题: 压轴题. 分析: 此题可先求出饮料的体积,再求出 8 个杯子的体积,两个结果进行比较,即可得出 答案. 解答: 解:15×12×20=3600(立方厘米), 50.24×8×8=3215.36(立方厘米), 3600>3215.36, 答:他自己还有饮料喝. 点评: 此题主要考查长方体的体积计算公式,只要饮料的体积多于 8 个杯子的体积,小华 就还有饮料喝. [来源:学科网 ZXXK] 33.武汉移动通信公司推出两种手机卡,采用的收费标准见下表: 种类 固定月租费 每分通话费 A 卡 16 元 0.12 元 B 卡 0 元 0.3 元 妈妈每月的通话时间累计一般在 60 分左右,爸爸每月的通话时间累计一般在 200 分左右, 请你帮助他们分别选一种比较合算的手机卡,并通过计算说明你的理由. 考点: 最优化问题. 专题: 压轴题. 分析: 由图表中的收费标准可知,A 卡有固定月租费,每分钟收费比较便宜;B 卡没有月 租费,但每分钟的收费比较高.由此可知,当通话时间小于一定值时,选用 B 卡比较便宜, 当通话时间大于这个值时,采用 A 卡比较便宜;由此可设这个值为 x,可行方程: 16+0.12x=0.3x,解此方程,得出这个时间值后,即能确定他们分别选一种比较合算. 解答: 解:设当通话时间低于 x 分钟时,选用 B 卡比较便宜,当通话时间大于 x 分钟时, 采用 A 卡比较便宜, 由此可得: 16+0.12x=0.3x[来源:学科网 ZXXK] 0.18x=16, x≈89. 答:当通话时间低于 89 分钟时,选用 B 卡比较便宜,当通话时间大于 89 分钟时,采用 A 卡比较便宜. 60 分钟<89 分钟,200 分钟>89 分钟, 所以,妈妈应选用 B 卡,爸爸应选用 A 卡比较便宜. 点评: 本题也可根据妈妈与爸爸每月的通话时间及此费标准分别计算分析,得出结论.查看更多