中考数学 平行四边形复习

中考数学 平行四边形复习

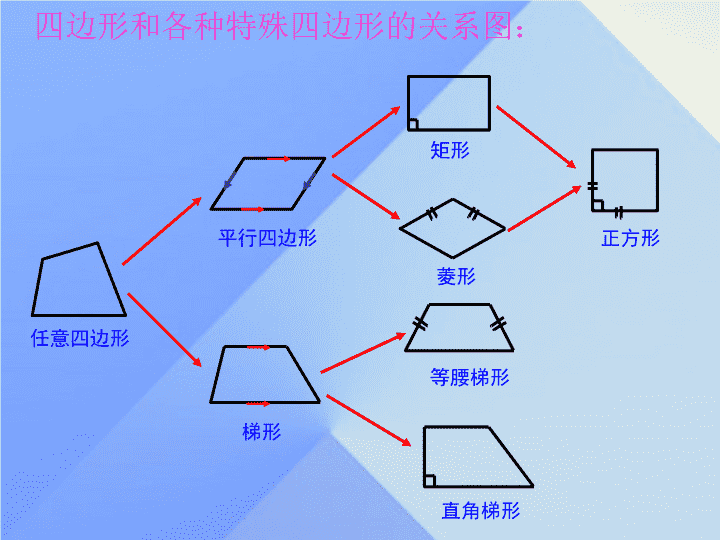
中考复习 平行四边形 梯形 平行四边形 任意四边形 四边形和各种特殊四边形的关系图： 菱形 矩形 等腰梯形 直角梯形 正方形 用集合的观点来表示四边形的分类 四边形 平行四边形 菱形 矩形 正方形 梯形 等腰梯形 直角梯形 梯形 平行四边形 任意四边形 四边形和各种特殊四边形的关系图： 菱形 矩形 等腰梯形 直角梯形 正方形 知识回顾 A B C D O (2) 两组对角分别相等，邻角互补。 (1) 两组对边分别平行且相等。 (4) 平行四边形是中心对称图形。 (3) 对角线互相平分。 1 、定义 : 两组对边分别平行的四边形叫做 平行四边形。 2 、平行四边形的性质 ∥ ＝ ∥ ＝ CD ， AB BC AD □ ABCD AO=CO ， BO=DO □ ABCD □ ABCD A B C D 如图，四边形 ABCD 是平行四边形吗？ (1) 两 组 对边 分别平行的四边形是 平行四边形 。 (2) 一 组 对边 平行且相等的四边形是 平行四边形 。 ∵AB∥DC ， AD∥BC ∴ 四边形 ABCD 是平行四边形 ∵AB∥DC ， AB ＝ DC ∴ 四边形 ABCD 是平行四边形 ∵AD∥BC ， AD ＝ BC ∴ 四边形 ABCD 是平行四边形 或 3 、平行四边形的判定 (3) 两组 对边 分别相等的四边形是 平行四边形 。 ∵AB=DC ， AD=BC ∴ 四边形 ABCD 是平行四边形 (4) 两组 对角 分别相等的四边形是 平行四边形 。 ∵∠A=∠C ,∠B=∠D ∴ 四边形 ABCD 是平行四边形 (5) 对角线 互相平分的四边形是 平行四边形 。 ∵AO=CO ， BO=DO ∴ 四边形 ABCD 是平行四边形 A B C D O 基础训练 1 、若 □ ABCD 的周长为 24cm ，其中 AB=5cm ， 则 BC=___cm ， AD=___cm ， CD=___cm. 2 、 □ ABCD 中 ,∠A+∠C=200 °, 则∠ A=____° ， ∠D=____°. 3 、已知 □ ABCD 中， AC=10cm, BD=16cm, 则 BC 的取值范围 是 _______________________ 。 7 7 5 A B C D 4 、在△ ABC 中 , AB=AC=6cm, D 是 BC 上一点，且 DE∥AC ， 交 AB 于 E, DF∥AB, 交 AC 于 F, 则四边形 AEDF 的周长为 ( 　　 ). B (A)6cm (B)12cm (C)18cm (D)24cm A B C D E F 5 、如图所示，在 □ ABCD 中， DB ＝ DC ， ∠ C ＝ 70°, AE⊥BD 于 E, 则∠ DAE 等于 ( ). (A) 20° (B) 25° (C) 30° (D) 35° A 6 、如图 , □ ABCD 的对角线 AC ， BD 交于 O, EF 过点 O ， 与 AD ， BC 分别交于 E ， F ，如果 AB=4 ， BC=5 ， OE=1.5 ， 则四边形 EFCD 的周长是 ( ). (A)16 (B)14 (C)12 (D)10 A B C D E F O C 3cm A B D C 5cm 4cm 1 、如图，在 □ ABCD 中，已知 BC=5cm, DC=3cm, AC=4cm. 求 □ ABCD 的面积 . 共同提高 解： 2 、已知 : 如图 , 在 □ ABCD 中 ,E ， F 分别是 AB ， DC 上的两点 , 且 DF=EB. 求证 :DE=BF . A B E F D C 证明 :∵ 四边形 ABCD 是平行四边形 ∴DC∥AB 又 ∵ DF=EB ∴ 四边形 DEBF 是平行四边形 ( 一组对边平行且相等的 四边形是平行四边形 ) ∴ DE=BF 3 、如图 , 平行四边形 ABCD 的对角线 AC ， BD 交于点 O, E ， F 是 AC 上的两点 , 并且 AE=CF. 求证 : 四边形 BFDE 是平行四边形 . 证明∵四边形 ABCD 是平行四边形 ∴AO=CO , BO=DO ∵AE=CF ∴EO=FO 又∵ BO=DO ∴ 四边形 BFDE 是平行四边形 . A B C O E F D A B D C O F E 思维拓展 1 、如图所示，在 □ ABCD 中，点 E ， F 在对角线 AC 上，且 AE ＝ CF. 请你以 F 为一个端点，和图中已标明字母的某一点连成一条新线段，猜想并说明它和图中已有的某一条线段相等 ( 只须说明一组线段相等即可 ). （ 1 ）连结 ____________ ； （ 2 ）猜想： ____________ ＝ ____________ ； （ 3 ）说明所猜想的结论的正确性 . D C A B E F 2 、 □ ABCD 的周长为 32cm, ∠ABC 的角平分线交边 AD 所在直线于点 E ，且 AE ： ED=3 ： 2 ，求 AB 的长． A B C D E A B C D E 3 、 有一等腰三角形的木格子，里面的每一木条同方向都平行，已知等腰三角形的腰长是 30cm ，底边长是 50cm ，你能帮木工师傅算出拼木格子所需木条的总长度吗？ 总长度 =30+30+50+30×1 总长度 =30+30+50+30×2 总长度 =30+30+50+30×3 总长度 =30+30+50+30×4 总长度 =30+30+50+30×? 从以上的操作你能发现什么规律吗？ 3 、 有一等腰三角形的木格子，里面的每一木条同方向都平行，已知等腰三角形的腰长是 30cm ，底边长是 50cm ，你能帮木工师傅算出拼木格子所需木条的总长度吗？ 4 、已知四边形 ABCD 的 对角线相交于点 O ，从 ① AB∥CD ②AB=CD ③AD∥BC ④AD=BC ⑤∠ABC=∠ADC ⑥AO=CO 中任取两个条件加以组合， 能推出四边形 ABCD 是 平行四边形的概率是多少？ A B C D O ①② ①③ ①④ ①⑤ ①⑥ ②③ ②④ ②⑤ ②⑥ ③④ ③⑤ ③⑥ ④⑤ ④⑥ ⑤⑥ √ √ × √ √ × √ × × √ √ √ × × × ∴ 能推出四边形 ABCD 是平行四边形的概率 = 课堂小结 一、知识要点 1 、平行四边形的定义 : 两组对边分别平行的四边形叫做平行四边形 2 、平行四边形的性质 : (1) 对边平行且相等 (2) 对角相等，邻角互补 (3) 对角线互相平分 3 、平行四边形的判定 : (1) 两组对边分别平行的四边形叫做平行四边形 (2) 两组对边分别相等的四边形是平行四边形 (3) 一组对边平行且相等的四边形是平行四边形 (4) 两组对角分别相等的四边形是平行四边形 (5) 对角线互相平分的四边表是平行四边形 二、学习方法 1 、平行四边形是特殊的四边形，其特殊性体现在“平行”上，由定义 可知，平行四边形的两组对边分别平行，既可作为性质，也可以作 为平行四边形的判定使用。 2 、就定理的条件与结论而言，平行四边形的性质与判定的条件与 结论正好相反，在学习中明确，性质是以平行四边形为出发点，而 判定则是以平行四边形为定向目标，使用时切不可张冠李戴。 3 、在探索平行四边形的性质时 , 可以用平移、翻折、旋转等观点进行探索。 谢谢大家！