- 2021-04-12 发布 |
- 37.5 KB |
- 9页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2014年湖南省常德市中考数学试题(含答案)
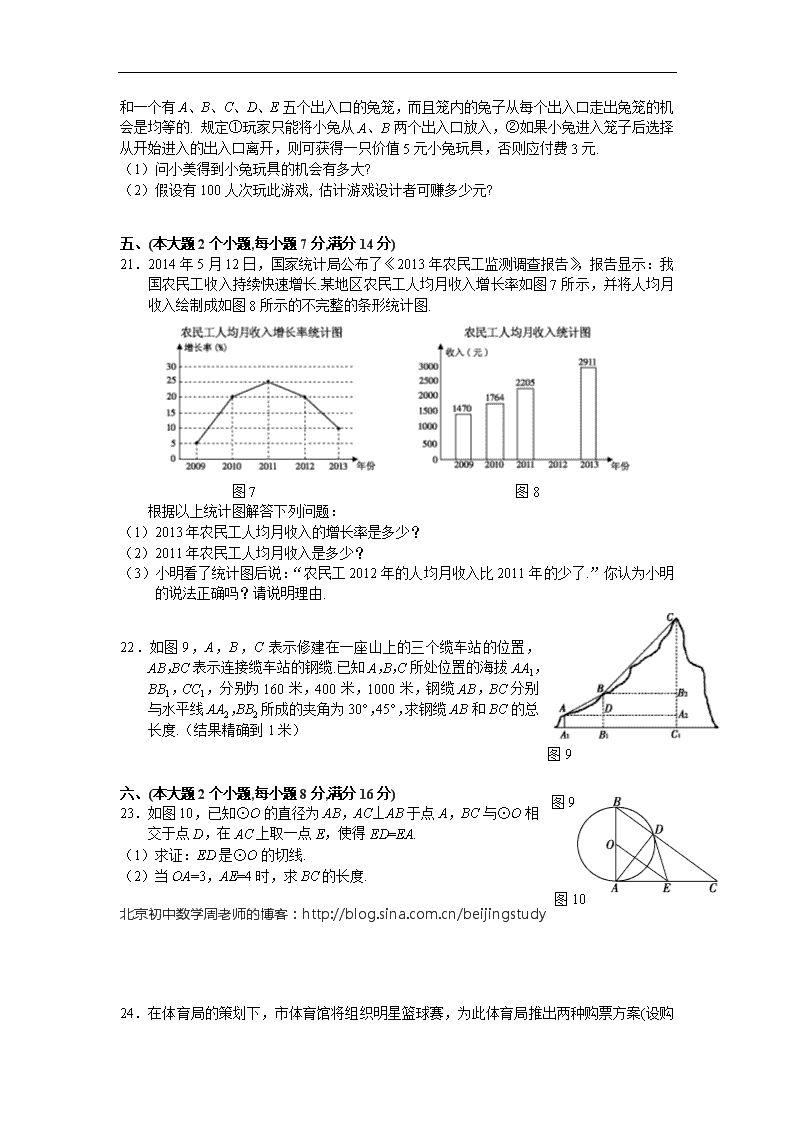
2014年常德市初中毕业学业考试数学试题 考生注意:1、请考生在试题卷首填写好准考证号及姓名. 2、请将答案填写在答题卡上,填写在试题卷上的无效. 3、本学科试题卷共 4页,七道大题,满分120 分,考试时量 120 分钟. 4、考生可带科学计算器参加考试. 一、选择题(本大题8个小题,每小题3分,满分24分) 1.等于 A.2 B. C. D. 图1 A. B. C. D. 2.如图1所示的几何体的主视图是 3.下列各数:,其中无理数的个数是 A.1个 B.2个 C.3个 D.4个 4.下列各式与是同类二次根式的是 图2 A. B. C. D. 5.如图2,已知AC∥BD,∠CAE=30°, ∠DBE=45,则∠AEB等于 A.30° B.45° C.60° D.75° 6.某班体育委员记录了7位女生1分钟仰卧起坐的个数分别为28,38,38,35,35,38,48,这组数据的中位数和众数分别是 A.35,38 B.38,35 C.38,38 D.35,35 7.下面分解因式正确的是 A. B. C. D. 8.阅读理解:如图3,在平面内选一定点,引一条有方向的射线,再选定一个单位长度,那么平面上任一点M的位置可由的度数与的长度m确定,有序数对(,m)称为点的“极坐标”,这样建立的坐标系称为“极坐标系”. 应用:在图4的极坐标系下,如果正六边形的边长为2,有一边OA在射线上,则正六边形的顶点C的极坐标应记为 A.(60°,4) B.(45°,4) C.(60°,2) D.(50°,2) [来源:学.科.网Z.X.X.K] 图3 图4 二、填空题(本大题8个小题,每小题3分,满分24分) 9.要使式子在实数范围内有意义,则的取值范围是________________. 10.古生物学家发现350 000 000年前,地球上每年大约是400天,用科学记数法表示350 000 000=_______________. 11.下列关于反比例函数的三个结论:①它的图象经过点(7,3);②它的图象在每一个象限内,随的增大而减小;③它的图象在二、四象限内.其中正确的是________________. 12.计算:=___________. 图5 13.一元二次方程有两个不相等的实数根, 则的取值范围是________________. 14.如图5所示,AB为⊙O的直径,CD⊥AB,若AB=10, CD=8,则圆心O到弦CD的距离为_________. 15.如图6,已知△ABC三个内角的平分线交于点O,点D在CA的延长线上,且DC=BC,AD=AO, 若∠BAC=,则∠BCA的度数为 . 图6 16.已知: 计算: ; 猜想: . 三、 (本大题2个小题,每小题5分,满分10分) 17.计算: 18.解方程: 四、(本大题2个小题,每小题6分,满分12分) 19.解不等式组 北京初中数学周老师的博客:http://blog.sina.com.cn/beijingstudy 20.小美周末来到公园,发现在公园一角有一种 “守株待兔”游戏.游戏设计者提供了一只兔子和一个有A、B、C、D、E五个出入口的兔笼,而且笼内的兔子从每个出入口走出兔笼的机会是均等的. 规定①玩家只能将小兔从A、B两个出入口放入,②如果小兔进入笼子后选择从开始进入的出入口离开,则可获得一只价值5元小兔玩具,否则应付费3元. (1)问小美得到小兔玩具的机会有多大? (2)假设有100人次玩此游戏, 估计游戏设计者可赚多少元? 五、(本大题2个小题,每小题7分,满分14分) 21.2014年5月12日,国家统计局公布了《2013年农民工监测调查报告》,报告显示:我国农民工收入持续快速增长.某地区农民工人均月收入增长率如图7所示,并将人均月收入绘制成如图8所示的不完整的条形统计图. 图7 图8 根据以上统计图解答下列问题: (1)2013年农民工人均月收入的增长率是多少? (2)2011年农民工人均月收入是多少? (3)小明看了统计图后说:“农民工2012年的人均月收入比2011年的少了.”你认为小明的说法正确吗?请说明理由. 图9 22.如图9,A,B,C表示修建在一座山上的三个缆车站的位置,AB,BC表示连接缆车站的钢缆.已知A,B,C所处位置的海拔AA1,BB1,CC1,分别为160米,400米,1000米,钢缆AB,BC分别与水平线AA2,BB2所成的夹角为30°,45°,求钢缆AB和BC的总长度.(结果精确到1米) 图9 六、(本大题2个小题,每小题8分,满分16分) 23.如图10,已知⊙O的直径为AB,AC⊥AB于点A,BC与⊙O相交于点D,在AC上取一点E,使得ED=EA. (1)求证:ED是⊙O的切线. (2)当OA=3,AE=4时,求BC的长度. 图10 北京初中数学周老师的博客:http://blog.sina.com.cn/beijingstudy 24.在体育局的策划下,市体育馆将组织明星篮球赛,为此体育局推出两种购票方案( 设购票张数为,购票总价为): 方案一: 提供8 000元赞助后,每张票的票价为50元; 方案二: 票价按图11中的折线OAB所表示的函数 关系确定. (1)若购买120张票时, 按方案一和方案二分别应付的购票款是多少? (2)求方案二中与的函数关系式; 图11 (3)至少买多少张票时选择方案一比较合算? 七、(本大题2个小题,每小题10分,满分20分) 25.如图12, 已知二次函数的图像过点O(0,0), A(4,0),B(),M是OA的中点. (1)求此二次函数的解析式; (2)设P是抛物线上的一点,过P作轴的平行线与抛物线交于另一点Q,要使四边形PQAM是菱形,求P点的坐标; 图12 (3)将抛物线在轴下方的部分沿轴向上翻折,得曲线OB′A(B′为B关于轴的对称点),在原抛物线轴的上方部分取一点C,连接CM,CM与翻折后的曲线OB′A交于点D,若△CDA的面积是△MDA面积的2倍,这样的点C是否存在?若存在求出C点的坐标,若不存在,请说明理由. 26.如图13,14,已知四边形ABCD为正方形,在射线AC上有一动点P,作PE⊥AD(或延长线)于E,作PF⊥DC(或延长线)于F,作射线BP交EF于G. (1)在图13中,设正方形ABCD的边长为2, 四边形ABFE的面积为y, AP=,求y关于的函数表达式. (2)结论GB⊥EF对图13,图14都是成立的,请任选一图形给出证明; (3)请根据图14证明:△FGC∽△PFB. 图13 图14 2014年常德市初中毕业学业考试 数学参考答案及评分标准 说明: (一)《答案》中各行右端所注分数表示正确作完该步应得的累加分数,全卷满分120分. (二)《答案》中的解法只是该题解法中的一种或几种,如果考生的解法和本《答案》不同,可参照本答案中的标准给分。 (三)评卷时要坚持每题评阅到底,勿因考生解答中出现错误而中断本题的评阅。如果考生的解答在某一步出现错误,影响后继部分而未改变本题的内容和难度者,视影响程度决定后面部分的得分,但原则上不超过后面部分应得分数的一半,如有严重的概念错误,就不给分。 一、选择题(本大题8个小题,每小题3分,满分24分) 1.A 2.B 3.B 4.D 5.D 6.C 7.C 8.A 二、填空题(本大题8个小题,每小题3分,满分24分) 9. 10.3.5×108 11.①② 12. 13. 14.3 15.60° 16., 注:16题对一空记2分,对二空记3分. 三、 (本大题2个小题,每小题5分,满分10分) 17.解:原式=4+14 …………………………………………4分 = …………………………………………5分 注:第一个等号每算对一个运算给1分,共4分 18.解:方程两边同乘以,得 ……………………………2分 ……………………………4分 经检验:是原方程的根 所以原方程的解是. ……………………………5分 四、 (本大题2个小题,每小题6分,满分12分) 19.解:解不等式①,得 ……………………………2分[来源:学。科。网] 解不等式②,得 ……………………………4分 所以不等式组的解集是 ……………………………6分 开始 入口 A B 出口 A B C D E A B C D E 20.解:(1)画树状图(或列表略) ……………………………2分 小美得到小兔玩具的概率= ……………………………4分 (2)100人次玩此游戏,估计有人次会获得玩具,花费20×5=100元, 估计将有100-20=80人次要付费, 估计游戏设计者可赚80×3-100=140(元). ……………………………6分 五、 (本大题2个小题,每小题7分,满分14分) 21.解:(1)10% ……………………………2分 (2)2205元 ……………………………4分 (3)不正确 ……………………………5分 2012的人均月收入= …………7分 22.解:在Rt△ABD中, BD=400-160=240, ∠BAD=30° ……………………………1分 则AB=2BD=480 m. ……………………………3分 在Rt△BCB2中, CB2=1000-400=600,∠CBB2=45° ……………………………4分 则CB=600m. ……………………………6分 所以AB+BC=480+600 ≈1328 (米) 答:钢缆AB和BC的总长度约为1328米. ……………………………7分 A B C E D O 1 2 3 4 5 6 六、 (本大题2个小题,每小题8分,满分16分) 23.解:(1)证明:连结OD. ∵OD=OA,EA=ED, ∴∠3=∠4, ∠1=∠2 ……………2分 ∴∠1+∠3=∠2+∠4 , 即∠ODE=∠OAE ∵AB⊥AC, ∠OAE=90° ∴∠ODE=90°∴DE是⊙O的切线. ………4分[来源:Z_xx_k.Com] (2)∵OA=3, AE=4 ∴OE=5 ………5分 图10 又∵AB是直径, ∴AD⊥BC ∴∠1+∠5=90°,∠2+∠6=90° 又∵∠1=∠2 ∴∠5=∠6 ,∴DE=EC, ……………………………6分 ∴E是AC的中点. ∴OE∥BC且 OE=BC ∴BC=10 ……………………………8分 24.解:(1)按方案一购120张票时,(元); 按方案二购120张票时,由图知(元)……………………2分 (2)当时,设,则, ∴. ……………………………3分[来源:学|科|网] 时, 设, 解得, ∴ 综合上面所得 …………………………5分 (3)由(1)知, 购120张票时,按方案一购票不合算. 即选择方案一比较合算时,应超过120. …………………………6分 设至少购买张票时选择方案一比较合算 则应有, 解得:(张) ∴至少买200张时选方案一. …………………………8分 七、 (本大题2个小题,每小题10分,满分20分) O A M P Q C D B/ B D1 C1 图12 25.解: (1)方法一:设二次函数的解析式为 则 ∴ ……3分 方法二:∵图像过点O(0,0), A(4,0), ∴设, 又B()在曲线上,∴,∴ ∴ ……………………………………3分 (2)∵M是OA的中点,OA=4,∴MA=2, 若四边形PQAM是菱形,则PQ=2, 又根据抛物线关于对称轴对称,即P、Q关于直线对称, ∴P的横坐标为1, Q的横坐标为3. ……………………………………5分 ∴P的坐标为(1,, Q的横坐标为(3,. 而计算PM=,故所求的P(1,满足四边形PQAM是菱形 ………6分 (3)设存在这样的C点.设C、D的坐标分别为[来源:学科网ZXXK] ∵二次函数在轴下方的部分向上翻折,得曲线OB′A, ∴曲线OB′A的解析式为……………………………………7分 若△CDA的面积是△MDA面积的2倍, ∴△CMA的面积是△MDA面积的3倍, ∴, ∴,即, ∴……………① …………………………8分 过D,C分别作DD1,CC1垂直于轴, ∴△MD1D∽△MC1C, ∴,∴ 即………………② …………………………9分 将②代入①得: ,代入二次函数的解析式得 故C的坐标为,或. ………………………10分 26.解:(1)∵EPAD,PFDC,∴四边形EPFD是矩形, ∵AP=, ∴AE=EP=DF=, , …………………………1分 ∴ A B C E P F G D 答案图13-1 H ………………………………3分 (2)在图13中证明GB⊥EF. ①证法一:延长FP交AB于H, ∵PF⊥DC,PE⊥AD,∴PF⊥PE,PH⊥HB, 即∠BHP=90° ………………………………4分 ∴在Rt△FPE与Rt△BHP中 因 ABCD是正方形, ∴易知PF=FC=HB,EP=PH ∴Rt△FPE≌Rt△BHP……………………………5分 ∴∠PFE=∠PBH, 又∠FPG=∠BPH, ∴△FPG∽ △BPH, ∴∠FGP=∠BHP=90°,即GB⊥EF ………………………………6分 分析: 要GB⊥EF,只要∠5 +∠3=90°,而∠5 +∠4=90°,只要证∠3=∠4, 而∠2 =∠3, ,只要证∠4=∠2,而∠4=∠1,故只要∠1=∠2. 证法二: 如答案图13-2,连接PD,延长FP交AB于H, 延长EP交BC于M, 易知DC=BC, ∠DCP=∠BCP=45°,PC=PC, C F D A B E P G 答案图13-2 H M 3 2 4 1 5 A. B. C. D. ∴△DPC≌△BPC……………………4分 ∴∠DPC=∠BPC,即∠1+45°=45°+∠2, ∴∠1=∠2,……………………………5分 而∠1=∠4, ∠2 =∠3, ∴∠3=∠4, 而∠5 +∠4=90°,∴∠5 +∠3=90°, ∴∠PGE=180°-(∠5 +∠3)=90°, 即GB⊥EF.……………………………6分 注:在图14中证法与上面类似. (3)证法一: ∵GB⊥EF,∴…①……7分 连接PD,在△DPC和△BPC中 ∵DC=BC, ∠DCP=∠BCP=135°,PC=PC, ∴ △DPC≌△BPC,∴PD=PB. ………………………8分 而PD=EF, ∴EF=PB. 又∵GB⊥EF,∴ ∴ 而PF=FC, ∴ ………………………9分 ∴………② ∴由①②得△FGC∽△PFB. ………………………10分 证法二: ∵GB⊥EF,∴………① ………………………7分 又∵ 取BF的中点M,则有: ∴B,C,G,F四点在以M为圆心,MB为半径的圆上. …………………………9分 ∴………② ∴由①②得△FGC∽△PFB. …………………………10分 3查看更多