- 2021-04-12 发布 |
- 37.5 KB |
- 14页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2016挑战中考数学压轴题图形的平移翻折与旋转
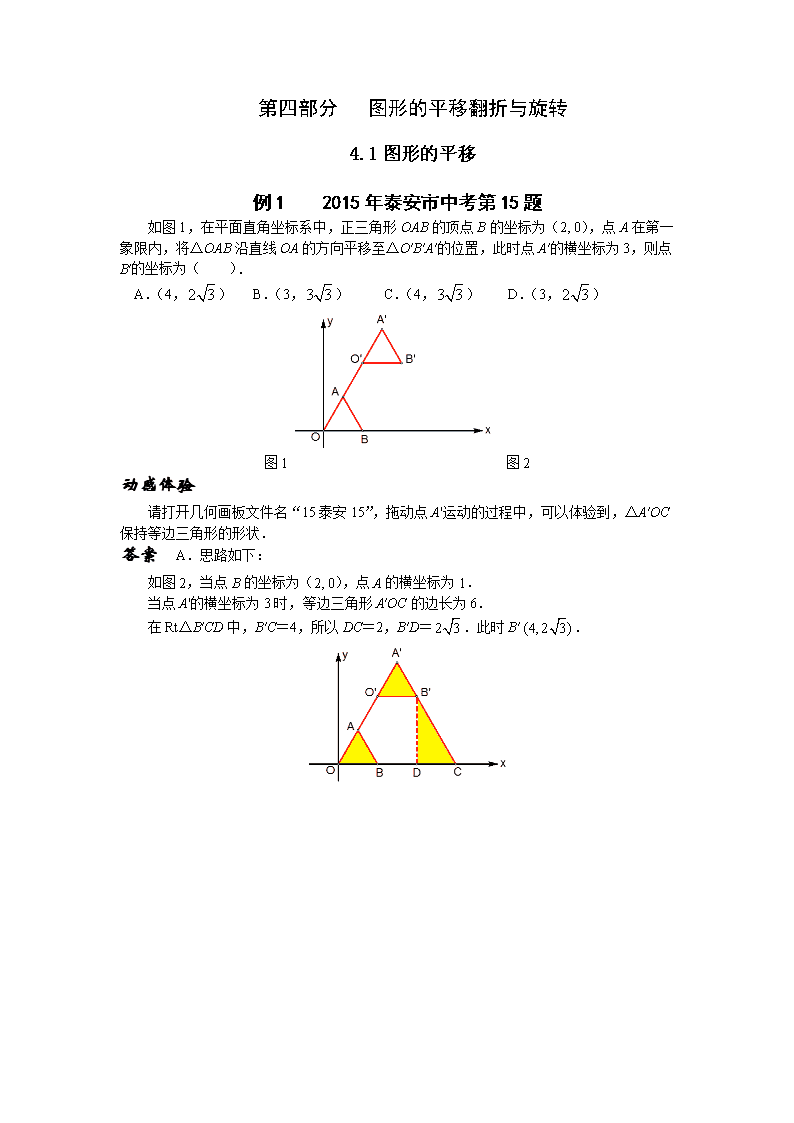
第四部分 图形的平移翻折与旋转 4.1图形的平移 例1 2015年泰安市中考第15题 如图1,在平面直角坐标系中,正三角形OAB的顶点B的坐标为(2, 0),点A在第一象限内,将△OAB沿直线OA的方向平移至△O′B′A′的位置,此时点A′的横坐标为3,则点B′的坐标为( ). A.(4,) B.(3,) C.(4,) D.(3,) 图1 图2 动感体验 请打开几何画板文件名“15泰安15”,拖动点A'运动的过程中,可以体验到,△A′OC保持等边三角形的形状. 答案 A.思路如下: 如图2,当点B的坐标为(2, 0),点A的横坐标为1. 当点A'的横坐标为3时,等边三角形A′OC的边长为6. 在Rt△B′CD中,B′C=4,所以DC=2,B′D=.此时B′. 例2 2014年江西省中考第11题 如图,在△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿射线BC方向平移2个单位后,得到△A′B′C′,联结A′C,则△A′B′C的周长为_______. 动感体验 请打开几何画板文件名“14江西11”,拖动点B′运动,可以体验到,△A′B′C′向右移动2个单位后,△A′B′C是等边三角形. 答案 12. 4.2图形的翻折 例1 2015年上海市宝山区嘉定区中考模拟第18题 如图1,在矩形ABCD中,AD=15,点E在边DC上,联结AE,△ADE沿直线AE翻折后点D落到点F,过点F作FG⊥AD,垂足为G.如果AD=3GD,那么DE=_____. 图1 动感体验 请打开几何画板文件名“15宝山嘉定18”,拖动点E在DC上运动,可以体验到, △ADE与△AFE保持全等,△AMF与△FNE保持相似(如图2所示). 答案 .思路如下: 如图2,过点F作AD的平行线交AB于M,交DC于N. 因为AD=15,当AD=3GD时,MF=AG=10,FN=GD=5. 在Rt△AMF中,AF=AD=15,MF=10,所以AM=. 设DE=m,那么NE=. 由△AMF∽△FNE,得,即.解得m=. 图2 例2 2014年上海市中考第18题 如图,已知在矩形ABCD中,点E在边BC上,BE=2CE,将矩形沿着过点E的直线翻折后,点C、D分别落在边BC下方的点C′、D′处,且点C′、D′、B在同一条直线上,折痕与边AD交于点F,D′F与BE交于点G.设AB=t,那么△EFG的周长为______________(用含t的代数式表示). 图1 动感体验 请打开几何画板文件名“14福州10”,拖动点F在AD上运动,可以体验到,当点C′、D′、B在同一条直线上时,直角三角形BCE的斜边BE等于直角边C′E的2倍,△BCE是30°角的直角三角形,此时△EFG是等边三角形(如图2). 答案 .思路如下:如图2,等边三角形EFG的高=AB=t,计算得边长为. 图2 4.3图形的旋转 例1 2015年扬州市中考第17题 如图1,已知Rt△ABC中,∠ABC=90°,AC=6,BC=4,将△ABC绕直角顶点C顺时针旋转90°得到△DEC,若点F是DE的中点,连接AF,则AF= . 图1 图2 动感体验 请打开几何画板文件名“15扬州17”,拖动点D绕着点C旋转,可以体验到,当旋转角为90°时,FH是△ECD的中位线,AF是直角三角形AHF的斜边. 答案 5.思路如下: 如图2,作FH⊥AC于H. 由于F是ED的中点,所以HF是△ECD的中位线,所以HF=3. 由于AE=AC-EC=6-4=2,EH=2,所以AH=4.所以AF=5. 例2 2014年上海市黄浦区中考模拟第18题 如图1,在△ABC中,AB=AC=5,BC=4,D为边AC上一点,且AD=3,如果△ABD绕点A逆时针旋转,使点B与点C重合,点D旋转至D',那么线段DD'的长为 . 图1 动感体验 请打开几何画板文件名“14黄浦18”,拖动点B'绕点A逆时针旋转,可以体验到,两个等腰三角形ABB'与等腰三角形ADD'保持相似(如图2). 答案 .思路如下:如图3,由△ABC∽△ADD',可得.5∶4=3∶DD'. 图2 图3 4.4三角形 例1 2015年上海市长宁区中考模拟第18题 如图1,△ABC≌△DEF(点A、B分别与点D、E对应),AB=AC=5,BC=6.△ABC固定不动,△DEF运动,并满足点E在BC边从B向C移动(点E不与B、C重合),DE始终经过点A,EF与AC边交于点M,当△AEM是等腰三角形时,BE=_________. 图1 动感体验 请打开几何画板文件名“15长宁18”,拖动点E在BC上运动,可以体验到,△AEM有三个时刻成为等腰三角形,其中一个时刻点E与点B重合. 答案 或1.思路如下: 设BE=x. 由△ABE∽△ECM,得,即. 等腰三角形AEM分三种情况讨论: ①如图2,如果AE=AM,那么△AEM∽△ABC. 所以.解得x=0,此时E、B重合,舍去. ②如图3,当EA=EM时,.解得x=1. ③如图4,当MA=ME时,△MEA∽△ABC.所以.解得x=. 图2 图3 图4 例2 2014年泰州市中考第16题 如图1,正方形ABCD的边长为3cm,E为CD边上一点,∠DAE=30°,M为AE的中点,过点M作直线分别与AD、BC相交于点P、Q.若PQ=AE,则AP的长等于__________cm. 图1 动感体验 请打开几何画板文件名“14泰州16”,拖动点P在AD上运动,观察度量值,可以体验到,存在两个时刻PQ=AE. 答案 1或2.思路如下:如图2,当PQ=AE时,可证PQ与AE互相垂直. 在Rt△ADE中,由∠DAE=30°,AD=3,可得AE=. 在Rt△APM中,由∠PAM=30°,AM=,可得AP=2. 在图3中,∠ADF=30°,当PQ=DF时,DP=2,所以AP=1. 图2 图3 4.5四边形 例1 2015年安徽省中考第9题 如图1,矩形ABCD中,AB=8,BC=4.点E在边AB上,点F在边CD上,点G、H在对角线AC上.若四边形EGFH是菱形,则AE的长是( ). A. B. C.5 D.6 图1 动感体验 请打开几何画板文件名“15安徽09”,拖动点E在AB上运动,可以体验到,当EF与AC垂直时,四边形EGFH是菱形(如图2). 答案 C.思路如下: 如图3,在Rt△ABC中,AB=8,BC=4,所以AC=. 由cos∠BAC=,得.所以AE=5. 图2 图3 例2 2014年广州市中考第8题 将四根长度相等的细木条首尾相接,用钉子钉成四边形ABCD,转动这个四边形,使它形状改变.当∠B=90°时,如图1,测得AC=2.当∠B=60°时,如图2,AC等于( ). (A); (B)2; (C) ; (D) 2. 图1 图2 动感体验 请打开几何画板文件名“14广州08”,拖动点A绕着点B旋转,可以体验到,当∠B=90°时,△ABC是等腰直角三角形;当∠B=60°时,△ABC是等边三角形(如图3). 答案 (A).思路如下: 4.6圆 例1 2015年兰州市中考第15题 如图1,⊙O的半径为2,AB,CD是互相垂直的两条直径,点P是⊙O上任意一点(P与A,B,C,D不重合),过点P作PM⊥AB于点M,PN⊥CD于点N,点Q是MN的中点,当点P沿着圆周转过45°时,点Q走过的路径长为__________. A. B. C. D. 图1 动感体验 请打开几何画板文件名“15兰州15”,拖动点P在圆周上运动一周,可以体验到,当点P沿着圆周转过45°时,点Q走过的路径是圆心角为45°半径为1的一段弧. 答案 A.思路如下: 如图2,四边形PMON是矩形,对角线MN与OP互相平分且相等,因此点Q是OP的中点. 如图3,当∠DOP=45°时,的长为. 图2 图3 例2 2014年温州市中考第16题 如图1,在矩形ABCD中,AD=8,E是AB边上一点,且AE=AB,⊙O经过点E,与边CD所在直线相切于点G(∠GEB为锐角),与边AB所在直线相交于另一点F,且EG∶EF=∶2.当边AD或BC所在的直线与⊙O相切时,AB的长是________. 图1 动感体验 请打开几何画板文件名“14温州16”,拖动点B运动,可以体验到,⊙O的大小是确定的,⊙O既可以与BC相切(如图3),也可以与AD相切(如图4). 答案 12或4.思路如下: 如图2,在Rt△GEH中,由GH=8,EG∶EF=∶2,可以得到EH=4. 在Rt△OEH中,设⊙O的半径为r,由勾股定理,得r2=42+(8-r)2.解得r=5. 设AE=x,那么AB=4x. 如图3,当⊙O与BC相切时,HB=r=5. 由AB=AE+EH+HB,得4x=x+4+5.解得x=3.此时AB=12. 如图4,当⊙O与AD相切时,HA=r=5. 由AE=AH-EH,得x=5-4=1.此时AB=4. 图2 图3 图4 4.7函数图像的性质 例1 2015年青岛市中考第8题 如图1,正比例函数的图像与反比例函数的图像相交于A、B两点,其中点A的横坐标为2,当y1>y2时,x的取值范围是( ). A.x<-2或x>2 B. x<-2或0<x<2 C.-2<x<0或0<x<2 D.-2<x<0或x>2 图1 动感体验 请打开几何画板文件名“15青岛08”,拖动点D在x轴上运动,观察线段EF的两个端点E、F的位置关系,可以体验到,当-2<x<0或x>2时,点E在点F的上方. 答案 D.如图2所示. 图2 例2 2014年苏州市中考第18题 如图1,直线l与半径为4的⊙O相切于点A,P是⊙O上一个动点(不与点A重合),过点P作PB⊥l,垂足为B,联结PA.设PA=x,PB=y,则(x-y)的最大值是_____. 图1 动感体验 请打开几何画板文件名“14苏州18”,拖动点P在圆上运动一周,可以体验到,AF的长可以表示x-y,点F的轨迹象两叶新树丫,当AF最大时,OF与AF垂直(如图2). 答案 2.思路如下:如图3,AC为⊙O的直径,联结PC. 由△ACP∽△PAB,得,即.所以. 因此. 所以当x=4时,x-y最大,最大值为2. 图2 图3查看更多