高考数学试卷广东卷评析

高考数学试卷广东卷评析

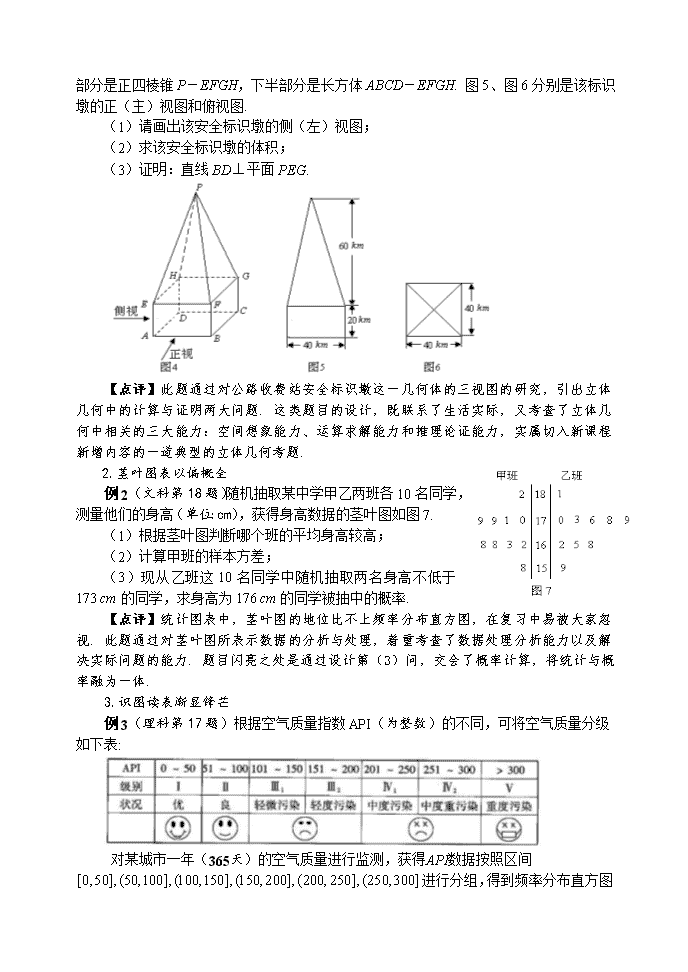
‎2009年高考数学试卷（广东卷）评析 徐 勇（广东省教育厅教研室）‎ 高建彪（广东省中山市东升高中）‎ ‎2009年广东省的高考数学试卷，遵循了《2009年普通高等学校招生全国统一考试新课程标准数学科考试大纲》和《2009年普通高等学校招生全国统一考试数学考试大纲的说明（广东卷）》的要求，沿袭了前两年新课程高考成功的题型结构和试卷模式，重点考查了高中数学的主干知识和方法，命题做到稳中有变，在数学应用及创新上略比前两年有所加强. ‎ 一、整体分析 ‎1. 注重基础 历年高考都十分重视对学生基础知识和基本技能的考查，并力求在客观题部分尽可能覆盖大部分知识点. 下面对2009年高考数学广东卷文、理科的客观题（必做题）进行统计，得到客观题考查的知识点分布情况，具体见表1.‎ 表1：客观题考查的知识点分布情况 集合与 逻辑 函数 数列 三角函数 平面向量 解三角形 不等式 直线和圆 圆锥曲线 立体几何 排列组合概率 统计 框图 导数与 积分 复数 应用 创新 理 题号 ‎1‎ ‎3‎ ‎4‎ ‎6、10‎ ‎11‎ ‎5‎ ‎7、12‎ ‎9‎ ‎2‎ ‎8‎ 分值 ‎5‎ ‎5‎ ‎5‎ ‎10‎ ‎▲‎ ‎5‎ ‎5‎ ‎10‎ ‎▲‎ ‎5‎ ‎▲‎ ‎5‎ ‎5‎ 文 题号 ‎1‎ ‎4‎ ‎5‎ ‎9‎ ‎3‎ ‎7‎ ‎13‎ ‎6‎ ‎12‎ ‎11‎ ‎8‎ ‎2‎ ‎10‎ 分值 ‎5‎ ‎5‎ ‎5‎ ‎5‎ ‎5‎ ‎5‎ ‎5‎ ‎5‎ ‎5‎ ‎5‎ ‎5‎ ‎5‎ ‎5‎ ‎（注：▲部分与其他内容有交会。）‎ 从表1可以看出，客观题覆盖了80%的章节，文科试题以单独考查某一知识点为主，理科试题适度地出现了知识点的交会考查.‎ ‎2. 突出主干 解答题部分是区分选拔优秀人才的主战场，侧重于考查高中数学的主干知识，一般涉及到函数、三角、数列、不等式、立体几何、解析几何、概率统计等七大部分，2009年高考数学广东卷文、理科各6道解答题，均考查了以上主干知识，具体见表2.‎ 表2：解答题考查的知识点分布情况 第16题 第17题 第18题 第19题 第20题 第21题 文科 三角函数 立体几何 概率统计 解析几何 数列 函数 理科 三角函数 概率统计 立体几何 解析几何 函数 数列 ‎（注：理科第21题交会了不等式的考查。）‎ ‎3.重视能力 在考试大纲中，明确指出“能力是指空间想象能力、抽象概括能力、推理论证能力、运算求解能力、数据处理能力以及应用意识和创新意识”. 能力的考查如何在试卷中全面实现呢？一般来说，推理论证能力和抽象概括能力的考查贯穿于全卷，空间想象能力的考查主要体现在对文字语言、符号语言及图形语言的互相转化，运算求解能力的考查主要以代数运算为主，数据处理能力的考查主要是运用概率统计的基本方法和思想解决实际问题的能力，以及对图表数据的处理. 在各项能力的考查中，以运算求解、读表识图、推理论证、应用创新等能力为主，着重考查学生的数学思维能力. 2009年高考数学广东卷 主要考查的各项数学能力见表3.‎ 表3：着重考查的能力与题号对应情况 文科题号 理科题号 运算求解能力 ‎2、3、5、7、8、9、13‎ ‎14、15、16、18、19、20、21‎ ‎4、6、10、11、13、14、15、‎ ‎16、18、19、20、21‎ 数据处理能力 ‎10、12、18‎ ‎12、17‎ 空间想象能力 ‎6、17‎ ‎5、18、‎ 推理论证能力 ‎6、11、17、19、20、21‎ ‎5、9、18、19、20、21‎ 抽象概括能力 ‎1、4‎ ‎1、2、3‎ 应用创新能力 ‎10、12、17、18‎ ‎6、7、8、17‎ ‎（注：按题目着重考查的能力进行统计。）‎ 从上表中可以清楚地看出试卷着重考查的数学能力. 一般地，考查数学能力均以数学知识为载体，从问题入手，侧重考查对知识的理解和应用，特别是综合和灵活地运用，以此来检测考生的迁移能力，检测理性思维的广度和深度，挖掘考生进一步学习的潜能.‎ ‎4.强化思想 中学数学阶段，最为重要的数学思想是数形结合思想、分类讨论思想、等价转化思想和函数与方程思想等. 2009年高考数学广东卷在注重考查基础知识和基本技能的同时，也注重对各项能力和数学核心思想的考查. 最为突出的是对数形结合思想的考查，例如文科第1题、第11题、第12题、第15题、第17题、第18题、第19题和第20题，理科第1题、第6题、第8题、第15题、第19题、第20题和第21题等都考查了数形结合思想。另外分类讨论思想和函数与方程思想也得到了不同程度的考查，例如文科第10题和第21题，理科第17题和第20题等考查了分类讨论思想，文科第4题和第21题，理科第3题、第8题、第12题和第20题等考查了函数与方程思想. 等价转化思想则贯穿于整个试卷的解题过程中. ‎ ‎5.结构稳定 从2007年广东省实施新课程的首届高考以来，连续三年高考数学广东卷均保持一致的试卷结构，具体见表4.‎ 表4：2007～2009年高考数学广东卷连续三年的试卷结构 选择题 填空题 解答题 文科 ‎10个小题 ‎（共50分）‎ 必做题3个，选做题2个，为二选一（共20分）‎ ‎*选考专题：几何证明选讲、坐标系与参数方程 解答题6个 ‎（共80分）‎ 理科 ‎8个小题 ‎（共40分）‎ 必做题4个，选做题3个，为三选二（共30分）‎ ‎*选考专题：在文科选考中增加《不等式选讲》‎ 解答题6个 ‎（共80分）‎ ‎（注：时量120分钟，满分150分。）‎ 选考太多，势必加重教学负担，从而理科三选二，文科二选一。对选考专题内容的处理，在2009年的11份新课程高考数学试卷中，唯独广东卷采用填空题型。选考题采用填空题型，优于选择题型（减少了答题的机遇性），也优于解答题型（降低了学生答题的难度），凸现了广东卷处理选考专题的科学合理性.‎ 二、亮点扫描 ‎1.三视图构筑立体几何 例1（文科第17题）某高速公路收费站入口处的安全标识墩如图4‎ 所示，墩的上半部分是正四棱锥P－EFGH，下半部分是长方体ABCD－EFGH. 图5、图6分别是该标识墩的正（主）视图和俯视图.‎ ‎（1）请画出该安全标识墩的侧（左）视图；‎ ‎（2）求该安全标识墩的体积；‎ ‎（3）证明：直线BD平面PEG.‎ ‎【点评】此题通过对公路收费站安全标识墩这一几何体的三视图的研究，引出立体几何中的计算与证明两大问题. 这类题目的设计，既联系了生活实际，又考查了立体几何中相关的三大能力：空间想象能力、运算求解能力和推理论证能力，实属切入新课程新增内容的一道典型的立体几何考题.‎ ‎2.茎叶图表以偏概全 例2（文科第18题）随机抽取某中学甲乙两班各10名同学，测量他们的身高（单位：cm），获得身高数据的茎叶图如图7.‎ ‎（1）根据茎叶图判断哪个班的平均身高较高；‎ ‎（2）计算甲班的样本方差；‎ ‎（3）现从乙班这10名同学中随机抽取两名身高不低于‎173 cm的同学，求身高为‎176 cm的同学被抽中的概率.‎ ‎【点评】统计图表中，茎叶图的地位比不上频率分布直方图，在复习中易被大家忽视. 此题通过对茎叶图所表示数据的分析与处理，着重考查了数据处理分析能力以及解决实际问题的能力. 题目闪亮之处是通过设计第（3）问，交会了概率计算，将统计与概率融为一体.‎ ‎3.识图读表渐显锋芒 例3（理科第17题）根据空气质量指数API（为整数）的不同，可将空气质量分级如下表: ‎ 对某城市一年（365天）的空气质量进行监测，获得API数据按照区间 进行分组，得到频率分布直方图如图5.‎ ‎（1）求直方图中的值； ‎ ‎（2）计算一年中空气质量分别为良和轻微污染的天数；‎ ‎（3）求该城市某一周至少有2天的空气质量为良或轻微污染的概率.‎ ‎(结果用分数表示．已知,‎ ,）‎ ‎【点评】近年高考数学命题中，逐渐重视对图表分析与处理能力的考查，一份优秀的考卷离不开对图形的研究和对表格的分析. 此题将表与图有机结合，考查了概率统计知识. 不但如此，2009年高考数学广东卷中，还有许多题目涉及到图表的研究，例如文科第1题、第10题、第11题、第12题、第15题、第17题和第18题，理科第1题、第6题、第8题、第9题、第12题、第15题和第18题等，足可见图表的地位在高考中显得越来越重要.‎ ‎4.新增内容标新立异 例4（理科第8题）已知甲、乙两车由同一起点同时出发,并沿同一路线（假定为直线）行驶．甲车、乙车的速度曲线分别为和（如图2所示）．那么对于图中给定的和，下列判断中一定正确的是（ ）。‎ ‎（A）在时刻，甲车在乙车前面 ‎（B）时刻后，甲车在乙车后面 ‎（C）在时刻，两车的位置相同 ‎（D）时刻后，乙车在甲车前面 ‎【点评】对新增内容，如何打破常规而命题，体现一种新颖呢？此题表面上看是函数图象的研究，但实质上是考查定积分的实际意义和几何意义，通过对速度求积分得到路程，进一步将两个路程段的比较转化为曲边梯形面积大小的判断. 不仅是此题新颖，理科第9题考查新课程新增的框图，交会考查了统计中的样本数字特征；文科第17题考查新课程新增的三视图，交会考查了立体几何中的体积计算和线面垂直；文科第18题考查新课程新增茎叶图，交会考查了方差和古典概型. 这些题目的新颖形式都体现了高考命题者在处理新课程新增内容时所追求的一种创新.‎ ‎5.应用创新美酒飘香 例5（文科第10题）广州2010年亚运会火炬传递在A、B、C、D、E五个城市之间进行，各城市之间的路线距离（单位：百公里）见下表. 若以A为起点，E为终点，每个城市经过且只经过一次，那么火炬传递的最短路线距离是（ ）。‎ ‎（A） 20.6 （B）21 （C）22 （D） 23 ‎ ‎ w.w.w.k.s.5.u.c.o.m ‎ ‎【点评】‎ 高考命题时，应用问题的背景应当密切联合生活实际，大部分切入社会中的热点问题. 此题以即将举行的亚运会中火炬传递为切入点，考查了学生处理实际问题的能力，解答时将B、C、D三个城市排列中间的6种情况分别计算出来即可求解，通过分情况讨论及加法计算解决了文科选择题的压轴题.‎ ‎6. 分层抽样老树开花 例6（文科第12题）某单位200名职工的年龄分布情况如图2，现要从中抽取40名职工作样本，用系统抽样法，将全体职工随机按1－200编号，并按编号顺序平均分为40组（1－5号，6－10号…，196－200号）.若第5组抽出的号码为22，则第8组抽出的号码应是 . 若用分层抽样方法，则40岁以下年龄段应抽取 人. ‎ ‎【点评】分层抽样的考题在历届高考数学试卷中都十分经典，形式上也基本一致，但此题打破之前的惯例，交会了对系统抽样的考查，不仅如此，还通过扇形图的切入，考查了分层抽样的计算思维.‎ 三、复习策略 ‎1. 研究对象，周密计划 高三数学复习备考中，既要研透考纲，对教学内容及具体要求清清楚楚，又要研究学生，对学生所掌握的知识水平了如指掌，针对学生的实际情况及考纲要求，制定一份周密的高三数学备考计划. 复习计划的制订，要汲取上届高三数学备考的成功经验，且可操作性一定要强，不能仅是停留在纸上. ‎ ‎2. 贴近教材，夯实基础 新课程实验教学已有几年，目前各类复习资料铺天盖地，但大部分资料都比不上教材上的例题和习题的价值，教材上的A组、B组题，许多是选自历届高考数学试题中的经典考题，例如人教A版《普通高中课程标准实验教科书·数学4（必修）》中“三角恒等变换”一章复习的A组第9～11题，高考考查三角也不过如此. 复习中要做到紧扣教材，举一反三，认真夯实学生的“双基”. 我们必须明确，扎实的数学基础知识，才是学好数学的前提条件和关键所在.‎ ‎3. 突破重点，狠抓落实 高中数学的主干知识，哪些是我们突破的重点，前面已经明确提出. 对于这些主干知识，在高三数学的复习中，必须加强针对性突破，做到一一落实. 同时，关于运算求解能力的培养，也必须狠抓落实，从教师上课对例题的规范板演开始，从学生考试的规范草稿等细节入手，力争计算既快又准，尽量减少答题时的计算失误.‎ ‎4. 查漏补缺，疏通脉络 在高考复习中狠抓基础落实和重点突破的同时，也要做到尽可能地避免遗忘可能的考点，比如茎叶图、统计案例等等，指导学生用好错题订正本，研究清楚历次考试中的错题. 在复习中，既要把各章节的知识形成网络框架，也要把高中数学的所有知识构建成一张基础知识、基本技能、基本思想方法的大网.‎