高考文科数学复习备课课件:第二节 同角三角函数基本关系式与诱导公式
文数
课标版
第二节 同角三角函数基本关系式与诱导公式
1.同角三角函数的基本关系
(1)平方关系:① sin2α+cos2α=1 .
(2)商数关系:② =tan α .
sin
cos
α
α
教材研读
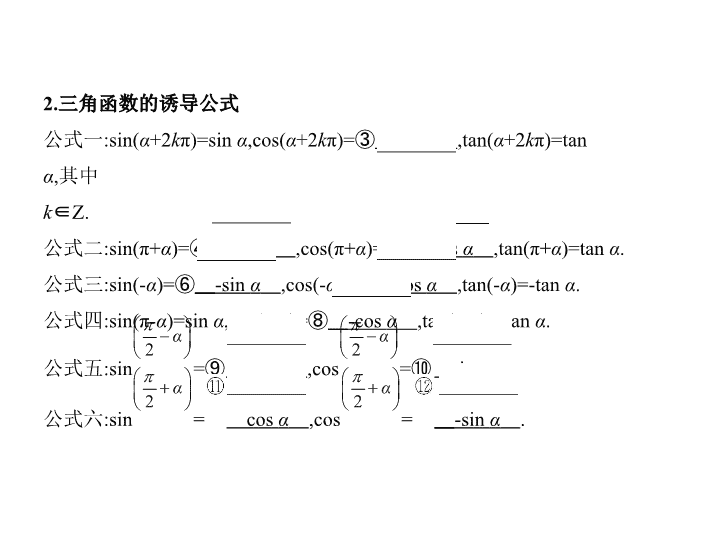
2.三角函数的诱导公式
公式一:sin(α+2kπ)=sin α,cos(α+2kπ)=③ cos α ,tan(α+2kπ)=tan α,其中
k∈Z.
公式二:sin(π+α)=④ -sin α ,cos(π+α)=⑤ -cos α ,tan(π+α)=tan α.
公式三:sin(-α)=⑥ -sin α ,cos(-α)=⑦ cos α ,tan(-α)=-tan α.
公式四:sin(π-α)=sin α,cos(π-α)=⑧ -cos α ,tan(π-α)=-tan α.
公式五:sin =⑨ cos α ,cos =⑩ sin α .
公式六:sin = cos α ,cos = -sin α .
2 α 2 α
2 α 2 α
判断下列结论的正误(正确的打“√”,错误的打“×”)
(1)若α,β为锐角,则sin2α+cos2β=1. (×)
(2)若α∈R,则tan α= 恒成立. (×)
(3)sin(π+α)=-sin α成立的条件是α为锐角. (×)
(4)诱导公式的记忆口诀中“奇变偶不变,符号看象限”,其中的奇、偶
是指 的奇数倍和偶数倍,变与不变指函数名称的变化情况. (√)
sin
cos
α
α
2
1.sin(-600°)的值为 ( )
A. B. C.1 D.
答案 A sin(-600°)=sin(-720°+120°)=sin 120°= .
3
2
2
2
3
3
3
2
2.若cos α= ,α∈ ,则tan α等于 ( )
A.- B. C.-2 D.2
答案 C 由已知得sin α=-
=- =- ,∴tan α= =-2 ,选C.
1
3 ,02
2
4
2
4 2 2
21 cos α
11 9
2 2
3
sin
cos
α
α 2
3.已知tan α=- ,且α为第二象限角,则sin α的值为 ( )
A. B.- C. D.-
答案 C ∵tan α= =- ,
∴cos α=- sin α,
又sin2α+cos2α=1,
∴sin2α+ sin2α= sin2α=1,
又由α为第二象限角知sin α>0,
∴sin α= ,故选C.
5
12
1
5
1
15
5
13
5
13
sin
cos
α
α
5
12
12
5
144
25
169
25
5
13
4.已知tan α=2,则 的值为 .
答案
解析 ∵tan α=2,
∴ = = = .
sin cos
sin cos
α α
α α
1
3
sin cos
sin cos
α α
α α
sin cos
cos cos
sin cos
cos cos
α α
α α
α α
α α
tan 1
tan 1
α
α
1
3
5.已知sin θ+cos θ= ,θ∈ ,则sin θ-cos θ的值为 .
答案 -
解析 由题意知(sin θ+cos θ)2= ,∴1+2sin θcos θ= ,
4
3 0, 4
2
3
16
9
16
9
∴2sin θcos θ= ,∴(sin θ-cos θ)2=1-2sin θcos θ=1- = ,可得sin θ-cos θ=±
.又∵θ∈ ,∴sin θ
0,cos α<0,∴sin α-cos α>0.
∴sin α-cos α= .
24
25
49
25
12
25
7
5
∵tan α=- ,
∴ = = =- .
4
3
2 2
1
cos sinα α
2
2
tan 1
1 tan
α
α
2
2
4 13
41 3
25
7
由 得
∴tan α=- .
(2) = = = .
1sin cos ,5
7sin cos ,5
α α
α α
4sin ,5
3cos ,5
α
α
4
3
2 2
1
cos sinα α
2 2
2 2
sin cos
cos sin
α α
α α
2 2
2
2 2
2
sin cos
cos
cos sin
cos
α α
α
α α
α
2
2
tan 1
1 tan
α
α
规律总结
(1)利用sin2α+cos2α=1可以实现角α的正弦、余弦的互化,利用 =tan α
可以实现角α的弦切互化.
(2)对于sin α+cos α,sin αcos α,sin α-cos α这三个式子,利用(sin α±cos α)2=
1±2sin αcos α,可以知一求二.
(3)注意对sin2α+cos2α=1的逆用及变形应用:1=sin2α+cos2α,sin2α=1-cos2α,
cos2α=1-sin2α.
sin
cos
α
α
变式1-1 保持本例条件不变,求:
(1) 的值;
(2)sin2α+2sin αcos α的值.
解析 tan α=- ,则:
(1) = = = .
(2)sin2α+2sin αcos α= = = =- .
sin 4cos
5sin 2cos
α α
α α
4
3
sin 4cos
5sin 2cos
α α
α α
tan 4
5tan 2
α
α
4 43
45 23
8
7
2
2 2
sin 2sin cos
sin cos
α α α
α α
2
2
tan 2tan
tan 1
α α
α
16 8
9 3
16 19
8
25
1-2 (2016江苏南京模拟)已知α为第二象限角,则cos α +
sin α = .
答案 0
解析 原式=cos α +sin α =cos α· +sin α·
,
因为α是第二象限角,所以sin α>0,cos α<0,
所以cos α· +sin α· =-1+1=0,即原式等于0.
21 tan α
2
11 tan α
2 2
2
sin cos
cos
α α
α
2 2
2
sin cos
sin
α α
α
1
| cos |α
1
| sin |α
1
| cos |α
1
| sin |α
考点二 三角函数的诱导公式
典例2 (1)若sin α是方程5x2-7x-6=0的根,则
= ( )
A. B. C. D.
(2)sin(-1 200°)cos 1 290°+cos(-1 020°)sin(-1 050°)= .
23 3sin sin tan (2 )2 2
cos cos sin( )2 2
α α α
α α α
3
5
5
3
4
5
5
4
解析 (1)方程5x2-7x-6=0的两根为x1=- ,x2=2,
则sin α=- ,
所以原式= =- = .
(2)原式=-sin 1 200°cos 1 290°-cos 1 020°sin 1 050°
=-sin(3×360°+120°)cos(3×360°+210°)-cos(2×360°+300°)sin(2×360°+
330°)
=-sin 120°cos 210°-cos 300°sin 330°
=-sin(180°-60°)cos(180°+30°)-cos(360°-60°)sin(360°-30°)
=sin 60°cos 30°+cos 60°sin 30°
= × + × =1.
3
5
3
5
2cos ( cos )tan
sin ( sin )( sin )
α α α
α α α
1
sin α
5
3
3
2
3
2
1
2
1
2
答案 (1)B (2)1
1.巧用相关角的关系会简化解题过程.常见的具有互余关系的角有 -α
与 +α, +α与 -α, +α与 -α等,常见的具有互补关系的角有 +θ与
-θ, +θ与 -θ等.
3
6
3
6
4
4
3
2
3
4
3
4
规律总结
2.用诱导公式化简求值,应遵循:
(1)“负化正”,运用诱导公式将负角的三角函数化为正角的三角函数.
(2)“大化小”,利用诱导公式将大于360°的角的三角函数化为0°到360°
的角的三角函数.
(3)“小化锐”,将大于90°的角的三角函数化为0°到90°的角的三角函
数.
(4)“锐求值”,得到0°到90°的角的三角函数后,若是特殊角,则可直接求
得,若是非特殊角,则可由计算器求得.
2-1 若cos =- ,则sin = .
答案
解析 ∵cos =- , - = ,即α- = - ,
∴sin =sin =-sin
=-cos = .
3 α
1
3 6α
1
3
3 α
1
3 3 α 6α 2
6
3 α 2
6α 3 2α 2 3 α
3 α
1
3
2-2 已知cos = ,则cos -sin2 的值为 .
答案 -
解析 因为cos =cos =-cos =- ,
sin2 =sin2 =sin2 =1-cos2 =1- = ,
所以cos -sin2 =- - =- .
6 α
3
3
5
6 α 6α
2 3
3
5
6 α 6 α 6 α
3
3
6α 6 α 6 α 6 α
2
3
3
2
3
5
6 α 6α
3
3
2
3
2 3
3
考点三 三角函数式的化简与求值
典例3 (1)已知A= + (k∈Z),则A的值构成的集合是
( )
A.{1,-1,2,-2} B.{-1,1}
C.{2,-2} D.{1,-1,0,2,-2}
(2) = .
答案 (1)C (2)-1
解析 (1)当k为偶数时,A= + =2;
当k为奇数时,A= - =-2.
sin( )
sin
k α
α
cos( )
cos
k α
α
3tan( )cos(2 )sin 2
cos( 3 )sin( 3 )
α α α
α α
sin
sin
α
α
cos
cos
α
α
sin
sin
α
α
cos
cos
α
α
∴A的值构成的集合是{2,-2}.
(2)原式=
=
=
=-
=- ·
=-1.
tan cos sin 2 2
cos(3 )[ sin(3 )]
α α α
α α
tan cos sin 2
( cos )sin
α α α
α α
tan cos cos
( cos )sin
α α α
α α
tan cos
sin
α α
α
sin
cos
α
α
cos
sin
α
α
方法技巧
1.利用诱导公式把任意角的三角函数转化为锐角三角函数的步骤
任意负角的三角函数 任意正角的三角函数 0°到360°
的角的三角函数 锐角三角函数
也就是:“负化正,大化小,化到锐角就好了”.
2.利用诱导公式化简三角函数的要求
(1)化简过程是恒等变形;
(2)结果要求项数尽可能少,次数尽可能低,结构尽可能简单,能求值的要
求出值.
3-1 若f(α)= (k∈Z),则f(2 017)= .
答案 -1
解析 ①当k为偶数时,设k=2n(n∈Z),原式=
= =-1;
②当k为奇数时,设k=2n+1(n∈Z),原式=
= =-1.
综上所述,当k∈Z时, f(α)=-1,故f(2 017)=-1.
sin[( 1) ] cos[( 1) ]
sin( ) cos( )
k α k α
k α k α
sin(2 ) cos(2 )
sin( ) cos
n α n α
α α
sin( ) cos( )
sin cos
α α
α α
sin[(2 2) ] cos[(2 2) ]
sin[(2 1) ] cos[(2 1) ]
n α n α
n α n α
sin cos( )
sin( ) cos( )
α α
α α
3-2 已知α为第三象限角, f(α)= .
(1)化简f(α);
(2)若cos = ,求f(α)的值.
解析 (1)f(α)=
= =-cos α.
(2)∵cos = ,∴-sin α= ,从而sin α=- .
又α为第三象限角,∴cos α=- =- ,
3sin cos tan( )2 2
tan( ) sin( )
α α α
α α
3
2α
1
5
3sin cos tan( )2 2
tan( ) sin( )
α α α
α α
( cos ) sin ( tan )
( tan ) sin
α α α
α α
3
2α
1
5
1
5
1
5
21 sin α 2 6
5
∴f(α)= .2 6
5