高考文科数学复习备课课件：第七节　抛物线

高考文科数学复习备课课件：第七节　抛物线

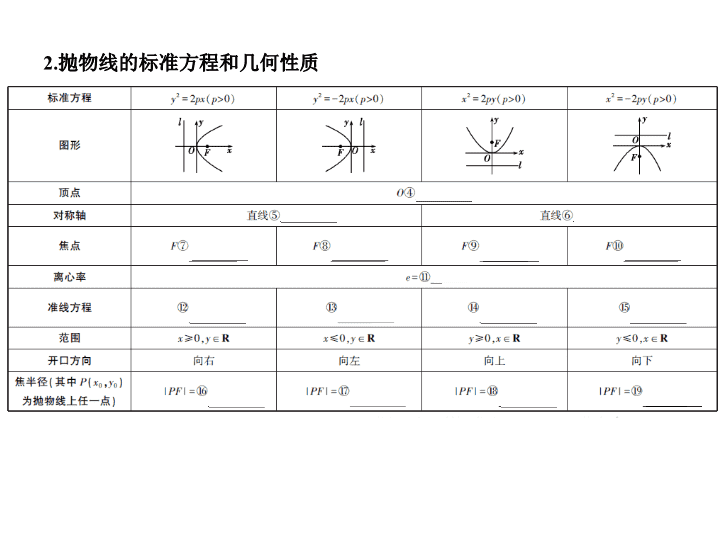
文数 课标版 第七节　抛物线 1.抛物线的概念 平面内与一个定点 F 和一条定直线 l ( l 不经过点 F )距离① 　相等     的点 的轨迹叫做抛物线.点 F 叫做抛物线的② 　焦点     .直线 l 叫做抛物线的 ③ 　准线     . 教材研读 2.抛物线的标准方程和几何性质   判断下列结论的正误(正确的打“√”,错误的打“ × ”) (1)平面内与一个定点 F 和一条定直线 l 的距离相等的点的轨迹一定是抛 物线.   ( × ) (2)抛物线 y =4 x 2 的焦点坐标为(2,0).   ( × ) (3)若一抛物线过点 P (2,3),其标准方程可设为 y 2 =2 px ( p >0)或 x 2 =2 py ( p >0).   (√) (4)抛物线既是中心对称图形,又是轴对称图形.   ( × ) (5)过抛物线的焦点与抛物线对称轴垂直的直线被抛物线截得的线段叫 做抛物线的通径,那么抛物线 x 2 =-2 ay ( a >0)的通径长为2 a .   (√) 1.若点 P 到点 F (0,2)的距离比它到直线 y +4=0的距离小2,则 P 的轨迹方程 为   (　　) A. y 2 =8 x 　    B. y 2 =-8 x 　    C. x 2 =8 y 　    D. x 2 =-8 y 答案     C     P 到 F (0,2)的距离比它到直线 y +4=0的距离小2,因此 P 到 F (0,2) 的距离与它到直线 y +2=0的距离相等,故 P 的轨迹是以 F 为焦点, y =-2为准 线的抛物线,所以 P 的轨迹方程为 x 2 =8 y . 2.抛物线 y =2 x 2 的焦点坐标是   (　　) A.   　    B.   　    C.   　    D.   答案     C　抛物线的标准方程为 x 2 =   y ,所以焦点坐标是   . 3.抛物线的顶点在原点,准线方程为 x =-2,则抛物线方程是   (　　) A. y 2 =-8 x 　    B. y 2 =-4 x 　     C. y 2 =8 x 　    D. y 2 =4 x 答案     C　由抛物线的顶点在原点,准线方程为 x =-2,知 p =4,且开口向右, 故抛物线方程为 y 2 =8 x . 4.若抛物线 y =4 x 2 上的一点 M 到焦点 F 的距离为1,则点 M 的纵坐标是   (    　) A.   　    B.   　    C.   　    D.0 答案     B　抛物线的标准方程为 x 2 =   y , M 到准线的距离等于 M 到焦点的 距离,又准线方程为 y =-   , 设 M ( x , y ),则 y +   =1,∴ y =   . 5.已知抛物线关于 x 轴对称,它的顶点在坐标原点 O ,并且经过点 M (2, y 0 ). 若点 M 到该抛物线焦点 F 的距离为3,则| OM |= 　　　     . 答案 　2   解析 　由题意可设抛物线方程为 y 2 =2 px ( p >0). 由| MF |=   +2=3得 p =2, ∴抛物线方程为 y 2 =4 x . ∴点 M 的坐标为(2, ± 2   ), ∴| OM |=   =2   . 考点一　抛物线的标准方程及几何性质 典例1 　(1)(2015陕西,3,5分)已知抛物线 y 2 =2 px ( p >0)的准线经过点(-1,1), 则该抛物线焦点坐标为   (　　) A.(-1,0)　    B.(1,0)　    C.(0,-1)　    D.(0,1) (2)若抛物线的顶点在原点,开口向上, F 为焦点, M 为准线与 y 轴的交点, A 为抛物线上一点,且| AM |=   ,| AF |=3,则此抛物线的标准方程为 　　     　　　     . 答案 　(1)B　(2) x 2 =8 y 或 x 2 =4 y 解析 　(1)抛物线 y 2 =2 px ( p >0)的准线方程为 x =-   , 由题设知-   =-1,即   =1, 考点突破 所以焦点坐标为(1,0).故选B. (2)设所求抛物线的标准方程为 x 2 =2 py ( p >0), A ( x 1 , y 1 ),则 F   , M   , 则   ⇒ p =4或 p =2. 故所求抛物线的标准方程为 x 2 =8 y 或 x 2 =4 y . 方法技巧 (1) 抛物线的标准方程有四种不同的形式 , 要掌握焦点到准线的距离 , 顶 点到准线、焦点的距离 , 通径长与标准方程中系数 2 p 的关系 . (2)求标准方程要先确定形式,必要时要进行分类讨论,标准方程有时可 设为 y 2 = mx 或 x 2 = my ( m ≠ 0). (3)焦点到准线的距离简称为焦准距,抛物线 y 2 =2 px ( p >0)上的点常设为   . 1-1 　已知直线 l 过抛物线 C 的焦点,且与 C 的对称轴垂直, l 与 C 交于 A , B 两 点,| AB |=12, P 为 C 的准线上一点,则△ ABP 的面积为   (　　) A.18　    B.24　    C.36　    D.48 答案     C　不妨设抛物线方程为 y 2 =2 px ( p >0). ∵当 x =   时,| y |= p ,∴ p =   =   =6. 又 P 到直线 AB 的距离为 p , ∴ S △ ABP =   × 12 × 6=36. 1-2　 若抛物线的焦点为直线3 x -4 y -12=0与坐标轴的交点,求抛物线的标 准方程. 解析　 对于直线方程3 x -4 y -12=0,令 x =0,得 y =-3,令 y =0,得 x =4,所以抛物线 的焦点坐标为(0,-3)或(4,0). 当焦点坐标为(0,-3)时,设方程为 x 2 =-2 py ( p >0),则   =3,所以 p =6,此时抛物 线的标准方程为 x 2 =-12 y ; 当焦点坐标为(4,0)时,设方程为 y 2 =2 px ( p >0),则   =4, 所以 p =8,此时抛物线的标准方程为 y 2 =16 x . 所以所求抛物线的标准方程为 x 2 =-12 y 或 y 2 =16 x . 考点二　抛物线的定义及其应用 典例2 　(1)(2016江西赣州模拟)若点 A 的坐标为(3,2), F 是抛物线 y 2 =2 x 的 焦点,点 M 在抛物线上移动时,使| MF |+| MA |取得最小值的 M 的坐标为   (　　) A.(0,0)　    B.   　    C.(1,   )　    D.(2,2) (2)已知 M 是抛物线 x 2 =4 y 上一点, F 为其焦点,点 A 在圆 C :( x +1) 2 +( y -5) 2 =1 上,则| MA |+| MF |的最小值是 　　　     . (3)已知直线 l 1 :4 x -3 y +6=0和直线 l 2 : x =-1,抛物线 y 2 =4 x 上一动点 P 到直线 l 1 和直线 l 2 的距离之和的最小值是 　　　     . 答案 　(1)D　(2)5　(3)2 解析 　(1)过 M 点作准线的垂线,垂足是 N ,则| MF |+| MA |=| MN |+| MA |, 当 A , M , N 三点共线时,| MF |+| MA |取得最小值,此时 M (2,2). (2)依题意,由点 M 向抛物线 x 2 =4 y 的准线 l : y =-1引垂线,垂足为 M 1 ,则有| MA | +| MF |=| MA |+| MM 1 |,结合图形可知| MA |+| MM 1 |的最小值等于圆心 C (-1,5) 到 y =-1的距离再减去圆 C 的半径,即等于6-1=5,因此| MA |+| MF |的最小值 是5. (3)易知 l 2 : x =-1是抛物线 y 2 =4 x 的准线,设抛物线的焦点为 F (1,0),则动点 P 到 l 2 的距离等于| PF |,则动点 P 到直线 l 1 和直线 l 2 的距离之和的最小值为焦 点 F 到直线 l 1 :4 x -3 y +6=0的距离,所以最小值是   =2. 方法指导 与抛物线有关的最值问题,一般情况下都与抛物线的定义有关.由于抛 物线的定义在运用上有较大的灵活性,因此此类问题也有一定的难度. “看到准线想焦点,看到焦点想准线”,这是解决抛物线焦点弦有关问 题的重要途径. 2-1     (2014课标Ⅰ,10,5分)已知抛物线 C : y 2 = x 的焦点为 F , A ( x 0 , y 0 )是 C 上一 点,| AF |=   x 0 ,则 x 0 =   (　　) A.1　    B.2　    C.4　    D.8 答案     A　由 y 2 = x 得2 p =1,即 p =   ,因此焦点 F   ,准线方程为 l : x =-   ,设 点 A 到准线的距离为 d ,由抛物线的定义可知 d =| AF |,从而 x 0 +   =   x 0 ,解得 x 0 =1,故选A. 2-2     已知点 P 是抛物线 y 2 =2 x 上的一个动点,则点 P 到点(0,2)的距离与点 P 到该抛物线准线的距离之和的最小值为(　　) A.   　    B.3　    C.   　    D.   答案     A　易知抛物线 y 2 =2 x 的焦点为 F   ,由抛物线的定义知点 P 到 焦点 F 的距离等于它到准线的距离,因此要求点 P 到点(0,2)的距离与点 P 到抛物线的准线的距离之和的最小值,可以转化为求点 P 到点(0,2)的距 离与点 P 到焦点 F 的距离之和的最小值,结合图形不难得出相应的最小 值就等于焦点 F 到点(0,2)的距离.因此所求的最小值等于   =   ,选A. 2-3     (2014湖南,15,5分)如图,正方形 ABCD 和正方形 DEFG 的边长分别 为 a , b ( a < b ),原点 O 为 AD 的中点,抛物线 y 2 =2 px ( p >0)经过 C , F 两点,则   = 　　     .   答案 　1+   解析 　由题意知| OD |=   ,| DE |= b ,| DC |= a ,| EF |= b , 故 C   , F   , 又抛物线 y 2 =2 px ( p >0)经过 C 、 F 两点, ∴   ∴   ∴   -2·   -1=0, 又   >1, ∴   =1+   . 考点三　焦点弦问题 典例3　 已知过抛物线 y 2 =2 px ( p >0)的焦点,斜率为2   的直线交抛物线 于 A ( x 1 , y 1 ), B ( x 2 , y 2 )( x 1 < x 2 )两点,且| AB |=9. (1)求该抛物线的方程; (2) O 为坐标原点, C 为抛物线上一点,若   =   + λ   ,求 λ 的值. 解析 　(1)直线 AB 的方程是 y =2     , 与 y 2 =2 px 联立,从而有4 x 2 -5 px + p 2 =0, 所以 x 1 + x 2 =   .由抛物线定义得| AB |= x 1 + x 2 + p =9, 所以 p =4,从而抛物线方程是 y 2 =8 x . (2)由 p =4,4 x 2 -5 px + p 2 =0可简化为 x 2 -5 x +4=0,又 x 1 < x 2 , 从而 x 1 =1, x 2 =4, y 1 =-2   , y 2 =4   , 从而 A (1,-2   ), B (4,4   ). 设   =( x 3 , y 3 )=(1,-2   )+ λ (4,4   )=(4 λ +1,4   λ -2   ), 又   =8 x 3 , 即[2   (2 λ -1)] 2 =8(4 λ +1), 即(2 λ -1) 2 =4 λ +1,解得 λ =0或 λ =2. 方法指导 求抛物线焦点弦的三种方法: ①定义法:| AB |= x 1 + x 2 + p ; ②倾斜角法:| AB |=   ( θ 为 AB 的倾斜角); ③斜率法:| AB |=   × 2 p ( k 为 AB 的斜率). 3-1 　设抛物线 y 2 =2 px ( p >0)的焦点为 F ,经过点 F 的直线交抛物线于 A 、 B 两点,点 C 在抛物线的准线上,且 BC ∥ x 轴.证明:直线 AC 经过原点 O . 证明 　设 AB : x = my +   ,代入 y 2 =2 px , 得 y 2 -2 pmy - p 2 =0. 由根与系数的关系,得 y A y B =- p 2 ,即 y B =-   . ∵ BC ∥ x 轴,且 C 在准线 x =-   上,∴ C   , 则 k OC =   =   =   =   = k OA , ∴直线 AC 经过原点 O . 考点四　直线与抛物线的位置关系 典例4 　已知抛物线 y 2 =2 px ( p >0),过点 C (-2,0)的直线 l 交抛物线于 A 、 B 两 点,坐标原点为 O ,   ·   =12. (1)求抛物线的方程; (2)当以| AB |为直径的圆与 y 轴相切时,求直线 l 的方程. 解析 　(1)显然直线 l 的斜率存在. 设 l : x = my -2,代入 y 2 =2 px 中, 得 y 2 -2 pmy +4 p =0.   (*) 设 A ( x 1 , y 1 ), B ( x 2 , y 2 ),则 y 1 + y 2 =2 pm , y 1 y 2 =4 p , 则 x 1 x 2 =   =4. 因为   ·   =12,所以 x 1 x 2 + y 1 y 2 =12,即4+4 p =12, 解得 p =2,故抛物线的方程为 y 2 =4 x . (2)由(1)可得 y 1 + y 2 =4 m , y 1 y 2 =8,设 AB 的中点为 M , 则| AB |=2 x M = x 1 + x 2 = m ( y 1 + y 2 )-4=4 m 2 -4,   ① 又| AB |=   | y 1 - y 2 |=   ,   ② 由①②得(1+ m 2 )(16 m 2 -32)=(4 m 2 -4) 2 , 解得 m 2 =3,即 m = ±   , 所以直线 l 的方程为 x +   y +2=0或 x -   y +2=0. 方法指导 (1)直线与抛物线的位置关系和直线与椭圆、双曲线的位置关系类似, 一般要用到根与系数的关系. (2)有关直线与抛物线相交的弦长问题,要注意直线是否过抛物线的焦 点,若过抛物线的焦点,可直接使用公式| AB |=| x A |+| x B |+ p 或| AB |=| y A |+| y B |+ p , 若不过焦点,则必须用一般弦长公式. (3)涉及抛物线的弦长、中点、距离等相关问题时,一般利用根与系数 的关系采用“设而不求”“整体代入”等解法. [提醒]涉及弦的中点、斜率时一般用“点差法”求解. 4-1 　已知抛物线 y 2 =4 x 的焦点为 F ,过点 F 的直线交抛物线于 A , B 两点. (1)若   =2   ,求直线 AB 的斜率; (2)设点 M 在线段 AB 上运动,原点 O 关于点 M 的对称点为 C ,求四边形 OACB 面积的最小值. 解析 　(1)依题意知 F (1,0),设直线 AB 的方程为 x = my +1. 将直线 AB 的方程与抛物线的方程联立,消去 x 得 y 2 -4 my -4=0. 设 A ( x 1 , y 1 ), B ( x 2 , y 2 ), 所以 y 1 + y 2 =4 m , y 1 y 2 =-4,   ① 因为   =2   , 所以 y 1 =-2 y 2 .   ② 联立①和②,消去 y 1 , y 2 ,得 m = ±   . 所以直线 AB 的斜率是 ± 2   . (2)由点 C 与原点 O 关于点 M 对称,得 M 是线段 OC 的中点, 从而点 O 与点 C 到直线 AB 的距离相等,所以四边形 OACB 的面积等于2 S △ AOB . 因为2 S △ AOB =2 ×   ·| OF |·| y 1 - y 2 |=   =4   ,所以当 m =0时,四 边形 OACB 的面积最小,最小值为4.