人教版八年级数学上册第十四章测试题及答案

人教版八年级数学上册第十四章测试题及答案

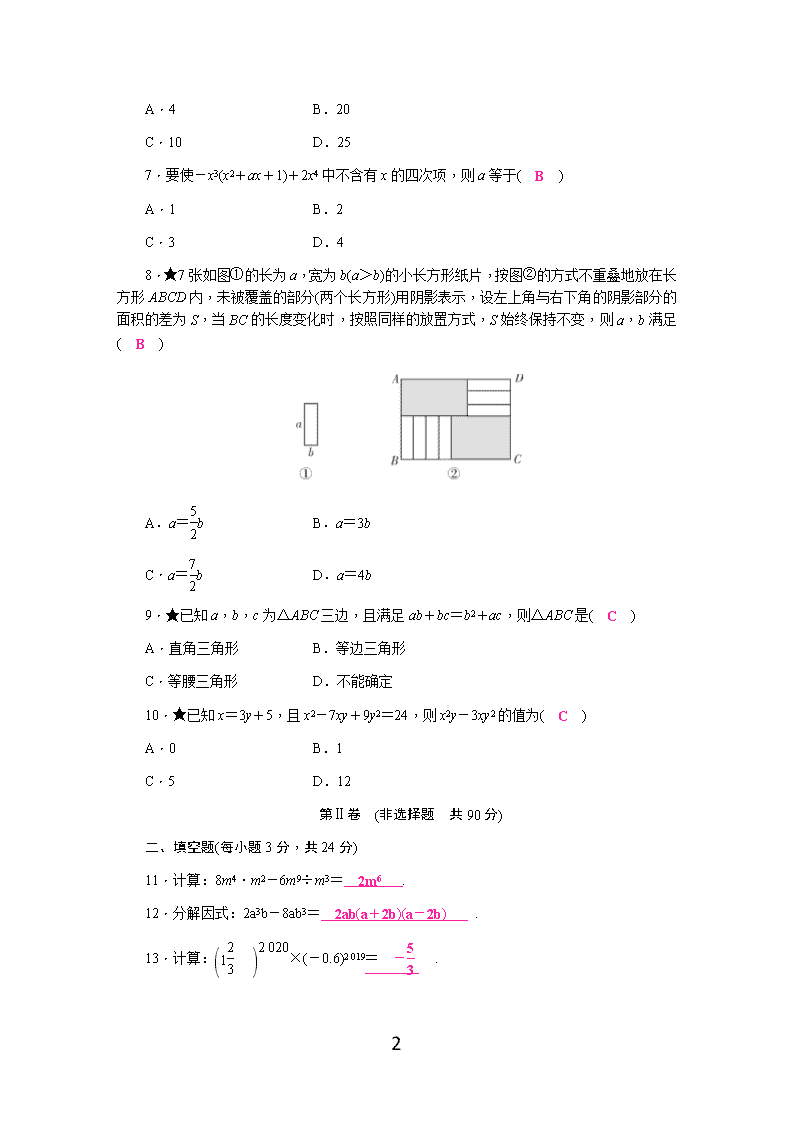
人教版八年级数学上册第十四章测试题及答案 ‎(考试时间：120分钟　　　满分：120分)‎ 分数：__________‎ 1‎ 第Ⅰ卷　(选择题　共30分)‎ 一、选择题(每小题3分，共30分)‎ ‎1．多项式12a3b2c－6ab2－18a2b2的公因式是(　C　)‎ A．6a3b2c B．6ab2c C．6ab2 D．－18a3b2c ‎2．下列运算中正确的是(　D　)‎ A．m12÷m6＝m2‎ B．(m4)3＝m7‎ C．(a－b)2＝a2－b2‎ D．4x3·(－3x3)＝－12x6‎ ‎3．如果a2n－1·an＋5＝a16，那么n的值为(　B　)‎ A．3 B．4 ‎ C．5 D．6‎ ‎4．若4m2＋amn＋25n2是一个完全平方式，则a＝(　C　)‎ A．20 B．－20‎ C．±20 D．±10‎ ‎5．下列各式中，能用平方差公式计算的是(　D　)‎ A．(m－n)(n－m)‎ B．(－a＋1)(a－1)‎ C．(x＋1)(－x－1)‎ D．(a－b＋c)(a＋b－c)‎ ‎6．若m＋n＝－2，则5m2＋5n2＋10mn的值是(　B　)‎ 7‎ A．4 B．20 ‎ C．10 D．25‎ ‎7．要使－x3(x2＋ax＋1)＋2x4中不含有x的四次项，则a等于(　B　)‎ A．1 B．2‎ C．3 D．4‎ ‎8．★7张如图①的长为a，宽为b(a＞b)的小长方形纸片，按图②的方式不重叠地放在长方形ABCD内，未被覆盖的部分(两个长方形)用阴影表示，设左上角与右下角的阴影部分的面积的差为S，当BC的长度变化时，按照同样的放置方式，S始终保持不变，则a，b满足(　B　)‎ A．a＝b B．a＝3b C．a＝b D．a＝4b ‎9．★已知a，b，c为△ABC三边，且满足ab＋bc＝b2＋ac，则△ABC是(　C　)‎ A．直角三角形 B．等边三角形 C．等腰三角形 D．不能确定 ‎10．★已知x＝3y＋5，且x2－7xy＋9y2＝24，则x2y－3xy2的值为(　C　)‎ A．0 B．1‎ C．5 D．12‎ 第Ⅱ卷　(非选择题　共90分)‎ 二、填空题(每小题3分，共24分)‎ ‎11．计算：8m4·m2－6m9÷m3＝ 2m6 .‎ ‎12．分解因式：2a3b－8ab3＝ 2ab(a＋2b)(a－2b) .‎ ‎13．计算：×(－0.6)2 019＝ － .‎ ‎14．已知am＝3，an＝4，则a3m－2n＝ .‎ 7‎ ‎15．已知(x2＋px＋8)(x2－3x＋q)(其中p，q为常数)的计算结果中不含x3和x2项，则p2＋q2＝ 10 .‎ ‎16．若x2＋y2＝10，xy＝3，则x＋y＝ ±4 .‎ ‎17．已知ab＝2，a－b＝3，则a3b－2a2b2＋ab3＝ 18 .‎ ‎18．★观察下列等式：‎ ‎39×41＝402－12，48×52＝502－22，‎ ‎56×64＝602－42，65×75＝702－52，‎ ‎83×97＝902－72，……‎ 请你将发现的规律用含有m，n的式子表示出来：m·n＝ － .‎ 选择、填空题答题卡 一、选择题(每小题3分，共30分)‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ 得分 答案 C D B C D 题号 ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ 答案 B B B C C 二、填空题(每小题3分，共24分)得分：______‎ ‎11． 2m6 　　12. 2ab(a＋2b)(a－2b) ‎ ‎13． － 14. 　15. 10 ‎ ‎16． ±4 17. 18　‎ ‎18． － ‎ 三、解答题(共66分)‎ ‎19．(12分)计算下列各式．‎ ‎(1)(－3xyz)2·x3(x2y)2÷(3x2y2)2；‎ 7‎ 解：原式＝9x2y2z2·x3·x4y2÷(9x4y4)‎ ‎＝x5z2.‎ ‎(2)m2n(mn－7)－7mn(m2n－m)；‎ 解：原式＝m3n2－7m2n－7m3n2＋7m2n ‎＝－6m3n2.‎ ‎(3)(2a＋b)(2a－b)＋(a＋b)2－2(2a2－ab)．‎ 解：原式＝4a2－b2＋a2＋2ab＋b2－4a2＋2ab ‎＝a2＋4ab.‎ ‎20．(8分)计算：‎ ‎(1)12×11；‎ 解：原式＝ ‎＝122－ ‎＝143.‎ ‎(2)7.52＋2.52－5×7.5.‎ 解：原式＝(7.5－2.5)2‎ ‎＝52‎ ‎＝25.‎ ‎21．(12分)将下列各式分解因式．‎ ‎(1)a2－b2＋9a－9b；‎ 解：原式＝(a－b)(a＋b＋9)．‎ 7‎ ‎(2)x2＋y2－xy；‎ 解：原式＝.‎ ‎(3)(m2－5)2＋8(5－m2)＋16.‎ 解：原式＝(m＋3)2(m－3)2.‎ ‎22．(7分)先化简，再求值：‎ ‎[(3x＋2y)(3x－2y)＋(2y＋x)(2y－3x)]÷4x，其中x＝2，y＝－1.‎ 解：原式＝x－y.‎ 当x＝2，y＝－1时，原式＝4.‎ ‎23．(7分)已知多项式A＝(3－2x)(1＋x)＋(3x5y2＋4x6y2－x4y2)÷(x2y)2.‎ ‎(1)化简多项式A；‎ ‎(2)若(x＋1)2＝6，求A的值．‎ 解：(1)A＝(3＋3x－2x－2x2)＋(3x5y2＋4x6y2－x4y2)÷x4y2‎ ‎＝3＋x－2x2＋3x＋4x2－1‎ ‎＝2x2＋4x＋2.‎ ‎(2)由(x＋1)2＝6得x2＋2x＝5，‎ ‎∴2x2＋4x＝10，‎ ‎∴A＝2x2＋4x＋2＝10＋2＝12.‎ ‎24．(10分)探究活动：‎ ‎(1)如图①，可以求出阴影部分的面积是 a2－b2 (写成两数平方差的形式)；‎ 7‎ ‎(2)如图②，若将图①中阴影部分裁剪下来，重新拼成一个长方形，面积是 (a＋b)(a－b) (写成多项式乘法的形式)；‎ ‎(3)比较图①，图②阴影部分的面积，可以得到公式 (a＋b)(a－b)＝a2－b2 .‎ 知识应用：运用你得到的公式解决以下问题：‎ ‎(1)计算：(a＋b－2c)(a＋b＋2c)；‎ ‎(2)若4x2－9y2＝10，4x＋6y＝4，求2x－3y的值．‎ 解：(1)(a＋b－2c)(a＋b＋2c)‎ ‎＝(a＋b)2－4c2‎ ‎＝a2＋2ab＋b2－4c2.‎ ‎(2)∵4x2－9y2＝10，‎ ‎∴(2x＋3y)(2x－3y)＝10.‎ ‎∵4x＋6y＝4，即2x＋3y＝2，‎ ‎∴2x－3y＝5.‎ ‎25．(10分)阅读以下材料：‎ 对数的创始人是苏格兰数学家纳皮尔(J.Nplcr，1550～1617年)，纳皮尔发明对数是在指数书写方式之前，直到18世纪瑞士数学家欧拉(Evlcr，1707～1783年)才发现指数与对数之间的联系．‎ 对数的定义：一般地，若ax＝N(a＞0，a≠1)，那么x叫做以a为底N的对数，记作：x＝logaN.比如指数式24＝16可以转化为4＝log216，对数式2＝log525可以转化为52＝25.‎ 我们根据对数的定义可得到对数的一个性质：loga(M·N)＝logaM＋logaN(a＞0，a≠1，M＞0，N＞0)．理由如下：‎ 设logaM＝m，logaN＝n，则M＝am，N＝an，‎ ‎∴M·N＝am·an＝am＋n，由对数的定义得m＋n＝loga(M·N)．‎ ‎∵m＋n＝logaM＋logaN，‎ 7‎ ‎∴loga(M·N)＝logaM＋logaN.‎ 解决以下问题：‎ ‎(1)将指数43＝64转化为对数式 3＝log464 ；‎ ‎(2)证明：loga＝logaM－logaN(a＞0，a≠1，M＞0，N＞0)；‎ ‎(3)拓展运用：计算log32＋log36－log34＝ 1 .‎ ‎(2)证明：设logaM＝m，logaN＝n，‎ 则M＝am，N＝an，‎ ‎∴＝＝am－n，‎ 由对数的定义得m－n＝loga，‎ ‎∵m－n＝logaM－logaN，‎ ‎∴loga＝logaM－logaN ‎(a＞0，a≠1，M＞0，N＞0)．‎ 7‎