2006年辽宁省高考数学试卷(文科)【附答案、word版本,可再编辑;B4纸型两栏】
2006年辽宁省高考数学试卷(文科)
一、选择题(共12小题,每小题5分,满分60分)
1. 函数y=sin(12x+3)的最小正周期是( )
A.π2 B.π C.2π D.4π
2. 设集合A={1, 2},则满足A∪B={1, 2, 3}的集合B的个数是( )
A.1 B.3 C.4 D.8
3. 设f(x)是R上的任意函数,则下列叙述正确的是( )
A.f(x)f(-x)是奇函数 B.f(x)|f(-x)|是奇函数
C.f(x)-f(-x)是偶函数 D.f(x)+f(-x)是偶函数
4. C61+C62+C63+C64+C65的值为( )
A.61 B.62 C.63 D.64
5. 方程2x2-5x+2=0的两个根可分别作为( )
A.一椭圆和一双曲线的离心率 B.两抛物线的离心率
C.一椭圆和一抛物线的离心率 D.两椭圆的离心率
6. 给出下列四个命题:
①垂直于同一直线的两条直线互相平行.
②垂直于同一平面的两个平面互相平行.
③若直线l1,l2与同一平面所成的角相等,则l1,l2互相平行.
④若直线l1,l2是异面直线,则与l1,l2都相交的两条直线是异面直线.
其中假命题的个数是( )
A.1 B.2 C.3 D.4
7. 双曲线x2-y2=4的两条渐近线与直线x=3围成一个三角形区域,表示该区域的不等式组是( )
A.x-y≥0x+y≥00≤x≤3 B.x-y≥0x+y≤00≤x≤3
C.x-y≤0x+y≤00≤x≤3 D.x-y≤0x+y≥00≤x≤3
8. 设⊕是R上的一个运算,A是R的非空子集,若对任意a,b∈A,有a⊕b∈A,则称A对运算⊕封闭.下列数集对加法、减法、乘法和除法(除数不等于零)四则运算都封闭的是( )
A.自然数集 B.整数集 C.有理数集 D.无理数集
9. △ABC的三内角A,B,C所对边的长分别为a,b,c,设向量p→=(a+c,b),q→=(b-a,c-a),若p→ // q→,则角C的大小为( )
A.π6 B.π3 C.π2 D.2π3
10. 已知等腰△ABC的腰为底的2倍,则顶角A的正切值是( )
A.32 B.3 C.158 D.157
11. 与函数y=e2x-2ex+1(x≥0)的曲线关于直线y=x对称的曲线的方程为( )
A.y=ln(1+x) B.y=ln(1-x) C.y=-ln(1+x) D.y=-ln(1-x)
12. 曲线x210-m+y26-m=1(m<6)与曲线x25-m+y29-m=1(5
0,则g(g(12))=________.
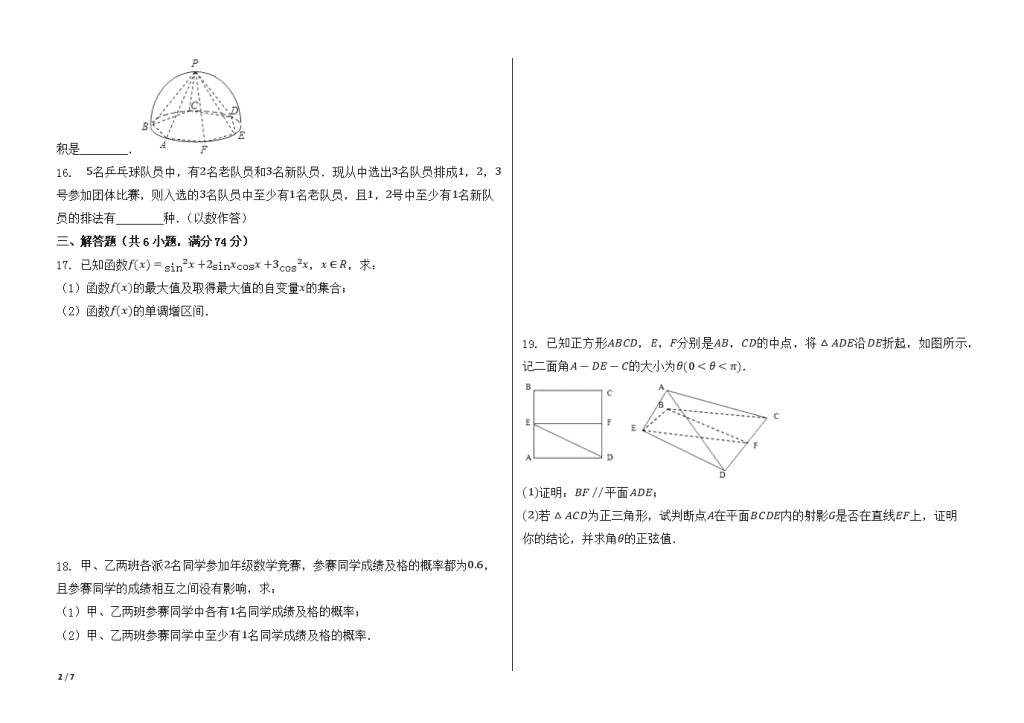
15. 如图,半径为2的半球内有一内接正六棱锥P-ABCDEF,则此正六棱锥的侧面积是
8 / 8
________.
16. 5名乒乓球队员中,有2名老队员和3名新队员.现从中选出3名队员排成1,2,3号参加团体比赛,则入选的3名队员中至少有1名老队员,且1,2号中至少有1名新队员的排法有________种.(以数作答)
三、解答题(共6小题,满分74分)
17. 已知函数f(x)=sin2x+2sinxcosx+3cos2x,x∈R,求:
(1)函数f(x)的最大值及取得最大值的自变量x的集合;
(2)函数f(x)的单调增区间.
18. 甲、乙两班各派2名同学参加年级数学竞赛,参赛同学成绩及格的概率都为0.6,且参赛同学的成绩相互之间没有影响,求:
(1)甲、乙两班参赛同学中各有1名同学成绩及格的概率;
(2)甲、乙两班参赛同学中至少有1名同学成绩及格的概率.
19. 已知正方形ABCD,E,F分别是AB,CD的中点,将△ADE沿DE折起,如图所示,记二面角A-DE-C的大小为θ(0<θ<π).
(1)证明:BF // 平面ADE;
(2)若△ACD为正三角形,试判断点A在平面BCDE内的射影G是否在直线EF上,证明你的结论,并求角θ的正弦值.
8 / 8
20. 已知等差数列{an}的前n项和为Sn=pn2-2n+q(p, q∈R),n∈N+.
(1)求的q值;
(2)若a1与a5的等差中项为18,bn满足an=2log2bn,求数列{bn}的前n和Tn.
21. 已知函数f(x)=13ax3+(a+d)x2+(a+2d)x+d,g(x)=ax2+2(a+2d)x+a+4d,其中a>0,d>0,设x0为f(x)的极小值点,x1为g(x)的极值点,g(x2)=g(x3)=0,并且x2<x3,将点(x0, f(x0)),(x1, g(x1),(x2, 0)(x3, 0)依次记为A,B,C,D.
(1)求x0的值;
(2)若四边形ABCD为梯形且面积为1,求a,d的值.
22. 已知点A(x1, y1),B(x2, y2)(x1x2≠0)是抛物线y2=2px(p>0)上的两个动点,O是坐标原点,向量OA→,OB→满足|OA→+OB→|=|OA→-OB→|,设圆C的方程为x2+y2-(x1+x2)x-(y1+y2)y=0.
(1)证明线段AB是圆C的直径;
(2)当圆C的圆心到直线x-2y=0的距离的最小值为255时,求p的值.
8 / 8
8 / 8
参考答案与试题解析
2006年辽宁省高考数学试卷(文科)
一、选择题(共12小题,每小题5分,满分60分)
1.D
2.C
3.D
4.B
5.A
6.D
7.A
8.C
9.B
10.D
11.A
12.A
二、填空题(共4小题,每小题4分,满分16分)
13.5
14.12
15.67
16.48
三、解答题(共6小题,满分74分)
17.解:(1)解法一:∵ f(x)=1-cos2x2+sin2x+3(1+cos2x)2=2+sin2x+cos2x=2+2sin(2x+π4)
∴ 当2x+π4=2kπ+π2,即x=kπ+π8(k∈Z)时,f(x)取得最大值2+2.
因此,f(x)取得最大值的自变量x的集合是{x|x=kπ+π8,k∈Z}.
解法二:∵ f(x)=(sin2x+cos2x)+sin2x+2cos2x=1+sin2x+1+cos2x=2+2sin(2x+π4)
∴ 当2x+π4=2kπ+π2,即x=kπ+π8(k∈Z)时,f(x)取得最大值2+2.
因此,f(x)取得最大值的自变量x的集合是{x|x=kπ+π8,k∈Z}
(2)解:f(x)=2+2sin(2x+π4)
由题意得2kπ-π2≤2x+π4≤2kπ+π2(k∈Z),即kπ-38π≤x≤kπ+π8(k∈Z).
因此,f(x)的单调增区间是[kπ-3π8,kπ+π8](k∈Z).
18.解:(1)∵ 甲班参赛同学恰有1名同学成绩及格的概率为C21×0.6×0.4=0.48
乙班参赛同学中恰有一名同学成绩及格的概率为C21×0.6×0.4=0.48
由于参赛同学的成绩相互之间没有影响,是相互独立的,
∴ 甲、乙两班参赛同学中各有1名同学成绩及格的概率为
P=0.48×0.48=0.2304
(2)解法一:甲、乙两班4名参赛同学成绩都不及格的概率为0.44=0.0256
故甲、乙两班参赛同学中至少有一名同学成绩都及格的概率为
P=1-0.0256=0.9744
解法二:甲、乙两班参赛同学有一人成绩及格的概率为C41×0.6×0.4=0.1536
甲、乙两班参赛同学中恰有2名同学成绩及格的概率为C42×0.62×0.42=0.3456
甲、乙两班参赛同学中恰有3名同学成绩及格的概率为C42×0.62×0.42=0.3456
甲、乙两班4同学参赛同学成绩都及格的概率为0.64=0.1296
故甲、乙两班参赛同学中至少有1名同学成绩及格的概率为
P=0.1536+0.3456+0.3456+0.1296=0.9744
19.(1)证明:E,F分别为正方形ABCD的边AB,CD的中点,
∵ EB // FD,且EB=FD,
∴ 四边形EBFD为平行四边形.
8 / 8
∴ BF // ED
∵ ED⊂平面AED,而BF⊄平面AED
∴ BF // 平面ADE.
(2)解:如图,点A在平面BCDE内的射影G在直线EF上,
过点A作AG垂直于平面BCDE,垂足为G,连接GC,GD.
∵ △ACD为正三角形,
∴ AC=AD.
∴ CG=GD.
∵ G在CD的垂直平分线上,
∴ 点A在平面BCDE内的射影G在直线EF上,
过G作GH垂直于ED于H,连接AH,则AH⊥DE,
所以∠AHG为二面角A-DE-C的平面角.
即∠AHG=θ.
设原正方体的边长为2a,连接AF.
在折后图的△AEF中,AF=3a,EF=2AE=2a,
即△AEF为直角三角形,AG⋅EF=AE⋅AF.
∴ AG=32a.
在Rt△ADE中,AH⋅DE=AE⋅AD.
∴ AH=25a.
∴ GH=a25.
cosθ=GHAH=14.
即sinθ=154.
20.解:(1)当n=1时,a1=S1=p-2+q
当n≥2时,an=Sn-Sn-1=pn2-2n+q-p(n-1)2+2(n-1)-q=2pn-p-2
∵ {an}是等差数列,a1符合n≥2时,an的形式,
∴ p-2+q=2p-p-2,
∴ q=0
(2)∵ a3=a1+a52,由题意得a3=18
又a3=6p-p-2,∴ 6p-p-2=18,解得p=4
∴ an=8n-6
由an=2log2bn,得bn=24n-3.
∴ b1=2,bn+1bn=24(n+1)-324n-3=24=16,即{bn}是首项为2,公比为16的等比数列
∴ 数列{bn}的前n项和Tn=2(1-16n)1-16=215(16n-1).
21.解:(1)f'(x)=ax2+2(a+d)x+a+2d=(x+1)(ax+a+2d),
令f'(x)=0,
由a≠0得x=-1或x=-1-2da
∵ a>0,d>0.
∴ -1-2da<-1
当-1-2da-1时f'(x)>0,
所以f(x)在x=-1处取极小值,即x0=-1
(2)解:g(x)=ax2+(2a+4d)x+a+4d
∵ a>0,x∈R
8 / 8
∴ g(x)在x=-2a+4d2a=-1-2da处取得极小值,即x1=-1-2da,
由g(x)=0,即(ax+a+4d)(x+1)=0,
∵ a>0,d>0,x2<x3,
∴ x3=-1,x2=-1-4da,
∵ f(x0)=f(-1)=-13a
g(x1)=g(-1-2da)=-4d2a
∴ A(-1,-13a),B(-1-2da,-4d2a),C(-1-4da,0),D(-1, 0)
由四边形ABCD是梯形及BC与AD不平行,得AB // CD.
-a3=-4d2a即a2=12d2
由四边形ABCD的面积为1,得12(|AB|+|CD|)⋅|AD|=1
即12(4da+2da)⋅a3=1得d=1,
从而a2=12得a=23,d=1
22.解:(1)∵ 向量OA→,OB→满足|OA→+OB→|=|OA→-OB→|,
∴ (OA→+OB→)2=(OA→-OB→)2
即OA→2+2OA→⋅OB→+OB→2=OA→2-2OA→⋅OB→+OB→2
整理得OA→⋅OB→=0
∵ 点A(x1, y1),B(x2, y2)
∴ OA→=(x1, y1),OB→=(x2, y2)
∴ x1x2+y1y2=0①
设点M(x, y)是以线段AB为直径的圆上的任意一点,
则MA→⋅MB→=0
即(x-x1)(x-x2)+(y-y1)(y-y2)=0
展开上式并将 ①代入得x2+y2-(x1+x2)x-(y1+y2)y=0
故线段AB是圆C的直径.
(II)设圆C的圆心为C(x, y),
则x=x1+x22,y=y1+y22
∵ y12=2px1,y22=2px2(p>0),
∴ x1x2=y12y224p2
又∵ x1x2+y1y2=0
∴ x1x2=-y1y2
∴ -y1y2=y12y224p2
∴ y1y2=-4p2
∴ x=x1+x22=14p(y12+y22)
=14p(y12+y22+2y1y2)-y1y22p
=1p(y2+2p2)
∴ 圆心的轨迹方程为:y2=px-2p2
设圆心C到直线x-2y=0的距离为d,则
d=|x-2y|5
=|1p(y2+2p2)-2y|5
=|(y-p)2+p2|5p
当y=p时,d有最小值p5,
由题设得p5=255
8 / 8
∴ p=2
8 / 8