- 2021-04-12 发布 |
- 37.5 KB |
- 12页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高考数学模拟试卷 (18)
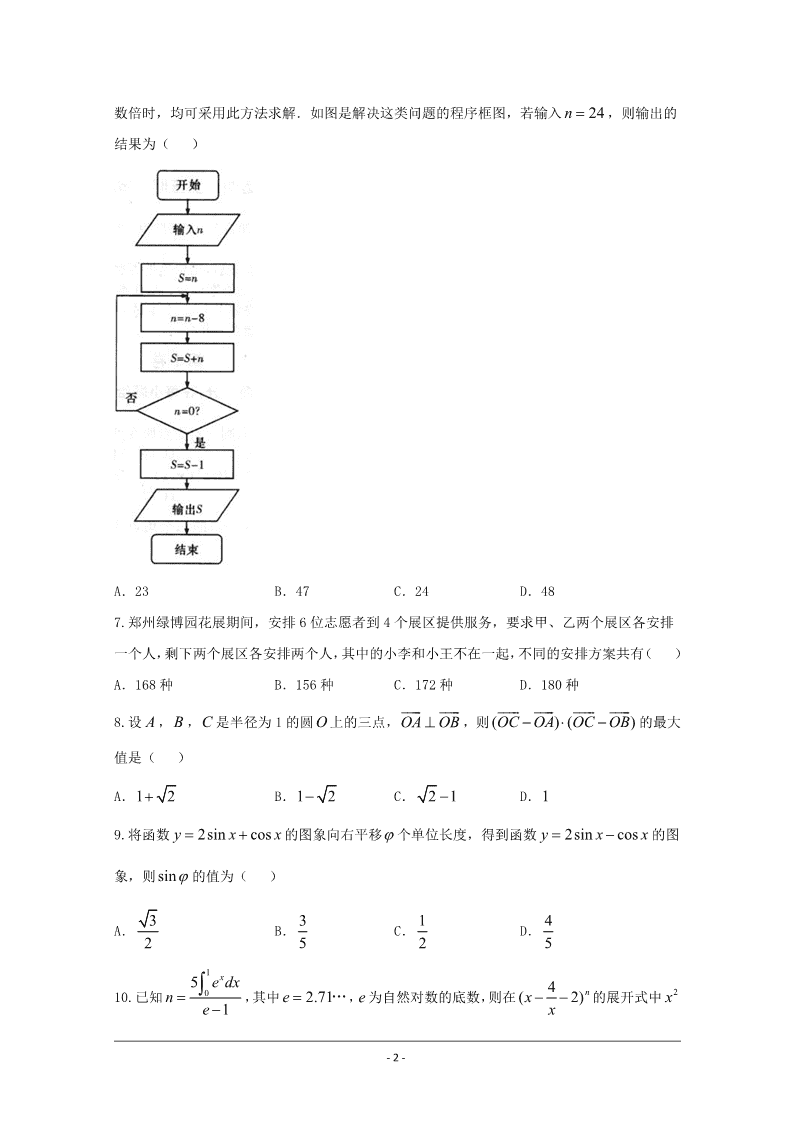
- 1 - 长沙市雅礼中学、河南省实验中学 2018 届高三联合考试试题 数学(理科)(18) 第Ⅰ卷(共 60 分) 一、选择题:本大题共 12 个小题,每小题 5 分,共 60 分.在每小题给出的四个选项中,只有一 项是符合题目要求的. 1.已知复数 z 满足 | | 3z z i ,则 z 对应点所在的象限是( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限 2.设集合 2 2( , ) | 1A x y x y , ( , ) | 3xB x y y ,则 A B 的子集的个数是( ) A.4 B.3 C.2 D.1 3.已知双曲线 2 2 2 2 1y x a b ( 0a , 0b )的一个焦点为 (0, 2)F ,一条渐近线的斜率为 3 , 则该双曲线的方程为( ) A. 2 2 13 x y B. 2 2 13 yx C. 2 2 13 y x D. 2 2 13 xy 4.在数列 na 中, 1 2a , 1 1ln(1 )1 n na a n n n ,则 na ( ) A. 2 lnn n B. 2 ( 1)lnn n n C. 2 lnn n n D.1 lnn n n 5.某几何体的三视图如图所示,其中正视图由矩形和等腰直角三角形组成,侧视图由半圆和 等腰直角三角形组成,俯视图的实线部分为正方形,则该几何体的表面积为( ) A.3 4 2 B. 4( 2 1) C. 4( 2) D. 4( 1) 6.《孙子算经》是中国古代重要的数学著作,书中有一问题:“今有方物一束,外周一匝有三 十二枚,问积几何?”该著作中提出了一种解决此问题的方法:“重置二位,左位减八,余加 右位,至尽虚减一,即得.”通过对该题的研究发现,若一束方物外周一匝的枚数 n 是 8 的整 - 2 - 数倍时,均可采用此方法求解.如图是解决这类问题的程序框图,若输入 24n ,则输出的 结果为( ) A.23 B.47 C.24 D.48 7.郑州绿博园花展期间,安排 6 位志愿者到 4 个展区提供服务,要求甲、乙两个展区各安排 一个人,剩下两个展区各安排两个人,其中的小李和小王不在一起,不同的安排方案共有( ) A.168 种 B.156 种 C.172 种 D.180 种 8.设 A ,B ,C 是半径为 1 的圆 O 上的三点,OA OB ,则 ( ) ( )OC OA OC OB 的最大 值是( ) A.1 2 B.1 2 C. 2 1 D.1 9.将函数 2sin cosy x x 的图象向右平移 个单位长度,得到函数 2sin cosy x x 的图 象,则sin 的值为( ) A. 3 2 B. 3 5 C. 1 2 D. 4 5 10.已知 1 0 5 1 xe dx n e ,其中 2.71e …,e 为自然对数的底数,则在 4( 2)nx x 的展开式中 2x - 3 - 的系数是( ) A.240 B.80 C. 80 D. 240 11.过抛物线C : 2 4y x 的焦点 F 的直线l 与抛物线 C 交于 P ,Q 两点,与抛物线准线交于 M ,且 3FM FP ,则| |FP ( ) A. 3 2 B. 2 3 C. 4 3 D. 3 4 12.已知函数 ( ) sin 2f x x 的图象与直线 2 2 0kx y k ( 0k )恰有三个公共点,这三 个点的横坐标从小到大分别为 1x , 2x , 3x ,则 1 3 2 3( ) tan( 2 )x x x x ( ) A. 2 B. 1 C. 0 D.1 第Ⅱ卷(共 90 分) 二、填空题(每题 5 分,满分 20 分,将答案填在答题纸上) 13.已知实数 x , y 满足 1, 1, 0, x y x y x 则 2 2x y x 的最小值为 . 14.已知点 ( , )P a b 在函数 2ey x (其中 2.71e …,e 为自然对数的底数)的图象上,且 1a , 1b ,则 lnba 的最大值为 . 15.现为一球状巧克力设计圆锥体的包装盒,若该巧克力球的半径为 3,则其包装盒的体积的 最小值为 . 16.在平面四边形 ABCD 中, 120ABC , 2 19AC , 2 3AB BC , 2AD BD , BCD 的面积为 2 3 ,则 AD . 三、解答题 (本大题共 6 小题,共 70 分.解答应写出文字说明、证明过程或演算步骤.) 17.若数列 na 的前 n 项和 nS 满足 2n nS a ( 0 , *n N ). (1)证明:数列 na 为等比数列,并求 na ; (2)若 4 , 2 , , log , n n n a nb a n 是奇 是偶 ( *n N ),求数列 nb 的前 n 项和 nT . 18.如图 1,菱形 ABCD 的边长为 12, 60BAD , AC 与 BD 交于O 点,将菱形 ABCD - 4 - 沿对角线 AC 折起,得到三棱锥 B ACD ,点 M 是棱 BC 的中点, 6 2DM . (1)求证:平面ODM 平面 ABC ; (2)求二面角 M AD C 的余弦值. 19.某基地蔬菜大棚采用水培、无土栽培方式种植各类蔬菜.过去 50 周的资料显示,该地周 光照量 X (小时)都在 30 小时以上,其中不足 50 小时的周数有 5 周,不低于 50 小时且不超 过 70 小时的周数有 35 周,超过 70 小时的周数有 10 周.根据统计,该基地的西红柿增加量 y (百斤)与使用某种液体肥料 x (千克)之间对应数据为如图所示的折线图. (1)依据数据的折线图,是否可用线性回归模型拟合 y 与 x 的关系?请计算相关系数 r 并加 以说明(精确到 0.01);(若| | 0.75r ,则线性相关程度很高,可用线性回归模型拟合) (2)蔬菜大棚对光照要求较大,某光照控制仪商家为该基地提供了部分光照控制仪,但每周 光照控制仪最多可运行台数受周光照量 X 限制,并有如表关系: 若某台光照控制仪运行,则该台光照控制仪周利润为 3000 元;若某台光照控制仪未运行,则 该台光照控制仪周亏损 1000 元.以过去 50 周的周光照量的频率作为周光照量发生的概率, 商家欲使周总利润的均值达到最大,应安装光照控制仪多少台? 附:相关系数公式 1 2 2 1 1 ( )( ) ( ) ( ) n i i i n n i i i i x x y y r x x y y ,参考数据 0.3 0.55 , 0.9 0.95 . - 5 - 20.设点 A 为圆C : 2 2 4x y 上的动点,点 A 在 x 轴上的投影为Q ,动点 M 满足 2MQ AQ ,动点 M 的轨迹为 E . (1)求 E 的方程; (2)设 E 与 y 轴正半轴的交点为 B ,过点 B 的直线l 的斜率为 k ( 0k ),l 与 E 交于另一 点为 P ,若以点 B 为圆心,以线段 BP 长为半径的圆与 E 有 4 个公共点,求 k 的取值范围. 21.已知函数 2( ) x x xf x ae ae xe ( 0a , 2.718e …, e 为自然对数的底数),若 ( ) 0f x 对于 x R 恒成立. (1)求实数 a 的值; (2)证明: ( )f x 存在唯一极值点 0x ,且 02 ln 2 1 1( )2 4 4f xe e . 请考生在 22、23 两题中任选一题作答,如果多做,则按所做的第一题记分. 22.选修 4-4:坐标系与参数方程 在平面直角坐标系 xOy 中,倾斜角为 的直线l 过点 ( 2, 4)M ,以原点 O 为极点, x 轴的 正半轴为极轴,建立极坐标系,曲线 C 的极坐标方程为 2sin 2cos . (1)写出直线l 的参数方程( 为常数)和曲线C 的直角坐标方程; (2)若直线l 与C 交于 A 、 B 两点,且| | | | 40MA MB ,求倾斜角 的值. 23.选修 4-5:不等式选讲 已知函数 ( ) | 1| | 1|f x m x x . (1)当 5m 时,求不等式 ( ) 2f x 的解集; (2)若二次函数 2 2 3y x x 与函数 ( )y f x 的图象恒有公共点,求实数 m 的取值范围. - 6 - 长沙市雅礼中学、河南省实验中学 2018 届高三联合考试试题数学(理科)答案(18) 一、选择题 1-5: DACCA 6-10: BBADB 11、12:CB 二、填空题 13.4 14. e 15.72 16. 4 3 三、解答题 17.解:(1)由题意可知 1 12S a ,即 1a ; 当 2n 时, 1 1 1(2 ) (2 ) 2 2n n n n n n na S S a a a a ,即 12n na a ; 所以数列 na 是首项为 ,公比为 2 的等比数列, 所以 12n na . (2)由(1)可知当 4 时 12n na ,从而 12 , 1, n n nb n n 是奇, 是偶. n 为偶数时, 2 (3 1)4(1 4 ) 2 1 4 2 n n n n T ; n 为奇数时, 1 1n n nT T b 1 2 1(3 1 1)4(1 4 ) 2 ( 2)1 4 2 n n n n 14(2 1) ( 1)( 5) 23 4 n n n n 14(2 1) ( 1)( 3) 3 4 n n n , 综上, 1 4(2 1) ( 4) ,3 4 4(2 1) ( 1)( 3) ,3 4 n n n n n n T n n n 是偶, 是奇. 18.(1)证明:∵四边形 ABCD 是菱形, ∴ AD DC ,OD AC , ADC 中, 12AD DC , 120ADC , ∴ 6OD , - 7 - 又 M 是 BC 中点,∴ 1 62OM AB ,又 6 2MD , ∵ 2 2 2OD OM MD ,∴ DO OM , ∵OM , AC 平面 ABC ,OM AC O , ∴OD 平面 ABC , 又∵OD 平面ODM ,∴平面ODM 平面 ABC . (2)解:由题意,OD DC ,OB OC , 又由(1)知OB OD ,建立如图所示空间直角坐标系,由条件知: (6,0,0)D , (0, 6 3,0)A , (0,3 3,3)M , 故 (0,9 3,3)AM , (6,6 3,0)AD , 设平面 MAD 的法向量 ( , , )m x y z , 则 0, 0, m AM m AD 即 9 3 3 0, 6 6 3 0, y z x y 令 3y ,则 3x , 9z , ∴ (3, 3,9)m . 由条件知 OB 平面 ACD ,故取平面 ACD 的法向量为 (0,0,1)n , 所以, 3 93cos , 31| | | | m nm n m n , 由图知二面角 M AD C 为锐二面角, 故二面角 M AD C 的余弦值为 3 93 31 . 19.解:(1)由已知数据可得 2 4 5 6 8 55x , 3 4 4 4 5 45y , 因为 5 1 ( )( ) ( 3) ( 1) 0 0 0 3 1 6i i i x x y y , 5 2 2 2 2 2 2 1 ( ) ( 3) ( 1) 0 1 3 2 5i i x x , 5 2 2 2 2 2 2 1 ( ) ( 1) 0 0 0 1 2i j y y , - 8 - 所以相关系数 1 2 2 1 1 ( )( ) ( ) ( ) n i i i n n i i i j x x y y r x x y y 6 9 0.95102 5 2 , 因为 0.75r ,所以可用线性回归模型拟合 y 与 x 的关系. (2)记商家周总利润为Y 元,由条件可知至少需要安装 1 台,最多安装 3 台光照控制仪. ①安装 1 台光照控制仪可获得周总利润 3000 元; ②安装 2 台光照控制仪的情形: 当 70X 时,只有 1 台光照控制仪运行,此时周总利润 3000 1000 2000Y 元, 当30 70X 时,2 台光照控制仪都运行,此时周总利润 2 3000 6000Y 元, 故Y 的分布列为: Y 2000 6000 P 0.2 0.8 所以 ( ) 1000 0.2 5000 0.7 9000 0.1 4600E Y 元. 综上可知,为使商家周利润的均值达到最大应该安装 2 台光照控制仪. 20.解:(1)设点 ( , )M x y ,由 2MQ AQ ,得 ( ,2 )A x y , 由于点 A 在圆C : 2 2 4x y 上,则 2 24 4x y , 即点 M 的轨迹 E 的方程为 2 2 14 x y . (2)由(1)知, E 的方程为 2 2 14 x y , 因为 E 与 y 轴的正半轴的交点为 B ,所以 (0,1)B , 所以故 B 且斜率为 k 的直线l 的方程为 1y kx ( 0k ). 由 2 2 1, 1,4 y kx x y 得 2 2(1 4 ) 8 0k x kx , 设 1 1( , )B x y , 2 2( , )P x y ,因此 1 0x , 2 2 8 1 4 kx k , 2 2 1 2 2 8| || | 1 | | 11 4 kBP k x x kk . - 9 - 由于圆与椭圆的公共点有4个,由对称性可设在 y 轴左侧的椭圆上有两个不同的公共点 P ,T , 满足| | | |BP BP ,此时直线 BP 斜率 0k , 设直线 BT 的斜率为 1k ,且 1 0k , 1k k , 则 21 12 1 8| || | 11 4 kBT kk , 故 2 21 12 2 1 8| | 8| |1 11 4 1 4 k kk kk k ,所以 2 4 2 4 1 1 2 2 1 01 4 1 4 k k k k k k , 即 2 2 4 2 2 4 1 1 1(1 4 ) (1 4 )k k k k k k , 所以 2 2 2 2 2 2 1 1 1( )(1 8 ) 0k k k k k k , 由于 1 2k k ,因此 2 2 2 2 1 11 8 0k k k k , 故 2 2 1 2 2 1 1 1 1 9 8 1 8 8(8 1) kk k k . 因为 2 0k ,所以 2 18 1 0k , 因此 2 2 1 1 9 1 8 8(8 1) 8k k ,又因为 0k ,所以 2 4k , 又因为 1k k ,所以 2 2 2 21 8 0k k k k , 所以 4 28 2 1 0k k ,又因为 0k ,解得 2 2k , 所以 2 2 2( , ) ( , )4 2 2k , 综上所述, k 的取值范围为 2 2 2 2 2 2( , ) ( , ) ( , ) ( , )2 2 4 4 2 2 . - 10 - 21.解:(1)由 ( ) ( ) 0x xf x e ae a x ,可得 ( ) 0xg x ae a x , 因为 (0) 0g ,所以 ( ) (0)g x g , 从而 0x 是 ( )g x 的一个极小值点, 由于 '( ) 1xg x ae ,所以 '(0) 1 0g a ,即 1a . 当 1a 时, ( ) 1xg x e x , '( ) 1xg x e , ∵ ( ,0)x 时, '( ) 0g x , ( )g x 在 ( ,0) 上单调递减, (0, )x 时, '( ) 0g x , ( )g x 在 (0, ) 上单调递增; ∴ ( ) (0) 0g x g ,故 1a . (2)当 1a 时, 2( ) x x xf x e e xe , '( ) (2 2)x xf x e e x . 令 ( ) 2 2xh x e x ,则 '( ) 2 1xh x e , ∵ ( , ln 2)x 时, '( ) 0h x , ( )h x 在 ( , ln 2) 上为减函数; ( ln 2, )x 时, '( ) 0h x , ( )h x 在 ( ln 2, ) 上为增函数, 由于 ( 1) 0h , ( 2) 0h ,所以在 ( 2, 1) 上存在 0x x 满足 0( ) 0h x , ∵ ( )h x 在 ( , ln 2) 上为减函数, ∴ 0( , )x x 时, ( ) 0h x ,即 '( ) 0f x , ( )f x 在 0( , )x 上为增函数, 0( , ln 2)x x 时, ( ) 0h x ,即 '( ) 0f x , ( )f x 在 0( , ln 2)x 上为减函数, ( ln 2,0)x 时, ( ) 0h x ,即 '( ) 0f x , ( )f x 在 ( ln 2,0) 上为减函数, - 11 - (0, )x 时, ( ) 0h x ,即 '( ) 0f x , ( )f x 在 (0, ) 上为增函数, 因此 ( )f x 在 ( ln 2, ) 上只有一个极小值点 0, 综上可知, ( )f x 存在唯一的极大值点 0x ,且 0 ( 2, 1)x . ∵ 0( ) 0h x ,∴ 0 02 2 0xe x , 所以 0 0 0 2 2 20 0 0 0 0 0 0 2 2 2( ) ( ) ( )( 1)2 2 4 x x x x x x xf x e e x e x , 0 ( 2, 1)x , ∵ ( 2, 1)x 时, 2 2 1 4 4 x x ,∴ 0 1( ) 4f x ; ∵ 1ln ( 2, 1)2e ,∴ 0 2 1 ln 2 1( ) (ln )2 2 4f x f e e e ; 综上知: 02 ln 2 1 1( )2 4 4f xe e . 22.解:(1)∵倾斜角为 的直线过点 ( 2, 4)M , ∴直线l 的参数方程是 2 cos , 4 sin x t y t (t 是参数), ∵曲线C 的极坐标方程为 2sin 2cos ,∴曲线C 的直角坐标方程是: 2 2y x . (2)把直线的参数方程代入 2 2y x ,得 2 2sin (2cos 8sin ) 20 0t t , ∴ 1 2 2 2cos 8sin sint t , 1 2 2 20 sint t , 根据直线参数方程的几何意义 1 2 2 20| || | | | 40sinMA MB t t ,故 4 或 3 4 , 又∵ 2 2(2cos 8sin ) 80sin 0 , ∴ 3 4 . 23.解:(1)当 5m 时, 5 2 , 1, ( ) 3, 1 1, 5 2 , 1. x x f x x x x 由 ( ) 2f x 得不等式的解集为 3 3| 2 2x x . - 12 - (2)由二次函数 2 22 3 ( 1) 2y x x x ,该函数在 1x 取得最小值 2, 因为 2 , 1, ( ) 2, 1 1, 2 , 1, m x x f x m x m x x 在 1x 处取得最大值 2m , 所以要使二次函数 2 2 3y x x 与函数 ( )y f x 的图象恒有公共点, 只需 2 2m ,即 4m .查看更多