2010年贵州省安顺市中考数学试卷

2010年贵州省安顺市中考数学试卷

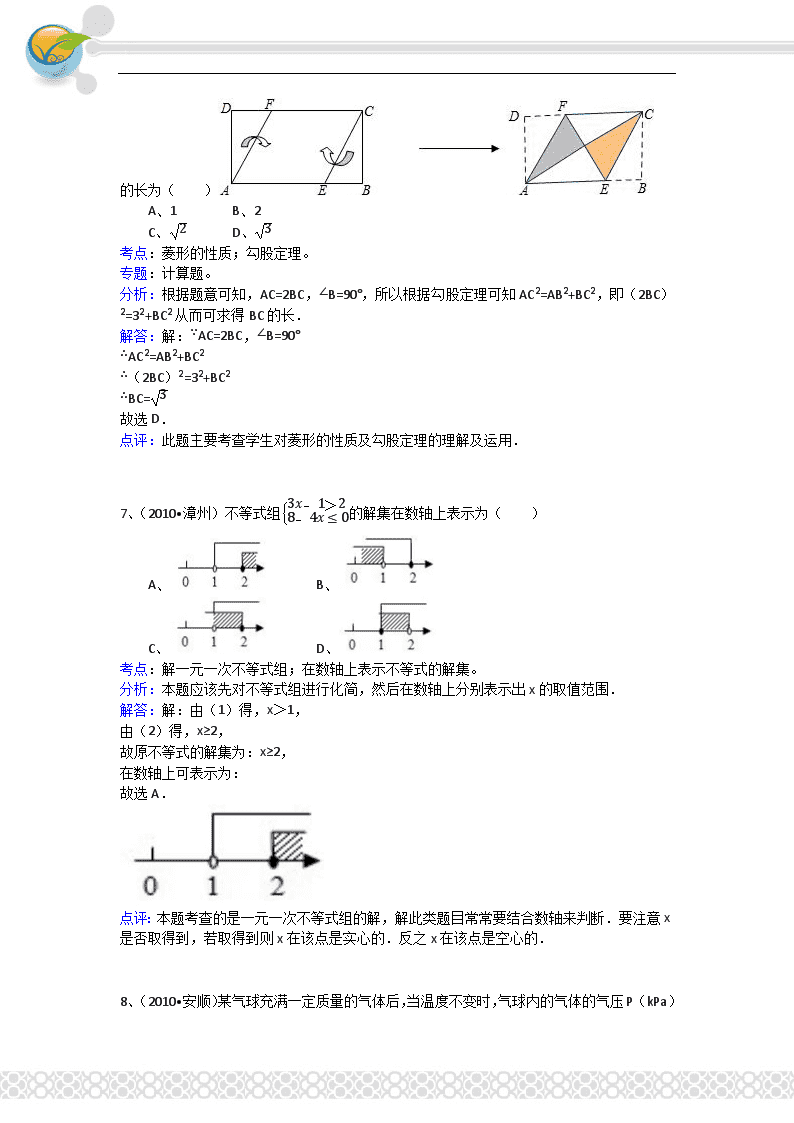
一、选择题（共10小题，每小题3分，满分30分）‎ ‎1、（2010•安顺）台湾是我国最大的岛屿，总面积为35989.76平方千米．用科学记数法应表示为（保留三个有效数字）（　　）‎ ‎ A、3.59×106平方千米 B、3.60×106平方千米 ‎ C、3.59×104平方千米 D、3.60×104平方千米 考点：科学记数法与有效数字。‎ 专题：应用题。‎ 分析：科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值大于10时，n是正数；当原数的绝对值小于1时，n是负数．‎ 有效数字是从左边第一个不是0的数字起后面所有的数字都是有效数字．用科学记数法表示的数的有效数字只与前面的a有关，与10的多少次方无关．‎ 解答：解：35 989.76=3.598976×104≈3.60×104平方千米．‎ 故选D．‎ 点评：本题考查了科学记数法、有效数字两个概念．科学记数法是指把一个数写成a×10n（其中1≤|a|＜10，n是整数）的形式．本题中10的指数就是原数的整数位数减去1．有效数字则是左边第一个不是0的数起到精确到的位数止，只与a有关，取舍时要注意遵循四舍五入的原则．‎ ‎2、（2010•安顺）为了解国家提倡的“阳光体育运动”的实施情况，将某校中的40名学生一周的体育锻炼时间绘制成了如图所示的条形统计图，根据统计图提供的数据，该校40名同学一周参加体育锻炼时间的众数与中位数分别是（　　）‎ ‎ A、8，9 B、8，8‎ ‎ C、9，8 D、10，9‎ 考点：中位数；条形统计图；众数。‎ 专题：图表型。‎ 分析：众数是在一组数据中出现次数最多的数据，中位数是将一组数据按大小依次排列，把处在最中间位置的一个数据或者最中间两个数据的平均数叫这组数据的中位数．本组数据中，8出现了16次，出现的次数最多．把数据按照从大到小的顺序排列，最中间的两个数是的平均数即为中位数．‎ 解答：解：由条形统计图中出现频数最大条形最高的数据是在第二组，故众数是8（小时）；因图中是按从小到大的顺序排列的，最中间的年龄是9（小时），故中位数是9（小时）．‎ 故选A．‎ 点评：本题考查的是众数和中位数的定义．要注意，当所给数据有单位时，所求得的众数和中位数与原数据的单位相同，不要漏单位．‎ ‎3、（2010•安顺）下列关于‎12‎的说法中错误的是（　　）‎ ‎ A、‎12‎是无理数 B、3＜‎12‎＜4‎ ‎ C、‎12‎是12的算术平方根 D、‎12‎不能再化简 考点：二次根式的乘除法。‎ 分析：根据化简二次根式的法则可知．‎ 解答：解：因为‎12‎=2‎3‎，‎ 所以‎12‎能再化简．‎ 故选D．‎ 点评：化简二次根式，关键是看被开方数有没有能开得尽方的因数和因式．‎ ‎4、（2010•安顺）小华拿一个矩形木框在阳光下玩，矩形木框在地面上形成的投影不可能的是（　　）‎ ‎ A、 B、‎ ‎ C、 D、‎ 考点：平行投影。‎ 分析：在不同时刻，同一物体的影子的方向和大小可能不同，不同时刻物体在太阳光下的影子的大小在变，方向也在改变，依此进行分析．‎ 解答：解：矩形木框在地面上形成的投影应是平行四边形或一条线段，‎ 即相对的边平行或重合，‎ 故A不可能，即不会是梯形．‎ 故选A．‎ 点评：本题考查了平行投影特点，不同位置，不同时间，影子的大小、形状可能不同，具体形状应视其外在形状，及其与光线的夹角而定．‎ ‎5、（2010•安顺）为了调查某一路口某时段的汽车流量，记录了15天同一时段通过该路口的汽车辆数，其中有2天是142辆，2天是145辆，6天是156辆，5天是157辆，那么这15天通过该路口汽车平均辆数为（　　）‎ ‎ A、146 B、150‎ ‎ C、153 D、1600‎ 考点：加权平均数。‎ 分析：本题可先求出15天内经过的总的车辆数，再除以15即可．‎ 解答：解：依题意有：（142×2+145×2+6×156+5×157）÷15=153．‎ 故选C．‎ 点评：本题考查的是加权平均数的求法，总数除以数据的个数等于平均数．‎ ‎6、（2010•安顺）将矩形纸片ABCD按如图所示的方式折叠，得到菱形AECF．若AB=3，则BC 的长为（　　）‎ ‎ A、1 B、2‎ ‎ C、‎2‎ D、‎‎3‎ 考点：菱形的性质；勾股定理。‎ 专题：计算题。‎ 分析：根据题意可知，AC=2BC，∠B=90°，所以根据勾股定理可知AC2=AB2+BC2，即（2BC）2=32+BC2从而可求得BC的长．‎ 解答：解：∵AC=2BC，∠B=90°‎ ‎∴AC2=AB2+BC2‎ ‎∴（2BC）2=32+BC2‎ ‎∴BC=‎‎3‎ 故选D．‎ 点评：此题主要考查学生对菱形的性质及勾股定理的理解及运用．‎ ‎7、（2010•漳州）不等式组‎&3x﹣1＞2‎‎&8﹣4x≤0‎的解集在数轴上表示为（　　）‎ ‎ A、 B、‎ ‎ C、 D、‎ 考点：解一元一次不等式组；在数轴上表示不等式的解集。‎ 分析：本题应该先对不等式组进行化简，然后在数轴上分别表示出x的取值范围．‎ 解答：解：由（1）得，x＞1，‎ 由（2）得，x≥2，‎ 故原不等式的解集为：x≥2，‎ 在数轴上可表示为：‎ 故选A．‎ 点评：本题考查的是一元一次不等式组的解，解此类题目常常要结合数轴来判断．要注意x是否取得到，若取得到则x在该点是实心的．反之x在该点是空心的．‎ ‎8、（2010•安顺）某气球充满一定质量的气体后，当温度不变时，气球内的气体的气压P（kPa ‎）是气体体积V（m3）的反比例函数，其图象如图所示，当气球内的气压大于140kPa时，气球将爆炸，为了安全起见，气体体积应（　　）‎ ‎ A、不大于‎24‎‎35‎m3 B、不小于‎24‎‎35‎m3‎ ‎ C、不大于‎24‎‎37‎m3 D、不小于‎24‎‎37‎m3‎ 考点：反比例函数的应用。‎ 专题：应用题。‎ 分析：根据题意有：当温度不变时，气球内的气体的气压P是气体体积V的反比例函数，其图象过点（0.8，120），故可求其解析式；故当气球内的气压不大于140kPa时，气体体积应不小于‎24‎‎35‎m3．‎ 解答：解：设球内气体的气压P（kPa）和气体体积V（m3）的关系式为P=kV，‎ ‎∵图象过（0.8，120）‎ ‎∴P=‎120×0.8‎V=‎96‎V，‎ ‎∴当P≤140kPa时，V≥‎24‎‎35‎m3，‎ 故选B．‎ 点评：现实生活中存在大量成反比例函数的两个变量，解答该类问题的关键是确定两个变量之间的函数关系．然后再根据题意确定变量的取值范围．‎ ‎9、（2010•安顺）如图，正方形ABCD中，E是BC边上一点，以E为圆心、EC为半径的半圆与以A为圆心，AB为半径的圆弧外切，则sin∠EAB的值为（　　）‎ ‎ A、‎4‎‎3‎ B、‎‎3‎‎4‎ ‎ C、‎4‎‎5‎ D、‎‎3‎‎5‎ 考点：相切两圆的性质；锐角三角函数的定义。‎ 分析：‎ 两圆相外切，则圆心距等于两圆半径的和．利用勾股定理和锐角三角函数的定义求解．‎ 解答：解：设正方形的边长为y，EC=x，‎ 由题意知，AE2=AB2+BE2，‎ 即（y+x）2=y2+（y﹣x）2，‎ 化简得，y=4x，‎ ‎∴sin∠EAB=BEAE=‎3‎‎5‎．‎ 故选D．‎ 点评：本题综合性较强，要把有关圆的知识联系起来使用．‎ ‎10、（2010•安顺）四个电子宠物排座位，一开始，小鼠、小猴、小兔、小猫分别坐在1，2，3，4号座位上（如图所示），以后它们不停地变换位置，第一次上下两排交换，第二次是在第一次换位后，再左右两列交换位置，第三次再上下两排交换，第四次再左右两列交换…这样一直下去，则第2005次交换位置后，小兔所在的号位是 ‎（　　）‎ ‎ A、1 B、2‎ ‎ C、3 D、4‎ 考点：规律型：数字的变化类。‎ 专题：规律型。‎ 分析：不难发现：小兔所在的号位的规律是4个一循环．‎ 解答：解：因为2005÷4=501…1，即第2005次交换位置后，小兔所在的号位应和第一次交换后的位置相同，即图1．‎ 故选C．‎ 点评：能够发现小兔所在的号位的规律是4个一循环，然后进行计算．‎ 二、填空题（共8小题，每小题4分，满分32分）‎ ‎11、（2010•安顺）将x﹣x2+‎1‎‎4‎x3分解因式的结果为 ．‎ 考点：提公因式法与公式法的综合运用。‎ 分析：先提取公因式x，然后再利用完全平方公式继续分解因式．‎ 解答：解：x﹣x2+‎1‎‎4‎x3，‎ ‎=x（‎1‎‎4‎x2﹣x+1），‎ ‎=x（‎1‎‎2‎x﹣1）2．‎ 故答案为：x（‎1‎‎2‎x﹣1）2．‎ 点评：本题考查了提公因式法和公式法分解因式，本题关键在于提取公因式后还可以继续进行二次因式分解，分解因式要彻底，直到不能再分解为止．‎ ‎12、（2010•安顺）如图，平行四边形ABCD中，E是边BC上的点，AE交BD于点F，如果BE=2EC，那么S△BEF：S△DAF= ．‎ 考点：相似三角形的判定与性质；平行四边形的性质。‎ 分析：已知BE=2EC，由平行四边形的对边相等即可求得BE、AD的比例关系；易证得△ADF∽△EBF，则BE、AD的比例关系即为两个三角形的相似比，根据相似三角形的面积比等于相似比的平方即可得解．‎ 解答：解：∵四边形ABCD是平行四边形，‎ ‎∴AD∥BC①，AD=BC②；‎ 已知BE=2EC，即BE：BC=2：3，由②可得BE：AD=2：3；‎ 由①知：△ADF∽△EBF，‎ ‎∴S△BEF：S△DAF=BE2：AD2=4：9．‎ 点评：此题主要考查了平行四边形和相似三角形的性质；相似三角形的对应边的比等于相似比，面积比等于相似比的平方．‎ ‎13、（2010•安顺）已知：如图，等腰三角形ABC中，AB=AC=4，若以AB为直径的⊙O与BC相交于点D，DE∥AB，DE与AC相交于点E，则DE= ．‎ 考点：圆周角定理；平行线的性质；等腰三角形的性质。‎ 专题：计算题。‎ 分析：作出辅助线，根据半圆或直径所对的圆周角为90°，判断出D为BC的中点，进而判断出DE为△ABC的中位线，根据中位线定理即可解答．‎ 解答：解：连接AD，‎ ‎∵AB为直径，‎ ‎∴∠ADB=90°，‎ 又∵AB=AC，‎ ‎∴D为BC的中点，‎ 又∵DE∥AB，‎ ‎∴DE为△ABC的中位线，‎ ‎∴DE=‎1‎‎2‎AB=‎1‎‎2‎×4=2．‎ 点评：本题重点考查了直径所对的圆周角为直角和中位线定理．‎ ‎14、（2010•安顺）在平面直角坐标系中，Rt△OAB的顶点A的坐标为‎（‎3‎，1）‎，若将△OAB绕O点，逆时针旋转60°后，B点到达B′点，则点B′的坐标是 ．‎ 考点：坐标与图形变化-旋转。‎ 分析：根据A点坐标可知∠AOB=30°，因此旋转后OA在y轴上．如图所示．作B′C′⊥y轴于C′点，运用三角函数求出B′C′、OC′的长度即可确定B′的坐标．‎ 解答：解：将△OAB绕O点，逆时针旋转60°后，位置如图所示，‎ 作B′C′⊥y轴于C′点，‎ ‎∵A的坐标为‎（‎3‎，1）‎，‎ ‎∴OB=‎3‎，AB=1，∠AOB=30°，‎ ‎∴OB′=‎3‎，∠B′OC′=30°，‎ ‎∴B′C′=‎3‎‎2‎，OC′=‎3‎‎2‎，‎ ‎∴B′（‎3‎‎2‎，‎3‎‎2‎）．‎ 点评：本题涉及图形旋转，体现了新课标的精神，抓住旋转的三要素：旋转中心O，旋转方向逆时针，旋转角度60°，通过画图计算得B′坐标．‎ ‎15、（2010•安顺）制作一个圆锥模型，已知圆锥底面圆的半径为3.5cm，侧面母线长为6cm，则此圆锥侧面展开图的扇形圆心角为 度．‎ 考点：弧长的计算。‎ 分析：利用圆锥侧面展开扇形圆心角与母线和底面圆半径的关系计算．‎ 解答：解：圆锥底面圆的半径为3.5cm，‎ 则圆锥底面周长是7π，‎ 圆锥的底面周长等于侧面展开图的扇形弧长，‎ 即扇形弧长是7π，‎ 根据弧长公式l=nπr‎180‎，‎ 得到7π=nπ•6‎‎180‎，‎ 解得：n=210°．‎ 圆锥侧面展开图的扇形圆心角为210度．‎ 点评：本题考查了圆锥侧面展开扇形圆心角与母线和底面圆半径的关系．解题思路：解决此类问题时要紧紧抓住两者之间的两个对应关系：（1）圆锥的母线长等于侧面展开图的扇形半径；（2）圆锥的底面周长等于侧面展开图的扇形弧长．正确对这两个关系的记忆是解题的关键．‎ ‎16、（2010•安顺）某校去年有学生1 000名，今年比去年增加4.4%，其中寄宿学生增加了6%，走读学生减少了2%，问该校去年有寄宿学生与走读学生各多少名设去年有寄宿学生x名，走读学生y名，则可列出的方程组为： ．‎ 考点：由实际问题抽象出二元一次方程组。‎ 分析：根据“某校去年有学生1 000名”，可得出方程为x+y=1000；根据“今年比去年增加4.4%，其中寄宿学生增加了6%，走读学生减少了2%”，得出的方程为（1+6%）x+（1﹣4%）y=1000×4.4%，列出方程组．‎ 解答：解：根据某校去年有学生1000名，得方程x+y=1000；‎ 根据今年比去年增加4.4%，其中寄宿学生增加了6%，走读学生减少了2%，得方程为（1+6%）x+（1﹣4%）y=1000×4.4%．‎ 那么方程组可列成：‎&x+y=1000‎‎&（1+6%）x+（1﹣4%）y=1000×4.4%‎．‎ 点评：根据实际问题中的条件列方程组时，要注意抓住题目中的一些关键性词语，找出等量关系，列出方程组．‎ ‎17、（2010•安顺）如图，在△ABC中，∠A=90°，分别以B、C为圆心的两个等圆外切，两圆的半径都为2cm，则图中阴影部分的面积为 cm2．‎ 考点：扇形面积的计算；相切两圆的性质。‎ 分析：根据两扇形的圆心角的度数和为90°，半径为2，结合扇形的面积公式进行计算．‎ 解答：解：∵∠A=90°，‎ ‎∴∠B+∠C=90°，‎ ‎∴阴影部分的面积=‎90π×4‎‎360‎=π（cm2）．‎ 点评：此题注意计算两个扇形的面积的时候，要运用提公因式法，整体把扇形所在的两个圆心角的和代入计算．‎ ‎18、（2010•安顺）如图是某工程队在“村村通”工程中，修筑的公路长度y（米）与时间x（天）之间的关系图象．根据图象提供的信息，可知该公路的长度是 米．‎ 考点：函数的图象。‎ 专题：分段函数。‎ 分析：本题可设x≥2时，函数解析式为y=kx+b，根据待定系数法即可求出函数解析式，进而即可求出答案．‎ 解答：解：设x≥2时，函数解析式为y=kx+b，‎ ‎∴2k+b=180，4k+b=288，‎ 解得k=54，b=72，‎ ‎∴y=54x+72，‎ ‎∴当x=8时，y=504．‎ 故填504．‎ 点评：本题用到的知识点是：已知两点，可确定直线的函数解析式．当已知函数的某一点的横坐标时，也可求出相应的y值．‎ 三、解答题（共9小题，满分88分）‎ ‎19、（2010•安顺）计算：‎﹣‎2‎‎2‎+（tan60°﹣1）×‎3‎+（﹣‎1‎‎2‎‎）‎‎﹣2‎+（﹣π‎）‎‎0‎﹣∣2﹣‎3‎∣‎．‎ 考点：特殊角的三角函数值；有理数的乘方；实数的性质；零指数幂；负整数指数幂。‎ 专题：计算题。‎ 分析：按照实数的运算法则依次计算，注意：（﹣‎1‎‎2‎）﹣2=4，（﹣π）0=1，|2﹣‎3‎|=2﹣‎3‎．‎ 解答：解：原式=﹣4+（‎3‎﹣1）‎3‎+4+1﹣2+‎‎3‎ ‎=﹣4+3﹣‎3‎+3+‎‎3‎ ‎=2．‎ 点评：本题需注意的知识点是：a﹣p=‎1‎ap，任何不等于0的数的0次幂是1，负数的绝对值是正数．‎ ‎20、（2010•安顺）化简‎（x﹣1﹣‎8‎x+1‎）÷‎x+3‎x+1‎，将x=3﹣‎‎2‎代入求值．‎ 考点：二次根式的化简求值；分式的化简求值。‎ 分析：先把原式括号里的式子通分然后根据约分的方法和二次根式的性质进行化简，最后代入计算．‎ 解答：解：原式=x‎2‎‎﹣1﹣8‎x+1‎•x+1‎x+3‎=x﹣3；‎ 当x=3﹣‎2‎，‎ 原式=3﹣‎2‎﹣3=‎﹣‎‎2‎．‎ 点评：本题主要考查分式的化简，二次根式的代值计算，代值时要细心．‎ ‎21、（2010•安顺）为了测量学校旗杆AB的高度，学校数学实践小组做了如下实验：在阳光的照射下，旗杆AB的影子恰好落在水平地面BC的斜坡坡面CD上，测得BC=20m，CD=18m，太阳光线AD与水平面夹角为30°且与斜坡CD垂直．根据以上数据，请你求出旗杆AB的高度．（结果保留根号）‎ 考点：解直角三角形的应用。‎ 分析：根据题意正确作出图形，分别在两个直角三角形中解题．‎ 设AD与BC的延长线交于E，在Rt△CDE中，CD=18，∠AEC=30°，所以CE=36，BE=56，AB=‎56‎‎3‎‎3‎．‎ 解答：解：‎ 作AD与BC的延长线，交于E点．‎ 在直角△CDE中，∠E=30°，‎ ‎∴CE=2CD=2×18=36．‎ 则BE=BC+CE=20+36=56．‎ 在直角△ABE中，tan∠E=ABBE，‎ ‎∴AB=BE•tan30°=‎56‎‎3‎‎3‎．‎ 即旗杆AB的高度是‎56‎‎3‎‎3‎m．‎ 点评：此题考查了三角函数的基本概念，主要是正切概念及运算，关键把实际问题转化为数学问题加以计算．‎ ‎22、（2010•安顺）如图，一次函数y=kx+b的图象与反比例函数y=‎mx的图象交于A（﹣3，1），B（2，n）两点，直线AB分交x轴、y轴于D，C两点．‎ ‎（1）求上述反比例函数和一次函数的解析式；‎ ‎（2）求ADCD的值．‎ 考点：反比例函数综合题。‎ 专题：计算题；待定系数法。‎ 分析：（1）反比例函数y=‎mx的图象经过点A（﹣3，1），代入解析式就得到反比例函数的解析式，再把B（2，n）代入反比例函数解析式就可以求出A的坐标，因而利用待定系数法就可以求出一次函数的解析式；‎ ‎（2）过点A作AE⊥x轴于点E．易证Rt△OCD∽Rt△EAD，则ADCD‎=‎AECO，易证．‎ 解答：解：（1）把x=﹣3，y=1代入y=‎mx，得：m=﹣3．‎ ‎∴反比例函数的解析式为y=﹣‎‎3‎x．‎ 把x=2，y=n代入y=﹣‎‎3‎x得n=﹣‎‎3‎‎2‎．‎ 把x=﹣3，y=1；x=2，y=﹣‎‎3‎‎2‎分别代入y=kx+b得‎&﹣3k+b=1‎‎&2k+b=﹣‎‎3‎‎2‎，‎ 解得‎&k=﹣‎‎1‎‎2‎‎&b=﹣‎‎1‎‎2‎，‎ ‎∴一次函数的解析式为y=﹣‎1‎‎2‎x﹣‎‎1‎‎2‎ ‎（2）过点A作AE⊥x轴于点E．‎ ‎∵A点的纵坐标为1，‎ ‎∴AE=1．‎ 由一次函数的解析式为y=﹣‎1‎‎2‎x﹣‎‎1‎‎2‎得C点的坐标为‎（0，﹣‎1‎‎2‎）‎，‎ ‎∴OC=‎‎1‎‎2‎．‎ 在Rt△OCD和Rt△EAD中，∠COD=∠AED=Rt∠，∠CDO=∠ADE，‎ ‎∴Rt△OCD∽Rt△EAD．‎ ‎∴ADCD‎=‎AECO=2．‎ 点评：本题主要考查了待定系数法求函数解析式，根据相似三角形的对应边的比相等，把求ADCD的值的问题转化为AE与CO的比值．‎ ‎23、（2010•安顺）某公司现有甲、乙两种品牌的打印机，其中甲品牌有A，B两种型号，乙品牌有C，D，E三种型号．朝阳中学计划从甲、乙两种品牌中各选购一种型号的打印机．‎ ‎（1）利用树状图或列表法写出所有选购方案；‎ ‎（2）若各种型号的打印机被选购的可能性相同，那么C型号打印机被选购的概率是多少？‎ ‎（3）各种型号打印机的价格如下表：‎ 朝阳中学购买了两种品牌的打印机共30台，其中乙品牌只选购了E型号，共用去资金5‎ 万元，问E型号的打印机购买了多少台？‎ 考点：列表法与树状图法；一元一次方程的应用。‎ 专题：方案型；图表型。‎ 分析：依据题意先用列表法或画树状图法分析所有等可能的出现结果，然后根据概率公式求出该事件的概率；‎ 根据资金得到相应的方程，求解即可．‎ 解答：解：（1）所列树状图或列表表示为：‎ 结果为：（A，C），（A，D），（A，E），（B，C），（B，D），（B，E）；‎ ‎（2）由（1）知C型号的打印机被选购的概率为‎2‎‎6‎‎=‎‎1‎‎3‎；‎ ‎（3）设选购E型号的打印机x台（x为正整数），则选购甲品牌（A或B型号）（30﹣x）台，由题意得：‎ 当甲品牌选A型号时：1000x+（30﹣x）×2000=50000，解得x=10，‎ 当甲品牌选B型号时：1000x+（30﹣x）×1700=50000，解得x=‎‎10‎‎7‎（不合题意），‎ 故E型号的打印机应选购10台．‎ 点评：本题着重考查了用树状图列举随机事件出现的所有情况，并求出某些事件的概率，但应注意在求概率时各种情况出现的可能性务必相同．用到的知识点为：概率=所求情况数与总情况数之比．‎ ‎24、（2010•安顺）已知：如图，在△ABC中，AB=AC，AD⊥BC，垂足为点D，AN是△ABC外角∠CAM的平分线，CE⊥AN，垂足为点E，‎ ‎（1）求证：四边形ADCE为矩形；‎ ‎（2）当△ABC满足什么条件时，四边形ADCE是一个正方形？并给出证明．‎ 考点：矩形的判定；角平分线的性质；等腰三角形的性质；正方形的判定。‎ 专题：证明题；开放型。‎ 分析：（1）根据矩形的有三个角是直角的四边形是矩形，已知CE⊥AN，AD⊥BC，所以求证∠DAE=90°，我样可以证明四边形ADCE为矩形．‎ ‎（2）根据正方形的判定，我们可以假设当AD=‎1‎‎2‎BC，由已知可得，DC=‎1‎‎2‎BC，由（1）的结论可知四边形ADCE为矩形，所以证得，四边形ADCE为正方形．‎ 解答：解：（1）在△ABC中，AB=AC，AD⊥BC，‎ ‎∴∠BAD=∠DAC，‎ ‎∵AN是△ABC外角∠CAM的平分线，‎ ‎∴∠MAE=∠CAE，‎ ‎∴∠DAE=∠DAC+∠CAE=‎1‎‎2‎‎×‎180°=90°，‎ 又∵AD⊥BC，CE⊥AN，‎ ‎∴∠ADC=∠CEA=90°，‎ ‎∴四边形ADCE为矩形．‎ ‎（2）给出正确条件即可．‎ 例如，当AD=‎1‎‎2‎BC时，四边形ADCE是正方形．‎ ‎∵AB=AC，AD⊥BC于D，‎ ‎∴DC=‎1‎‎2‎BC，‎ 又∵AD=‎1‎‎2‎BC，‎ ‎∴DC=AD，‎ 由（1）四边形ADCE为矩形，‎ ‎∴矩形ADCE是正方形．‎ 点评：本题是以开放型试题，主要考查了对矩形的判定，正方形的判定，等腰三角形的性质，及角平分线的性质等知识点的综合运用．‎ ‎25、（2010•安顺）为了节约用水，某水厂规定：某单元居民如果一个月的用水量不超过x吨，那么这个月该单元居民只交10元水费．如果超过x吨，则这个月除了仍要交10元水费外，超过那部分按每吨x‎100‎元交费．‎ ‎（1）该单元居民8月份用水80吨，超过了规定的x吨，则超过部分应交水费 元（用含x的式子表示）．‎ ‎（2）下表是该单元居民9月、10月的用水情况和交费情况：‎ 根据上表的数据，求该水厂规定的x吨是多少？‎ 考点：一元二次方程的应用。‎ 专题：其他问题。‎ 分析：（1）超过的用水量为（80﹣x）吨，所以，超过部分应交水费x‎100‎（80﹣x）元．‎ ‎（2）根据表格提供的数据，可以知道x≥50，根据9月份用水情况可以列出方程：10+x‎100‎（85﹣x）=25．‎ 解答：解：（1）x‎100‎（80﹣x）；‎ ‎（2）根据表格提供的数据，可以知道x≥50，根据9月份用水情况可以列出方程：‎ ‎10+x‎100‎（85﹣x）=25‎ 解得，x1=60，x2=25，‎ 因为x≥50，‎ 所以x=60．‎ 该水厂规定的x吨是60吨．‎ 点评：找到关键描述语，找到等量关系准确的列出方程是解决问题的关键．判断所求的解是否符合题意，舍去不合题意的解．‎ ‎26、（2010•安顺）如图，⊙O是△ABC的外接圆，且AB=AC，点D在弧BC上运动，过点D作DE∥BC，DE交AB的延长线于点E，连接AD、BD．‎ ‎（1）求证：∠ADB=∠E；‎ ‎（2）当点D运动到什么位置时，DE是⊙O的切线？请说明理由．‎ ‎（3）当AB=5，BC=6时，求⊙O的半径．‎ 考点：切线的判定；平行线的性质；等腰三角形的性质；勾股定理；垂径定理；圆周角定理。‎ 专题：综合题。‎ 分析：（1）根据圆周角定理及平行线的性质不难求解；‎ ‎（2）要使DE是圆的切线，那么D就是求点，AD⊥DE，又根据AD过圆心O，BC∥ED，根据垂径定理可得出D应是弧BC的中点．‎ ‎（3）可通过构建直角三角形来求解，连接BO、AO，并延长AO交BC于点F，根据垂径定理BF=CF，AF=R+OF，那么直角三角形OBF中可以用R表示出OF，OB，然后根据勾股定理求出半径的长．‎ 解答：解：（1）在△ABC中，‎ ‎∵AB=AC，‎ ‎∴∠ABC=∠C．‎ ‎∵DE∥BC，‎ ‎∴∠ABC=∠E，‎ ‎∴∠E=∠C，‎ 又∵∠ADB=∠C，‎ ‎∴∠ADB=∠E；‎ ‎（2）当点D是弧BC的中点时，DE是⊙O的切线．‎ 理由是：当点D是弧BC的中点时，则有AD⊥BC，且AD过圆心O，‎ 又∵DE∥BC，‎ ‎∴AD⊥ED．‎ ‎∴DE是⊙O的切线；‎ ‎（3）连接BO、AO，并延长AO交BC于点F，‎ 则AF⊥BC，且BF=BC=3，‎ 又∵AB=5，‎ ‎∴AF=4；‎ 设⊙O的半径为r，在Rt△OBF中，OF=4﹣r，OB=r，BF=3，‎ ‎∴r2=32+（4﹣r）2‎ 解得r=‎25‎‎8‎，‎ ‎∴⊙O的半径是‎25‎‎8‎．‎ 点评：本题主要考查了圆周角定理，切线的判定，平行线的性质，垂径定理等知识点，正确运用好圆心角，弧，弦的关系是解题的关键．‎ ‎27、（2010•安顺）如图，抛物线y=‎﹣‎‎3‎‎4‎x2+3与x轴交于点A，点B，与直线y=‎﹣‎‎3‎‎4‎x+b相交于点B，点C，直线y=‎﹣‎‎3‎‎4‎x+b与y轴交于点E．‎ ‎（1）写出直线BC的解析式．‎ ‎（2）求△ABC的面积．‎ ‎（3）若点M在线段AB上以每秒1个单位长度的速度从A向B运动（不与A，B重合），同时，点N在射线BC上以每秒2个单位长度的速度从B向C运动．设运动时间为t秒，请写出△MNB的面积S与t的函数关系式，并求出点M运动多少时间时，△MNB的面积最大，最大面积是多少？‎ 考点：二次函数综合题。‎ 专题：压轴题。‎ 分析：（1）令y=0代入y=‎﹣‎‎3‎‎4‎x2+3求出点A，B的坐标．把B点坐标代入y=‎﹣‎‎3‎‎4‎x+b求出BC的解析式．‎ ‎（2）联立方程组求出B．C的坐标．求出AB，CD的长后可求出三角形ABC的面积．‎ ‎（3）过N点作NP⊥MB，证明△BNP∽△BEO，由已知令y=0求出点E的坐标，利用线段比求出NP，BE的长．求出S与t的函数关系式后利用二次函数的性质求出S的最大值．‎ 解答：解：（1）在y=‎﹣‎‎3‎‎4‎x2+3中，令y=0‎ ‎∴‎﹣‎‎3‎‎4‎x2+3=0‎ ‎∴x1=2，x2=﹣2‎ ‎∴A（﹣2，0），B（2，0）（2分）‎ 又点B在y=‎﹣‎‎3‎‎4‎x+b上 ‎∴‎0=﹣‎3‎‎2‎+b，‎b=‎‎3‎‎2‎ ‎∴BC的解析式为y=‎﹣‎‎3‎‎4‎x+‎3‎‎2‎．（2分）‎ ‎（2）由‎&y=﹣‎3‎‎4‎x‎2‎+3‎‎&y=﹣‎3‎‎4‎x+‎‎3‎‎2‎，‎ 得‎&x‎1‎=﹣1‎‎&y‎1‎=‎‎9‎‎4‎，‎&x‎2‎=2‎‎&y‎2‎=0‎．‎ ‎∴C（﹣1，‎9‎‎4‎）‎，B（2，0），（2分）‎ ‎∴AB=4，CD=‎‎9‎‎4‎，‎ ‎∴S‎△ABC‎=‎1‎‎2‎×4×‎9‎‎4‎=‎‎9‎‎2‎．（2分）‎ ‎（3）过点N作NP⊥MB于点P ‎∵EO⊥MB ‎∴NP∥EO ‎∴△BNP∽△BEO ‎∴BNBE‎=‎NPEO（1分）‎ 由直线y=﹣‎3‎‎4‎x+‎‎3‎‎2‎可得：‎E（0，‎3‎‎2‎）‎ ‎∴在△BEO中，BO=2，EO=‎3‎‎2‎，则BE=‎‎5‎‎2‎ ‎∴‎2t‎5‎‎2‎‎=‎NP‎3‎‎2‎，‎ ‎∴NP=‎6‎‎5‎t（1分）‎ ‎∴S=‎1‎‎2‎.‎6‎‎5‎t．（4﹣t）=﹣‎3‎‎5‎t2+‎12‎‎5‎t（0＜t＜4）=﹣‎3‎‎5‎（t﹣2）2+‎12‎‎5‎（1分）‎ ‎∵此抛物线开口向下，‎ ‎∴当t=2时，S最大=‎‎12‎‎5‎ ‎∴当点M运动2秒时，△MNB的面积达到最大，最大为‎12‎‎5‎．（1分）‎ 点评：本题考查的是二次函数图象与应用相结合的综合题，以及三角形面积的计算方法，难度较大．‎ 参与本试卷答题和审题的老师有：‎ zhangchao；CJX；yangjigang；haoyujun；zhjh；lihongfang；cook2360；jinlaoshi；ln_86；lbz；MMCH；wdxwwzy；csiya；zhehe；lanchong；mmll852；zhqd；leidan；lzhzkkxx；lanyuemeng；hnaylzhyk；算术；HJJ；张伟东；zxw；Linaliu；fuaisu；nhx600；feng；kuaile；xinruozai；137-hui；huangling；路斐斐。（排名不分先后）‎ ‎2011年2月17日