高中数学必修2教案：3_3_3点到直线的距离 (2)

高中数学必修2教案：3_3_3点到直线的距离 (2)

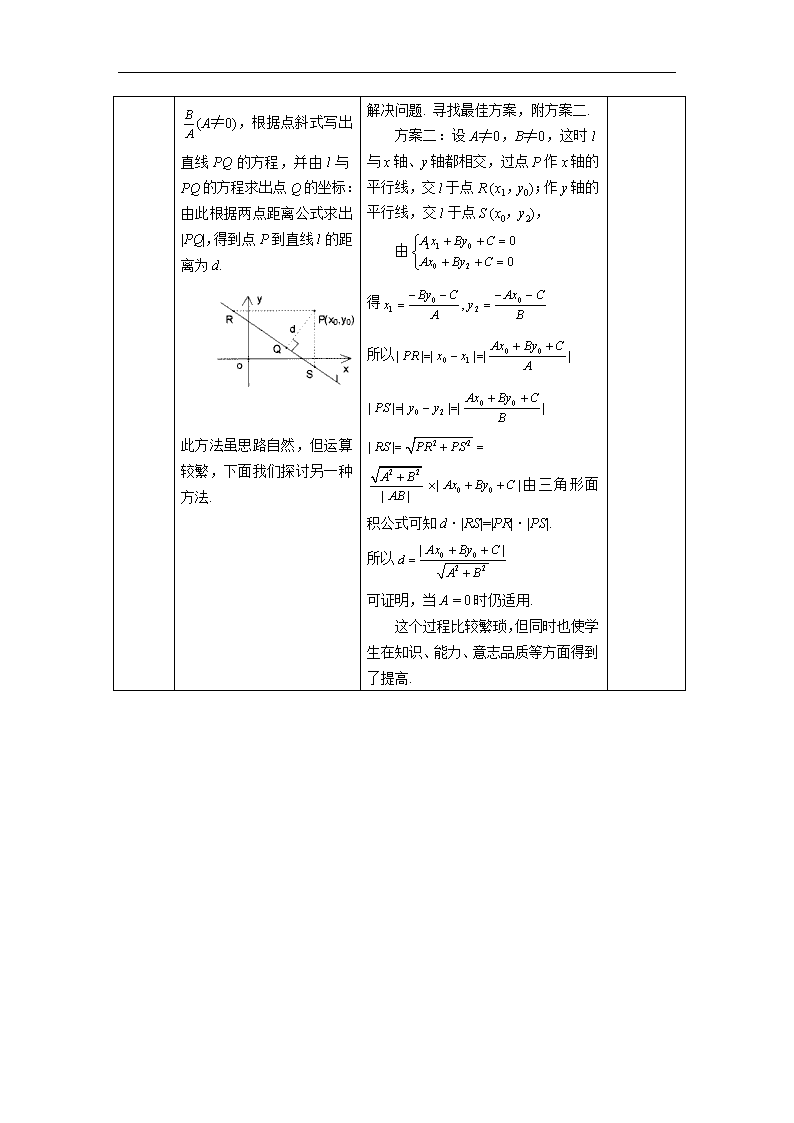
‎3.3.3 点到直线的距离 ‎（一）教学目标 ‎1．知识与技能 理解点到直线距离公式的推导，熟练掌握点到直线距离公式.‎ ‎2．过程和方法 会用点到直线距离公式求解两平行线距离.‎ ‎3．情感和价值 认识事物之间在一定条件下的转化，用联系的观点看问题.‎ ‎（二）教学重点、难点 教学重点：点到直线的距离公式.‎ 教学难点：点到直线距离公式的理解与应用.‎ ‎（三）教学方法 学导式 教学环节 教学内容 师生互动 设计意图 复习引入 前面几节课，我们一起研究学习了两直线的平行或垂直的充要条件，两直线的夹角公式，两直线的交点问题，两点间的距离公式。逐步熟悉了利用代数方法研究几何问题的思想方法.这一节，我们将研究怎样由点的坐标和直线的方程求点P到直线l的距离.‎ 用POWERPOINT打出平面直角坐标系中两直线，进行移动，使学生回顾两直线的位置关系，且在直线上取两点，让学生指出两点间的距离公式，复习前面所学.要求学生思考点到直线的距离的计算？能否用两点间距离公式进行推导？‎ 设置情境导入新课 概念形成 ‎1．点到直线距离公式 点P (x0，y0)到直线l：Ax + By + C = 0的距离为 推导过程 方案一：‎ 设点P到直线l的垂线段为PQ，垂足为Q，由PQ⊥‎ ‎（1）教师提出问题 已知P (x0，y0)，直线l：Ax + By + C = 0，怎样用点的坐标和直线方程直接求点P到直线l的距离呢？‎ 学生自由讨论 ‎（2）数形结合，分析问题，提出解决方案.‎ 把点到直线l的距离转化为点P到l的垂线段的长，即点到点的距离.‎ 通过这种转化，培养学生“化归”的思想方法.‎ l可知，直线PQ的斜率为(A≠0)，根据点斜式写出直线PQ的方程，并由l与PQ的方程求出点Q的坐标：由此根据两点距离公式求出|PQ|，得到点P到直线l的距离为d.‎ 此方法虽思路自然，但运算较繁，下面我们探讨另一种方法.‎ 画出图形，分析任务，理清思路，解决问题. 寻找最佳方案，附方案二.‎ 方案二：设A≠0，B≠0，这时l与x轴、y轴都相交，过点P作x轴的平行线，交l于点R (x1，y0)；作y轴的平行线，交l于点S (x0，y2)，‎ 由 得 所以 由三角形面积公式可知d·|RS|=|PR|·|PS|.‎ 所以 可证明，当A = 0时仍适用.‎ 这个过程比较繁琐，但同时也使学生在知识、能力、意志品质等方面得到了提高.‎ 应用举例 例1 求点P = (–1，2 )到直线3x = 2的距离.‎ ‎ 解：‎ 例2 已知点A (1，3)，B (3，1)，C(–1，0)，求三角形ABC的面积. ‎ 学生分析求解，老师板书 例2 解：设AB边上的高为h，则 AB边上的高h就是点C到AB的距离.‎ AB边所在直线方程为 即x + y – 4 = 0.‎ 点C到x + y – 4 = 0的距离为h ‎，‎ 因此，‎ 通过这两道简单的例题，使学生能够进一步对点到直线的距离理解应用，能逐步体会用代数运算解决几何问题的优越性.‎ 概念深化 ‎2．两平行线间的距离d 已知l1：Ax + By + C1 = 0‎ l2：Ax + By + C2 = 0‎ 证明：设P0 (x0，y0)是直线Ax + By + C2 = 0上任一点，则点P0到直线Ax + By + C1 = 0的距离为 ‎.‎ 又Ax0 + By0 + C2 = 0‎ 即Ax0 + By0= –C2，‎ 教师提问：‎ 能不能把两平行直线间距离转化为点到直线的距离呢？‎ 学生交流后回答.‎ 再写出推理过程 进一步培养学生化归转化的思想.‎ ‎∴‎ 应用举例 例3 求两平行线 l1：2x + 3y – 8 = 0‎ l2：2x + 3y – 10 =0的距离.‎ 解法一：在直线l1上取一点P(4,0)，因为l1∥l2，所以P到l2的距离等于l1与l2的距离，于是 解法二：直接由公式 课堂练习：已知一直线被两平行线3x + 4y – 7 = 0与3x + 4y + 8 = 0所截线段长为3，且该直线过点(2，3)，求该直线方程.‎ ‎ 在教师的引导下，学生分析思路，再由学生上台板书.‎ 开拓学生思维，培养学生解题能力.‎ 归纳总结 老师和学生共同总结——交流——完善 ‎ 小结：点到直线距离公式的推导过程，点到直线的距离公式，能把求两平行线的距离转化为点到直线的距离公式.‎ 培养学生归纳、概括能力，构建知识网络.‎ 课后作业 布置作业 见习案3.3的第三课时 独立完成 巩固深化 备选例题 例1 求过点M(–2，1)且与A(–1，2)，B(3，0)两点距离相等的直线的方程.‎ 解法一：当直线斜率不存在时，直线为x = –2，它到A、B两点距离不相等.‎ 所以可设直线方程为：y – 1 = k(x + 2)即kx – y + 2k + 1 = 0.‎ 由，‎ 解得k = 0或.‎ 故所求的直线方程为y – 1 = 0或x + 2y = 0.‎ 解法二：由平面几何知识：l∥AB或l过AB的中点.‎ 若l∥AB且，则l的方程为x + 2y = 0.‎ 若l过AB的中点N(1，1)则直线的方程为y = 1.‎ 所以所求直线方程为y – 1 = 0或x + 2y = 0.‎ 例2 （1）求直线2x + 11y + 16 = 0关于点P(0，1)对称的直线方程.‎ ‎（2）两平行直线3x + 4y – 1 = 0与6x + 8y + 3 = 0关于直线l对称，求l的方程.‎ ‎【解析】（1）当所求直线与直线2x + 11y + 16 = 0平行时，可设直线方程为2x + 11y + C=0‎ 由P点到两直线的距离相等，即 ‎，所以C = –38.‎ 所求直线的方程为2x + 11y – 38 = 0.‎ ‎（2）依题可知直线l的方程为：6x + 8y + C = 0.‎ 则它到直线6x + 8y – 2 = 0的距离，‎ 到直线6x + 8y + 3 = 0的距离为 所以d1 = d2即，所以.‎ 即l的方程为：.‎ 例3 等腰直角三角形ABC的直角顶点C和顶点B都在直线2x + 3y – 6 = 0上，顶点A 的坐标是(1，–2).求边AB、AC所在直线方程.‎ ‎【解析】已知BC的斜率为，因为BC⊥AC 所以直线AC的斜率为，从而方程 即3x – 2y – 7 = 0‎ 又点A(1，–2)到直线BC：2x + 3y – 6 = 0的距离为，‎ 且.‎ 由于点B在直线2x + 3y – 6 = 0上，可设，‎ 且点B到直线AC的距离为 所以或，所以或 所以或 所以直线AB的方程为或 即x – 5y – 11 = 0或5x + y – 3 = 0‎ 所以AC的直线方程为：3x – 2y – 7 = 0‎ AB的直线方程为：x – 5y – 11 = 0或5x + y – 3 = 0.‎