高中数学必修2教案：2_3_1直线与平面垂直的判定 (2)

高中数学必修2教案：2_3_1直线与平面垂直的判定 (2)

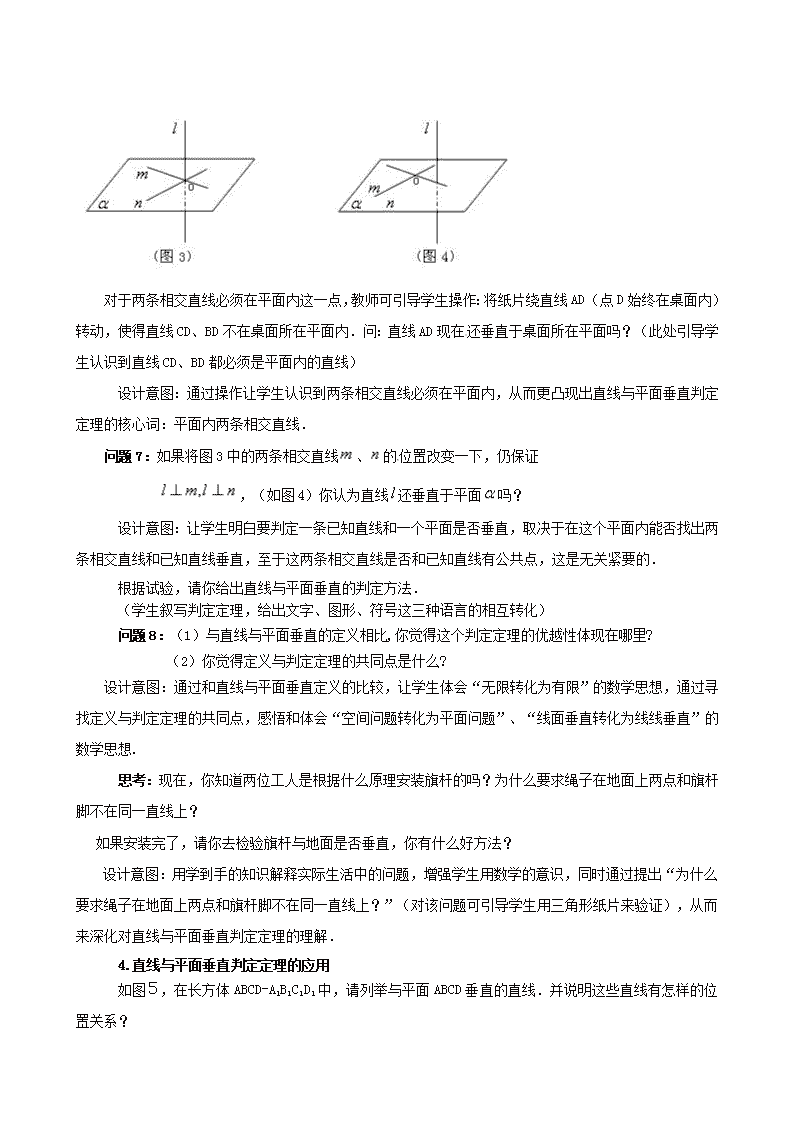
‎2. 3.1‎直线与平面垂直的判定 ‎【教学目标】‎ ‎ 1.借助对实例、图片的观察，提炼直线与平面垂直的定义，并能正确理解直线与平面垂直的定义；‎ ‎ 2.通过直观感知，操作确认，归纳直线与平面垂直的判定定理，并能运用判定定理证明一些空间位置关系的简单命题；‎ ‎3.在探索直线与平面垂直判定定理的过程中发展合情推理能力，同时感悟和体验“空间问题转化为平面问题”、“线面垂直转化为线线垂直”、“无限转化为有限”等数学思想.‎ ‎【教学重难点】‎ 教学重点：运用判定定理证明一些空间位置关系的简单命题。‎ 教学难点：运用判定定理证明一些空间位置关系的简单命题。‎ ‎【教学过程】‎ ‎1. 从实际背景中感知直线与平面垂直的形象 ‎ 问题1：空间一条直线和一个平面有哪几种位置关系？‎ ‎ 问题2：在日常生活中你见得最多的直线与平面相交的情形是什么？请举例说明． ‎ ‎ 设计意图：此问基于学生的客观现实，通过对生活事例的观察，让学生直观感知直线与平面相交中一种特例：直线与平面垂直的初步形象，激起进一步探究直线与平面垂直的意义．‎ ‎2.提炼直线与平面垂直的定义 ‎ 问题3：你能给出直线和平面垂直的定义吗？回忆一下直线与直线垂直是如何定义的？ ‎ ‎ 设计意图：两直线垂直有相交垂直和异面垂直，而异面直线垂直是转化为两直线相交垂直，实质上是将空间问题转化为平面问题，让学生回忆直线与直线垂直的定义，旨在由此得到启发：用“平面化”的思想来思考问题，即能否用一条直线垂直于一个平面内的直线，来定义这条直线与这个平面垂直？ ‎ ‎ 问题4：结合对下列问题的思考，试着给出直线和平面垂直的定义． ‎ ‎ (1)阳光下，旗杆AB与它在地面上的影子BC所成的角度是多少？‎ ‎ (2)随着太阳的移动,影子BC的位置也会移动,而旗杆AB与影子BC所成的角度是否会发生改变?‎ ‎ (3)旗杆AB与地面上任意一条不过点B的直线B‎1C1的位置关系如何?依据是什么 设计意图：主要引导学生通过观察直立于地面的旗杆与它在地面的影子的位置关系来分析、归纳直线与平面垂直这一概念．‎ ‎ （学生叙写定义，并建立文字、图形、符号这三种语言的相互转化）‎ ‎ 思考：（1）如果一条直线垂直于一个平面内的无数条直线，那么这条直线是否与这个平面垂直？‎ ‎ （2）如果一条直线垂直于一个平面，那么这条直线是否垂直于这个平面内的所有直线？（对问（1），在学生回答的基础上用直角三角板在黑板上直观演示；对问（2）可引导学生给出符号语言表述：若，则)‎ ‎ 设计意图：通过对问题（1）的辨析讨论，深化直线与平面垂直的概念．通过对问题（2）的辨析讨论旨在让学生掌握线线垂直的一种判定方法．‎ ‎ 通常定义可以作为判定依据，但由于利用直线与平面垂直的定义直接判定直线与平面垂直需要考察平面内的每一条直线与已知直线是否垂直，这给我们的判定带来困难，因为我们无法去一一检验．这就有必要去寻找比定义法更简捷、可行的直线与平面垂直的判定方法．‎ ‎ 3.探究直线与平面垂直的判定定理 ‎ 创设情境  猜想定理：某公司要安装一根‎8米高的旗杆，两位工人先从旗杆的顶点挂两条长‎10米的绳子，然后拉紧绳子并把绳子的下端放在地面上两点（和旗杆脚不在同一直线上）．如果这两点都和旗杆脚距离‎6米，那么表明旗杆就和地面垂直了，你知道这是为什么吗？ ‎ 设计意图：引导学生根据直观感知以及已有经验，进行合情推理，猜想判定定理．‎ ‎ 学生活动：（折纸试验）请同学们拿出一块三角形纸片，我们一起做一个试验：过三角形的顶点A翻折纸片，得到折痕AD（如图1），将翻折后的纸片竖起放置在桌面上（BD、DC与桌面接触）‎ ‎                 ‎ 问题5：（1）折痕AD与桌面垂直吗？‎ ‎  （2）如何翻折才能使折痕AD与桌面所在的平面垂直？（组织学生动手操作、探究、确认）‎ ‎ 设计意图：通过折纸让学生发现当且仅当折痕AD是BC边上的高时，且B、D、C不在同一直线上的翻折之后竖起的折痕AD才不偏不倚地站立着，即AD与桌面垂直（如图2），其它位置都不能使AD与桌面垂直． ‎ ‎ 问题6：在你翻折纸片的过程中，纸片的形状发生了变化，这是变的一面，那么不变的一面是什么呢？（可从线与线的关系考虑）如果我们把折痕抽象为直线，把BD、CD抽象为直线，把桌面抽象为平面(如图3)，那么你认为保证直线与平面垂直的条件是什么？‎ 对于两条相交直线必须在平面内这一点，教师可引导学生操作：将纸片绕直线AD（点D始终在桌面内）转动，使得直线CD、BD不在桌面所在平面内．问：直线AD现在还垂直于桌面所在平面吗？（此处引导学生认识到直线CD、BD都必须是平面内的直线）‎ ‎ 设计意图：通过操作让学生认识到两条相交直线必须在平面内，从而更凸现出直线与平面垂直判定定理的核心词：平面内两条相交直线．‎ 问题7：如果将图3中的两条相交直线、的位置改变一下，仍保证 ‎ ，（如图4）你认为直线还垂直于平面吗？‎ ‎ 设计意图：让学生明白要判定一条已知直线和一个平面是否垂直，取决于在这个平面内能否找出两条相交直线和已知直线垂直，至于这两条相交直线是否和已知直线有公共点，这是无关紧要的．‎ ‎ 根据试验，请你给出直线与平面垂直的判定方法．‎ ‎ （学生叙写判定定理，给出文字、图形、符号这三种语言的相互转化）‎ ‎ 问题8：（1）与直线与平面垂直的定义相比,你觉得这个判定定理的优越性体现在哪里?‎ ‎（2）你觉得定义与判定定理的共同点是什么? ‎ 设计意图：通过和直线与平面垂直定义的比较，让学生体会“无限转化为有限”的数学思想，通过寻找定义与判定定理的共同点，感悟和体会“空间问题转化为平面问题”、“线面垂直转化为线线垂直”的数学思想.‎ ‎ 思考：现在，你知道两位工人是根据什么原理安装旗杆的吗？为什么要求绳子在地面上两点和旗杆脚不在同一直线上？ ‎ 如果安装完了，请你去检验旗杆与地面是否垂直，你有什么好方法？‎ ‎ 设计意图：用学到手的知识解释实际生活中的问题，增强学生用数学的意识，同时通过提出 “为什么要求绳子在地面上两点和旗杆脚不在同一直线上？”（对该问题可引导学生用三角形纸片来验证），从而来深化对直线与平面垂直判定定理的理解．‎ ‎ 4.直线与平面垂直判定定理的应用 ‎ 如图５，在长方体ABCD-A1B‎1C1D1中，请列举与平面ABCD垂直的直线．并说明这些直线有怎样的位置关系？‎ ‎  ‎ 思考：如图６，已知，则吗？请说明理由． （分别用直线与平面垂直的判定定理、直线与平面垂直的定义证明；并让学生用语言叙述：如果两条平行直线中的一条直线垂直于一个平面，那么另一条直线也垂直于这个平面）‎ ‎ 设计意图：这个例题给出了判断直线和平面垂直的一个常用的命题，这个命题体现了平行关系与垂直关系之间的联系．‎ 练习：如图７，在三棱锥V-ABC中 ，VA＝VC,AB＝BC,K是AC的中点．‎ ‎ ‎ 求证：AC⊥平面VKB 思考：‎ ‎ (1)在三棱锥V-ABC中，VA＝VC，AB＝BC，求证：VB⊥AC；‎ ‎ (2)在⑴中，若E、F分别是AB、BC 的中点，试判断EF与平面VKB的位置关系； ‎ ‎  (3)在⑵的条件下，有人说“VB⊥AC， VB⊥EF， ∴VB⊥平面ABC”，对吗？‎ ‎ 设计意图：例2重在对直线与平面垂直判定定理的应用．变式（1）在例2的基础上，应用了直线与平面垂直的意义；变式（2）是对例1判定方法的应用；变式（3）的判断在于进一步巩固直线与平面垂直的判定定理．3个小题环环相扣，汇集了本节课的学习内容，突出了知识间内在联系和融会贯通． ‎ ‎5.总结反思，当堂检测 ‎（1）本节课你学会了哪些判断直线与平面垂直的方法？试用自己理解的语言叙述．‎ ‎（2）直线与平面垂直的判定定理中体现了哪些数学思想方法？‎ ‎  检测设计 ‎ 1．课本探究：如图2.3-7，直四棱柱A1B‎1C1D1-ABCD（侧棱与底面垂直的棱柱称为直棱柱）中，底面四边形ABCD满足什么条件时，A‎1C⊥B1D1．‎ ‎ 2．如图９，PA⊥平面ABC，BC⊥AC，写出图中所有的直角三角形．‎ ‎ 　　　　　 ‎ ‎【板书设计】‎ 一、直线与平面垂直的定义 二、直线与平面垂直的判定定理 三、例题 例1‎ 变式1‎ ‎ 【作业布置】课本练习2‎ ‎ ‎ ‎2.3.1‎直线与平面垂直的判定导学案 课前预习学案 一、预习目标：‎ 借助对实例、图片的观察，提炼直线与平面垂直的定义，并能正确理解直线与平面垂直的定义；‎ 二、预习内容：问题1：空间一条直线和一个平面有哪几种位置关系？‎ 问题2：在日常生活中你见得最多的直线与平面相交的情形是什么？请举例说明．‎ ‎ 问题3：你能给出直线和平面垂直的定义吗？回忆一下直线与直线垂直是如何定义的？ ‎ 问题4：结合对下列问题的思考，试着给出直线和平面垂直的定义．‎ ‎(1)阳光下，旗杆AB与它在地面上的影子BC所成的角度是多少？‎ ‎ (2)随着太阳的移动,影子BC的位置也会移动,而旗杆AB与影子BC所成的角度是否会发生改变?‎ ‎(3)旗杆AB与地面上任意一条不过点B的直线B‎1C1的位置关系如何?依据是什么 直线与直线垂直是的定义________________________________________________________________‎ ‎ 思考：（1）如果一条直线垂直于一个平面内的无数条直线，那么这条直线是否与这个平面垂直？‎ ‎（2）如果一条直线垂直于一个平面，那么这条直线是否垂直于这个平面内的所有直线？‎ ‎(3) 如何判定一条直线直线和平面垂直呢？‎ 三． 提出疑惑 同学们，通过你的自主学习，你还有那些疑惑，请填在下面的表格中 疑惑点 疑惑内容 课内探究学案 一、学习目标： ‎ ‎（1）探究出直线与平面垂直的判定定理 ‎（2）利用定理解决实际问题 学习重点：运用判定定理证明一些空间位置关系的简单命题。‎ 学习难点：运用判定定理证明一些空间位置关系的简单命题。‎ 二、学习过程 ‎1、探究判定定理 学生活动：（折纸试验）请同学们拿出一块三角形纸片，我们一起做一个试验：过三角形的顶点A翻折纸片，得到折痕AD（如图1），将翻折后的纸片竖起放置在桌面上（BD、DC与桌面接触）‎ ‎                 ‎ 问题1：（1）折痕AD与桌面垂直吗？‎ ‎（2）如何翻折才能使折痕AD与桌面所在的平面垂直？‎ ‎ ‎ 问题2：在你翻折纸片的过程中，纸片的形状发生了变化，这是变的一面，那么不变的一面是什么呢？（可从线与线的关系考虑）如果我们把折痕抽象为直线，把BD、CD抽象为直线，把桌面抽象为平面(如图3)，那么你认为保证直线与平面垂直的条件是什么？‎ ‎ ‎ 思考：现在，你知道两位工人是根据什么原理安装旗杆的吗？为什么要求绳子在地面上两点和旗杆脚不在同一直线上？‎ 如果安装完了，请你去检验旗杆与地面是否垂直，你有什么好方法？‎ 问题3：如果将图3中的两条相交直线、的位置改变一下，仍保证 ，（如图4）你认为直线还垂直于平面吗？‎ 直线与平面垂直的判定定理（文字，图形和符号三种形式）‎ 问题4： （1）与直线与平面垂直的定义相比,你觉得这个判定定理的优越性体现在哪里?‎ ‎（2）你觉得定义与判定定理的共同点是什么? ‎ ‎2、直线与平面垂直判定定理的应用 ‎ 如图５，在长方体ABCD-A1B‎1C1D1中，请列举与平面ABCD垂直的直线．并说明这些直线有怎样的位置关系？‎ ‎ ‎ 思考：如图６，已知，则吗？请说明理由．‎ 练习：如图７，在三棱锥V-ABC中 ，VA＝VC,AB＝BC,K是AC的中点．‎ ‎ ‎ 求证：AC⊥平面VKB 思考：‎ ‎ (1)在三棱锥V-ABC中，VA＝VC，AB＝BC，求证：VB⊥AC；‎ ‎ (2)在⑴中，若E、F分别是AB、BC 的中点，试判断EF与平面VKB的位置关系； ‎ ‎  (3)在⑵的条件下，有人说“VB⊥AC， VB⊥EF， ∴VB⊥平面ABC”，对吗？‎ ‎3、当堂检测设计 ‎ 1．课本探究：如图2.3-7，直四棱柱A1B‎1C1D1-ABCD（侧棱与底面垂直的棱柱称为直棱柱）中，底面四边形ABCD满足什么条件时，A‎1C⊥B1D1．‎ ‎ 2．如图９，PA⊥平面ABC，BC⊥AC，写出图中所有的直角三角形．‎ ‎ 　　　　　 ‎ ‎3．课本练习2‎ 课后练习与提高 ‎1．下列关于直线与平面的命题中，真命题是 （ ）‎ 若且，则 若且，则 若且，则 且，则 ‎ ‎2．已知直线a、b和平面M、N，且，那么 （ ） ‎ ‎（A）∥Mb⊥a （B）b⊥ab∥M ‎（C）N⊥Ma∥N （D） ‎ ‎3．在正方体中，点在侧面及其边界上运动，并且保持，则动点的轨迹为 （ ）‎ 线段 线段 ‎ 的中点与的中点连成的线段 的中点与的中点连成的线段 ‎4．三条不同的直线，、、为三个不同的平面 ‎ ①若∥ ②若∥.‎ ‎ ③若、 ④若∥‎ ‎ 上面四个命题中真命题的个数是 ‎ ‎5．如图，矩形所在的平面，分别是的中点，‎ ‎（1）求证：平面； （2）求证：‎ ‎（3）若，求证：平面 参考答案1B‎2A34②④5略