- 2021-02-26 发布 |
- 37.5 KB |
- 4页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
余角和补角教案
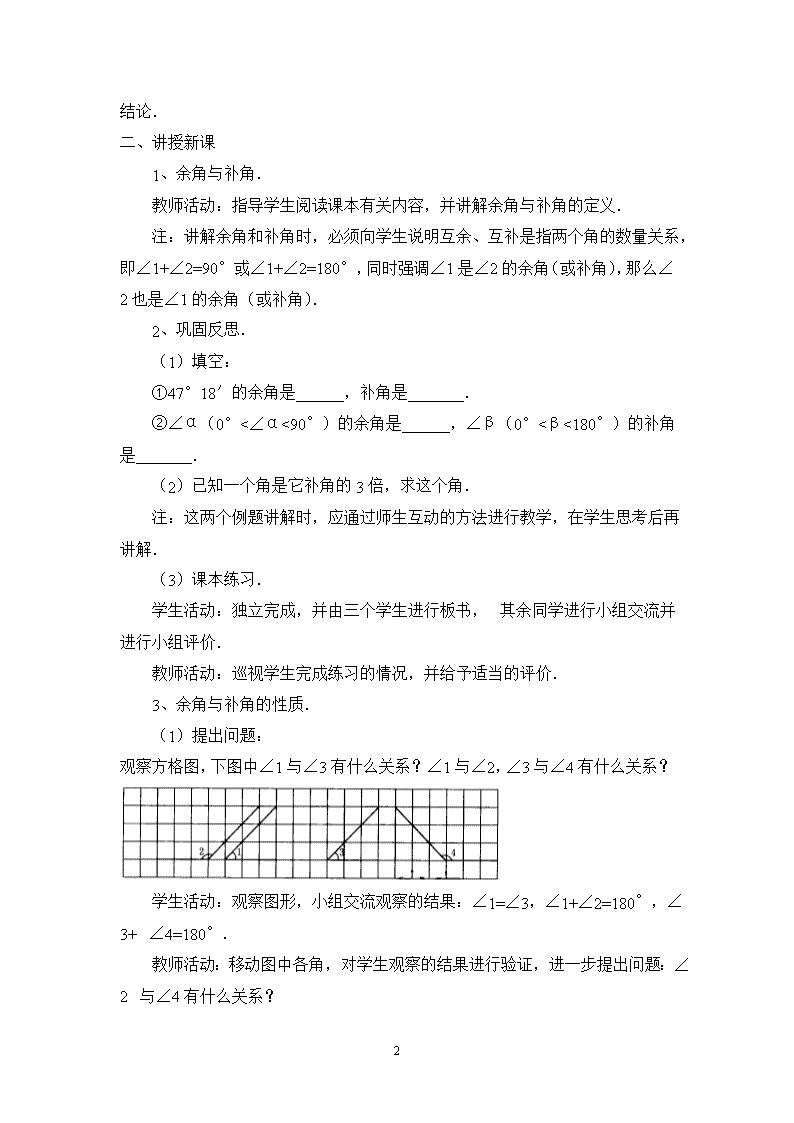
4 .3.3 余角和补角 教学目标: 1、在具体的现实情境中,认识一个角的余角与补角,掌握余角和补角的性质;了解方位角,能确定具体物体的方位。 2、进一步提高学生的抽象概括能力,发展空间观念和知识运用能力,学会简单的逻辑推理,并能对问题的结论进行合理的猜想。 3、体会观察、归纳、推理对数学知识中获取数学猜想和论证的重要作用,初步数学中推理的严谨性和结论的确定性,能在独立思考和小组交流中获益。 重点:认识角的互余、互补关系及其性质,确定方位 难点:通过简单的推理,归纳出余角、补角的性质,并能用规范的语言描述性质 教学过程 一、引入新课 1、提出问题: (1)在一副三角板中,每块都有一个角是90°,那么其余两个角的和是多少? (2)已知∠1=36°,∠2=54°,那么∠1+∠2=? 学生活动:独立思考,小组交流,得出结论:都是90°. 2.提出问题. (1)观察方格如下图中的两个角,你能猜想∠1+∠2等于多少度? (2)如果∠1=144°,∠2=36°,那么∠1+∠2=? 学生活动:观察思考,小组交流,得出结论:都是180°. 教师活动:操作多媒体,移动∠2,使∠1、∠2顶点和一边重合,引导学生观察∠1,∠ 4 2的另一条边,观察到两角的另一条边成一条直线,验证学生的结论. 二、讲授新课 1、余角与补角. 教师活动:指导学生阅读课本有关内容,并讲解余角与补角的定义. 注:讲解余角和补角时,必须向学生说明互余、互补是指两个角的数量关系,即∠1+∠2=90°或∠1+∠2=180°,同时强调∠1是∠2的余角(或补角),那么∠2也是∠1的余角(或补角). 2、巩固反思. (1)填空: ①47°18′的余角是______,补角是_______. ②∠α(0°<∠α<90°)的余角是______,∠β(0°<β<180°)的补角是_______. (2)已知一个角是它补角的3倍,求这个角. 注:这两个例题讲解时,应通过师生互动的方法进行教学,在学生思考后再讲解. (3)课本练习. 学生活动:独立完成,并由三个学生进行板书,其余同学进行小组交流并进行小组评价. 教师活动:巡视学生完成练习的情况,并给予适当的评价. 3、余角与补角的性质. (1)提出问题: 观察方格图,下图中∠1与∠3有什么关系?∠1与∠2,∠3与∠4有什么关系? 学生活动:观察图形,小组交流观察的结果:∠1=∠3,∠1+∠2=180°,∠3+∠4=180°. 教师活动:移动图中各角,对学生观察的结果进行验证,进一步提出问题:∠2与∠4有什么关系? 4 学生活动:观察思考后得出∠2=∠4. (2)说明理由: 注:教学中,向学生说明,以上从观察图形得出的结论,还应从理论上说明其理由,并讲解课本例1. 例1.如上图,∠1与∠2互补,∠3与∠4互补,如果∠1=∠3,那么∠2与∠4相等吗?为什么? 教师活动:指导学生分析题意,并写出说理过程,归纳性质. 学生活动:完成课本分析中的问题,并在教师指导下,用自己的语言描述余角、补角的性质. 板书:等角的补角相等. 师生互动:类比补角的性质,得出余角的性质. 板书:等角的余角相等. 三、巩固练习 1、如右图,∠EDC=∠CDF=90°,∠1=∠2. (1)图中哪些角互为余角?哪些角互为补角? (2)∠ADC与∠BDC有什么关系?为什么? (3)∠ADF与∠BDE有什么关系?为什么? 学生活动:独立完成练习,并进行小组交流和自我评价. 教师活动:巡视学生完成练习情况,并进行个别指导,然后进行讲评. 2、认识方位角. 提出问题:课本例2. 如下图,货轮O在航行过程中,发现灯塔A在它南偏东60°的方向上,同时,在它北偏东40°,南偏西10°,西北(即北偏西45°)方向上分别发现了客轮B、货轮C和海岛D.仿照表示灯塔方位的方法,画出客轮B、货轮C和海岛D方向的射线. 4 注:讲解时应讲清楚方位角是以正北或正南方向的射线为一个角的始边,而表示物体运动的方向的射线是角的另一边. 学生活动:在教师指导下画出问题中的每一条射线. 3、知识拓展 提出问题:、小宁从A地向东北方向走62米到B地,再从B地向西走56米到C地,这时她离A地多少米?在A地的北偏西多少度?画出图形(用1cm表示10m),然后用刻度尺和量角器进行测量.(精确到1m、1°) 学生活动:先进行小组讨论,然后独立完成,再进行小组交流和评价. 教师活动:指导学生画图和测量,并对学生完成的情况进行评价. 四、课堂小结 1、本节课学习了余角和补角,并通过简单的推理,得出余角和补角的性质. 2、了解方位角,学会确定物体运动的方向 五、作业布置 4 查看更多