中考数学试题专题等腰三角形与勾股定理试题

中考数学试题专题等腰三角形与勾股定理试题

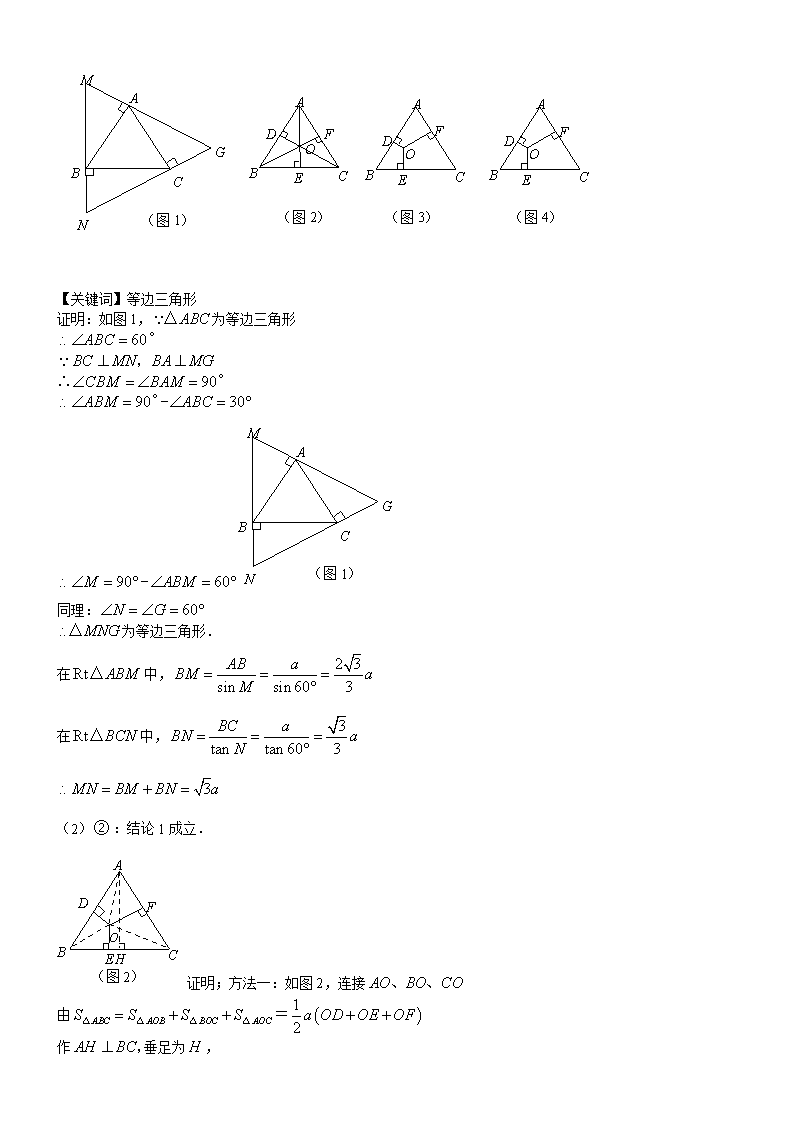
N M A G C B A F C E B D A F C E B D ‎（图1）‎ ‎（图2）‎ ‎（图3）‎ O A F C E B D ‎（图4）‎ O O ‎【关键词】等边三角形 证明：如图1，为等边三角形 ‎∴‎ N M A G C B ‎（图1）‎ 同理：‎ 为等边三角形．‎ 在中，‎ 在中，‎ ‎（2）：结论1成立．‎ A F C E B D ‎（图2）‎ O H 证明；方法一：如图2，连接 由＝ ‎ 作垂足为，‎ 则 方法二：如图3，过点作分别交于点，过点 作于点，‎ 是等边三角形 四边形是矩形 在中，‎ A F C E B D O M H G 在中，‎ 在中，‎ ‎ ‎ A F C E B D O M G N ‎（2）结论2成立．‎ 证明：方法一：如图４，过顶点依次作边的垂线围成由（1）得为等边三角形且 过点分别作于,于于点于点 由结论1得： ‎ 又 四边形为矩形 同理：，‎ 方法二：（同结论1方法二的辅助线）‎ A F C E B D ‎（图3）‎ O M H G 在中，‎ 在中，‎ 同理：‎ ‎＝‎ ‎＝‎ 由结论1得：‎ A F C E B D ‎（图5）‎ O 方法三：如图5，连接，根据勾股定理得：‎ ‎：‎ 整理得：‎ ‎ 12分 ‎20．(2009年南充)如图8，半圆的直径，点C在半圆上，．‎ ‎（1）求弦的长；‎ ‎（2）若P为AB的中点，交于点E，求的长．‎ P B C E A ‎【关键词】圆的性质，三角形相似的性质 ‎【答案】解：是半圆的直径，点在半圆上，‎ ‎．‎ 在中， ‎ ‎（2），‎ ‎．，‎ ‎．‎ 又，‎ ‎，‎ ‎．‎ ‎19．(2009年湖州)如图，在平面直角坐标系中，直线∶＝分别与轴，轴相交于两点，点是轴的负半轴上的一个动点，以为圆心，3为半径作．‎ ‎（1）连结，若，试判断与轴的位置关系，并说明理由；‎ ‎（2）当为何值时，以与直线的两个交点和圆心为顶点的三角形是正三角形？‎ B A O x l y P A O x l y ‎（备用图）‎ ‎【关键词】直线与圆的位置关系，相切的判定，正三角形的性质，相似的性质 ‎【答案】‎ 第（1）题 B A O x l y P B A O x l y C E D P1‎ P2‎ 第（2）题 解：（1）与轴相切．‎ 直线与轴交于，与轴交于，‎ ‎，‎ 由题意，．‎ 在中，，‎ 等于的半径，与轴相切． ‎ ‎（2）设与直线交于两点，连结．‎ 当圆心在线段上时，作于．‎ 为正三角形，．‎ ‎，‎ 即，‎ ‎，‎ ‎．‎ 当圆心在线段延长线上时，同理可得，‎ ‎，‎ ‎ 当或时，以与直线的两个交点和圆心为顶点的三角形是正三角形．‎ ‎20．(2009年湖州)若P为所在平面上一点，且，则点叫做的费马点．‎ ‎（1）若点为锐角的费马点，且，则的值为________；‎ ‎（2）如图，在锐角外侧作等边′连结′．‎ 求证：′过的费马点，且′＝．‎ A C B ‎【关键词】阅读理解题，等边三角形的性质，全等三角形的判定及性质，综合题 ‎【答案】（1）2． ‎ ‎（2）‎ A C B P E 证明：在上取点，使，‎ 连结，再在上截取，连结．‎ ‎，‎ 为正三角形，‎ ‎＝，‎ 为正三角形，‎ ‎＝，‎ ‎＝，‎ ‎′，‎ ‎．‎ ‎，‎ ‎，‎ 为的费马点，‎ 过的费马点，且＝+．‎ ‎21．(2009年温州)如图，在△ABC中，∠C＝90°，AC＝3，BC＝4．0为BC边上一点，以0为圆心，OB为半径作半圆与BC边和AB边分别交于点D、点E，连结DE． ’‎ ‎ (1)当BD＝3时，求线段DE的长；‎ ‎ (2)过点E作半圆O的切线，当切线与AC边相交时，设交点为F．求证：△FAE是等腰三角形．‎ ‎【关键词】直角三角形、圆的性质，相似的判定，切线的性质，等腰三角形的判定 ‎【答案】解：（1）∵∠C＝90°，AC＝3，BC＝4，‎ ‎∴AB＝5，‎ ‎∵DB为直径，‎ ‎∴∠DEB＝∠C＝90°，‎ 又∵∠B＝∠B ，∴△DBE∽△ABC ‎∴ 即 ‎∴DE＝。‎ ‎（2）解法一：连结OE，‎ ‎∵EF为半圆O的切线，‎ ‎∴∠DEO+∠DEF＝90°，‎ ‎∵∠AEF+∠DEF＝90°，‎ ‎∴∠AEF＝∠DEO，‎ ‎∵△DBE∽△ABC，‎ ‎∴∠A＝∠EDB，‎ 又∵∠EDO＝∠DEO，‎ ‎∴∠AEF＝∠A，‎ ‎∴△FAE是等腰三角形。‎ 解法二：连结OE，‎ ‎∵EF为半圆O的切线，‎ ‎∴∠AEF+∠OEB＝90°，‎ ‎∵∠C＝90°，‎ ‎∴∠A+∠B＝90°，‎ ‎∵OE＝OB ‎∴∠OEB＝∠B，‎ ‎∴∠AEF＝∠A ‎∴△FAE是等腰三角形。‎ ‎22．（2009临沂）如图，A，B是公路l（l为东西走向）两旁的两个村庄，A村到公路l的距离AC＝1km，B村到公路l的距离BD＝2km，B村在A村的南偏东方向上．‎ ‎（1）求出A，B两村之间的距离；‎ ‎（2）为方便村民出行，计划在公路边新建一个公共汽车站P，要求该站到两村的距离相等，请用尺规在图中作出点P的位置（保留清晰的作图痕迹，并简要写明作法）．‎ 北 东 B A C D l ‎【关键词】等腰直角三角形的性质，勾股定理，尺规作图 ‎【答案】解：（1）方法一：设与的交点为，根据题意可得．‎ 和都是等腰直角三角形．‎ ‎，．‎ 两村的距离为（km）．‎ 方法二：过点作直线的平行线交的延长线于．‎ 易证四边形是矩形，‎ ‎．‎ 在中，由，可得．‎ ‎（km）‎ 两村的距离为km．‎ ‎（2）作图正确，痕迹清晰．‎ B A C D l N M O P 作法：①分别以点为圆心，以大于的长为 半径作弧，两弧交于两点，‎ 作直线；‎ ‎②直线交于点，点即为所求．‎ ‎1．（2009年中山）如图所示，是等边三角形， 点是的中点，延长到，使，‎ ‎（1）用尺规作图的方法，过点作，垂足是（不写作法，保留作图痕迹）；‎ ‎（2）求证：．‎ ‎【关键词】等腰三角形，等边三角形 ‎【答案】解：（1）作图见下图，‎ A C B D E M ‎（2）是等边三角形，是的中点，‎ 平分（三线合一），‎ ‎．‎ ‎，‎ ‎．‎ 又，‎ ‎．‎ 又，‎ ‎，‎ ‎，‎ ‎．‎ 又，‎ ‎．‎ ‎23．（2009年牡丹江）有一块直角三角形的绿地，量得两直角边长分别为 现在要将绿地扩充成等腰三角形，且扩充部分是以为直角边的直角三角形，求扩充后等腰三角形绿地的周长．‎ ‎【关键词】等腰三角形，勾股定理 ‎【答案】在中，‎ 由勾股定理有：，扩充部分为扩充成等腰应分以下三种情况．‎ ‎ ①如图1，当时，可求 ‎ 得的周长为32m．‎ ‎②如图2，当时，可求 由勾股定理得：，得的周长为 ‎③如图3，当为底时，设则 由勾股定理得：，得的周长为 A D C B A D B C A D B C 图1‎ 图2‎ 图3‎ ‎24．(2009年宁德市)（本题满分13分）如图，已知抛物线C1：的顶点为P，与x轴相交于A、B两点（点A在点B的左边），点B的横坐标是1．‎ ‎（1）求P点坐标及a的值；（4分）‎ ‎（2）如图（1），抛物线C2与抛物线C1关于x轴对称，将抛物线C2向右平移，平移后的抛物线记为C3，C3的顶点为M，当点P、M关于点B成中心对称时，求C3的解析式；（4分）‎ ‎（3）如图（2），点Q是x轴正半轴上一点，将抛物线C1绕点Q旋转180°后得到抛物线C4．抛物线C4的顶点为N，与x轴相交于E、F两点（点E在点F的左边），当以点P、N、F为顶点的三角形是直角三角形时，求点Q的坐标．（5分）‎ y x A O B P N 图2‎ C1‎ C4‎ Q E F 图（2）‎ y x A O B P M 图1‎ C1‎ C2‎ C3‎ 图（1）‎ ‎【关键词】二次函数,勾股定理的运用 y x A O B P M 图(1)‎ C1‎ C2‎ C3‎ H G 解：（1）由抛物线C1：得 顶点P的为（-2，-5） ‎ ‎∵点B（1，0）在抛物线C1上 ‎∴‎ ‎ 解得，a＝ ‎ ‎（2）连接PM，作PH⊥x轴于H，作MG⊥x轴于G ‎∵点P、M关于点B成中心对称 ‎∴PM过点B，且PB＝MB ‎∴△PBH≌△MBG ‎∴MG＝PH＝5，BG＝BH＝3‎ ‎∴顶点M的坐标为（4，5） ‎ ‎ 抛物线C2由C1关于x轴对称得到，抛物线C3由C2平移得到 ‎∴抛物线C3的表达式为 ‎ ‎（3）∵抛物线C4由C1绕点x轴上的点Q旋转180°得到 ‎∴顶点N、P关于点Q成中心对称 ‎ 由（2）得点N的纵坐标为5‎ 设点N坐标为（m，5） ‎ y x A O B P N 图(2)‎ C1‎ C4‎ Q E F H G K ‎ ‎ ‎ 作PH⊥x轴于H，作NG⊥x轴于G ‎ 作PK⊥NG于K ‎ ∵旋转中心Q在x轴上 ‎∴EF＝AB＝2BH＝6‎ ‎ ∴FG＝3，点F坐标为（m+3，0）‎ ‎ H坐标为（2，0），K坐标为（m，-5），‎ 根据勾股定理得 ‎ PN2＝NK2+PK2＝m2+4m+104‎ ‎ PF2＝PH2+HF2＝m2+10m+50‎ ‎ NF2＝52+32＝34 ‎ ‎ ①当∠PNF＝90º时，PN2+ NF2＝PF2，解得m＝，∴Q点坐标为（，0） ‎ ‎②当∠PFN＝90º时，PF2+ NF2＝PN2，解得m＝，∴Q点坐标为（，0）‎ ‎③∵PN＞NK＝10＞NF，∴∠NPF≠90º 综上所得，当Q点坐标为（，0）或（，0）时，以点P、N、F为顶点 的三角形是直角三角形． ‎ ‎25．(2009年河北)图10是一个半圆形桥洞截面示意图，圆心为O，直径AB是河底线，弦CD是水位线，CD∥AB，且CD ＝ 24 m，‎ OE⊥CD于点E．已测得sin∠DOE ＝ ．‎ ‎（1）求半径OD；‎ ‎（2）根据需要，水面要以每小时0．5 m的速度下降，则经过多长时间才能将水排干？‎ A O B 图10‎ E C D ‎ ‎ ‎【关键词】解直角三角形,勾股定理,‎ 解：（1）∵OE⊥CD于点E，CD＝24，‎ ‎∴ED ＝＝12．‎ ‎ 在Rt△DOE中，‎ ‎∵sin∠DOE ＝ ＝，‎ ‎∴OD ＝13（m）． ‎ ‎ （2）OE＝‎ ‎＝．‎ ‎ ∴将水排干需：‎ ‎5÷0．5＝10（小时）． ‎ ‎26．(2009年潍坊)在四边形中，，且．取的中点，连结．‎ ‎（1）试判断三角形的形状；‎ ‎（2）在线段上，是否存在点，使．若存在，请求出的长；若不存在，请说明理由．‎ P D C B A 解：（1）在四边形中，，，‎ 四边形为直角梯形（或矩形）．‎ 过点作，垂足为，，‎ 又点是的中点，点是的中点，‎ 又，‎ ‎， ‎ 与是全等的等腰直角三角形，‎ ‎，‎ 是等腰直角三角形． ‎ ‎（2）存在点使． ‎ 以为直径，为圆心作圆．‎ 当时，四边形为矩形，，‎ 圆与相切于点，此时，点与点重合，存在点，使得，‎ 此时． ‎ 当时，四边形为直角梯形，‎ ‎，，圆心到的距离小于圆的半径，圆与相交，上存在两点，使， ‎ 过点作，在中，，‎ 连结，则，‎ 在直角三角形中，，‎ ‎．‎ 同理可得：．‎ 综上所述，在线段上存在点，使．‎ 当时，有一点，；当时，有两点，． ‎ P D C B A Q E M2‎ M1‎ ‎27．（09湖北宜昌）已知：如图， AF平分∠BAC，BC⊥AF， 垂足为E，点D与点A关于点E对称，PB分别与线段CF， AF相交于P，M．‎ ‎(1)求证：AB＝CD；‎ ‎(2)若∠BAC＝2∠MPC，请你判断∠F与∠MCD 的数量关系，并说明理由． ‎ ‎【关键词】全等三角形的性质与判定、等腰三角性的性质 ‎【答案】解：(1)证明：∵AF平分∠BAC， ‎ ‎ ∴∠CAD＝∠DAB＝∠BAC．‎ ‎∵D与A关于E对称，∴E为AD中点．‎ ‎∵BC⊥AD，∴BC为AD的中垂线，∴AC＝CD． ‎ 在Rt△ACE和Rt△ABE中，注：证全等也可得到AC＝CD ‎∠CAD+∠ACE＝∠DAB+∠ABE＝90°， ∠CAD＝∠DAB．‎ ‎∴∠ACE＝∠ABE，∴AC＝AB． 注：证全等也可得到AC＝AB ‎∴AB＝CD． ‎ ‎ ‎ ‎(2)∵∠BAC＝2∠MPC， 又∵∠BAC＝2∠CAD，∴∠MPC＝∠CAD．‎ ‎∵AC＝CD，∴∠CAD＝∠CDA， ∴∠MPC＝∠CDA． ‎ ‎∴∠MPF＝∠CDM． ‎ ‎∵AC＝AB，AE⊥BC，∴CE＝BE． 注：证全等也可得到CE＝BE ‎∴AM为BC的中垂线，∴CM＝BM． 注：证全等也可得到CM＝BM ‎∵EM⊥BC，∴EM平分∠CMB，(等腰三角形三线合一) ‎ ‎∴∠CME＝∠BME． 注：证全等也可得到∠CME＝∠BME ‎ ‎∵∠BME＝∠PMF，‎ ‎∴∠PMF＝∠CME， ‎ ‎∴∠MCD＝∠F(三角形内角和)． 注：证三角形相似也可得到∠MCD＝∠F ‎28．（09湖南怀化）如图12，在直角梯形OABC中， OA∥CB，A、B两点的坐标分别为A（15，0），B（10，12），动点P、Q分别从O、B两点出发，点P以每秒2个单位的速度沿OA向终点A运动，点Q以每秒1个单位的速度沿BC向C运动，当点P停止运动时，点Q也同时停止运动．线段OB、PQ相交于点D，过点D作DE∥OA，交AB于点E，射线QE交轴于点F．设动点P、Q运动时间为t（单位：秒）．‎ ‎（1）当t为何值时，四边形PABQ是等腰梯形，请写出推理过程；‎ ‎（2）当t＝2秒时，求梯形OFBC的面积；‎ ‎（3）当t为何值时，△PQF是等腰三角形？请写出推理过程．‎ ‎【关键词】一元二次方程解法及应用、勾股定理及逆定理、等腰三角形、等腰梯形的判定 ‎【答案】‎ 解：（1）如图4，过B作 则 过Q作 则 要使四边形PABQ是等腰梯形，则，‎ 即 或（此时是平行四边形，不合题意，舍去）‎ ‎（2）当时，。‎ ‎（3）①当时，则 ‎②当时，‎ 即 ‎③当时， ‎ 综上，当时，△PQF是等腰三角形． ‎ ‎29．（09湖南邵阳）如图，在梯形中，，，，将延长至点，使．‎ ‎（1）求的度数；‎ ‎（2）求证：为等腰三角形．‎ D A F B C ‎【关键词】等腰三角性的性质与判定、等腰梯形的性质 ‎【答案】（1）‎ ‎．‎ 在中，‎ ‎；‎ ‎（2）连接．在梯形中，，，‎ 在四边形中，‎ 四边形是平行四边形，，‎ ‎，即为等腰三角形．‎ ‎【关键词】直角三角形的有关计算、勾股定理 ‎【答案】C ‎30．（2009年湖北十堰市）如图，在一次数学课外活动中，小明同学在点P处测得教学楼A位于北偏东60°方向，办公楼B位于南偏东45°方向．小明沿正东方向前进60米到达C处，此时测得教学楼A恰好位于正北方向，办公楼B正好位于正南方向．求教学楼A与办公楼B之间的距离（结果精确到0．1米）．‎ ‎（供选用的数据：≈1．414，≈1．732）‎ ‎【关键词】直角三角形的有关计算、测量问题、勾股定理 ‎【答案】解：由题意可知 ‎ ∠ACP＝ ∠BCP＝ 90°，∠APC＝30°，∠BPC＝45°…2分 在Rt△BPC中，∵∠BCP＝90°，∠BPC＝45°，∴‎ 在Rt△ACP中，∵∠ACP＝90°，∠APC＝30°，∴ ‎ ‎∴‎ ‎≈60+20×1．732 ＝94．64≈94．6(米) ‎ 答：教学楼A与办公楼B之间的距离大约为94．6米．‎ 说明：（1）其它解法请参照上述评分说明给分；（2）不作答不扣分．‎ ‎31．(2009年达州)如图10，⊙O的弦AD∥BC,过点D的切线交BC的延长线于点E，AC∥DE交BD于点H，DO及延长线分别交AC、BC于点G、F．‎ ‎(1)求证：DF垂直平分AC；‎ ‎（2）求证：FC＝CE；‎ ‎（3）若弦AD＝5㎝，AC＝8㎝，求⊙O的半径． ‎ ‎【关键词】圆,平行四边形,勾股定理 ‎【答案】‎ ‎（1）∵DE是⊙O的切线，且DF过圆心O ‎∴DF⊥DE 又∵AC∥DE ‎∴DF⊥AC ‎∴DF垂直平分AC ‎ ‎（2）由（1）知：AG＝GC 又∵AD∥BC ‎∴∠DAG＝∠FCG 又∵∠AGD＝∠CGF ‎∴△AGD≌△CGF（ASA）‎ ‎∴AD＝FC ‎∵AD∥BC且AC∥DE ‎∴四边形ACED是平行四边形 ‎∴AD＝CE ‎∴FC＝CE5分 ‎（3）连结AO； ∵AG＝GC，AC＝8cm，∴AG＝4cm 在Rt△AGD中，由勾股定理得 GD＝AD2-AG2＝52-42＝3cm ‎ 设圆的半径为r，则AO＝r，OG＝r-3‎ 在Rt△AOG中，由勾股定理得 AO2＝OG2+AG2‎ 有：r2＝(r-3)2+42解得 r＝256 ‎ ‎∴⊙O的半径为256cm．‎ ‎32．（2009年广东省）如图所示，是等边三角形，点是的中点，延长到，使．‎ ‎（1）用尺规作图的方法，过点作，垂足是（不写作法，保留作图痕迹）；‎ ‎（2）求证：．‎ A B C E D ‎【关键词】等边三角形；线段和角的概念、性质、画法及有关计算 ‎【答案】解：（1）作图如下图，‎ A B E D C M ‎（2）是等边三角形，是的中点 平分（三线合一），‎ ‎，‎ ‎，‎ ‎，‎ 又 ‎，‎ 又，‎ ‎，‎ ‎，‎ ‎，‎ 又，‎ ‎33．（2009 黑龙江大兴安岭）在边长为4和6的矩形中作等腰三角形，使等腰三角形的一条边是矩形的长或宽，第三个顶点在矩形的边上，求所作三角形的面积．‎ ‎（注：形状相同的三角形按一种计算．）‎ ‎【关键词】等腰三角形 ‎【答案】． 面积是12,面积是8和12‎ ‎34．（2009年崇左）如图，在等腰梯形中，已知，，延长到，使．‎ ‎（1）证明：；‎ D A B E C F ‎（第24题）‎ ‎（2）如果，求等腰梯形的高的值．‎ ‎【关键词】在等腰梯形性质进行转化。‎ ‎【答案】‎ ‎（1）证明：．‎ 又四边形是等腰梯形，，‎ ‎．‎ ‎．‎ ‎（2）四边形是平行四边形，‎ ‎．‎ ‎．‎ 由（1）可知，，．‎ 所以，是等腰直角三角形，即，‎ ‎．‎ 四边形是等腰梯形，而，‎ ‎．‎ ‎．‎ ‎（2009龙岩）阅读下列材料：‎ 正方形网格中，每个小正方形的顶点称为格点，以格点为顶点的三角形叫格点三角形．‎ 数学老师给小明同学出了一道题目：在图正方形网格（每个小正方形边长为1）中画出格点△ABC，使，；‎ 小明同学的做法是：由勾股定理，得，，于是画出线段AB、AC、BC，从而画出格点△ABC．‎ ‎（1）请你参考小明同学的做法，在图23－2正方形网格（每个小正方形边长为1）中画出格点△（点位置如图所示），使＝＝5，．（直接画出图形，不写过程）；‎ ‎（2）观察△ABC与△的形状，猜想∠BAC与∠有怎样的数量关系，并证明你的猜想．‎ C B A ‎【关键词】等腰三角形 ‎【答案】（1）正确画出△‎ ‎（画出其中一种情形即可）‎ ‎ （2）猜想：∠BAC ＝∠ ‎ 证明：∵，；‎ ‎∴，‎ ‎∴△ABC ∽ △，‎ ‎∴∠BAC ＝∠ ‎