【数学】2019届高考一轮复习北师大版理12-2算法与程序框图学案

【数学】2019届高考一轮复习北师大版理12-2算法与程序框图学案

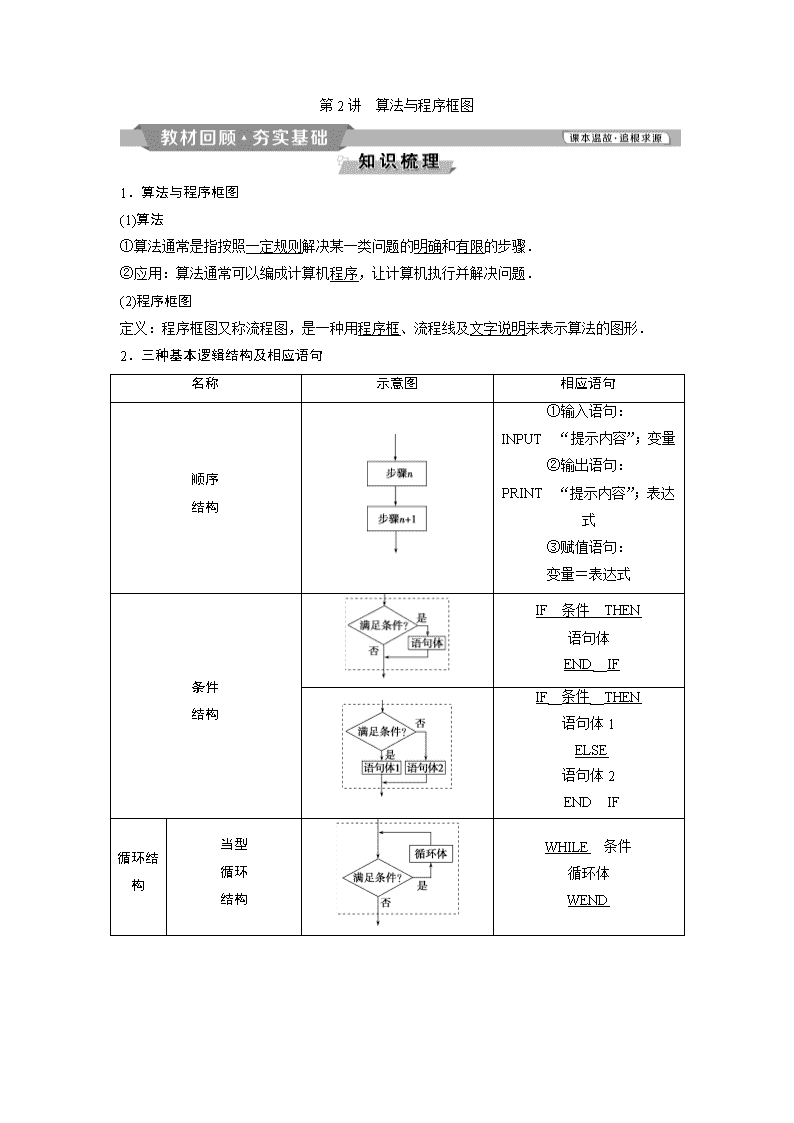
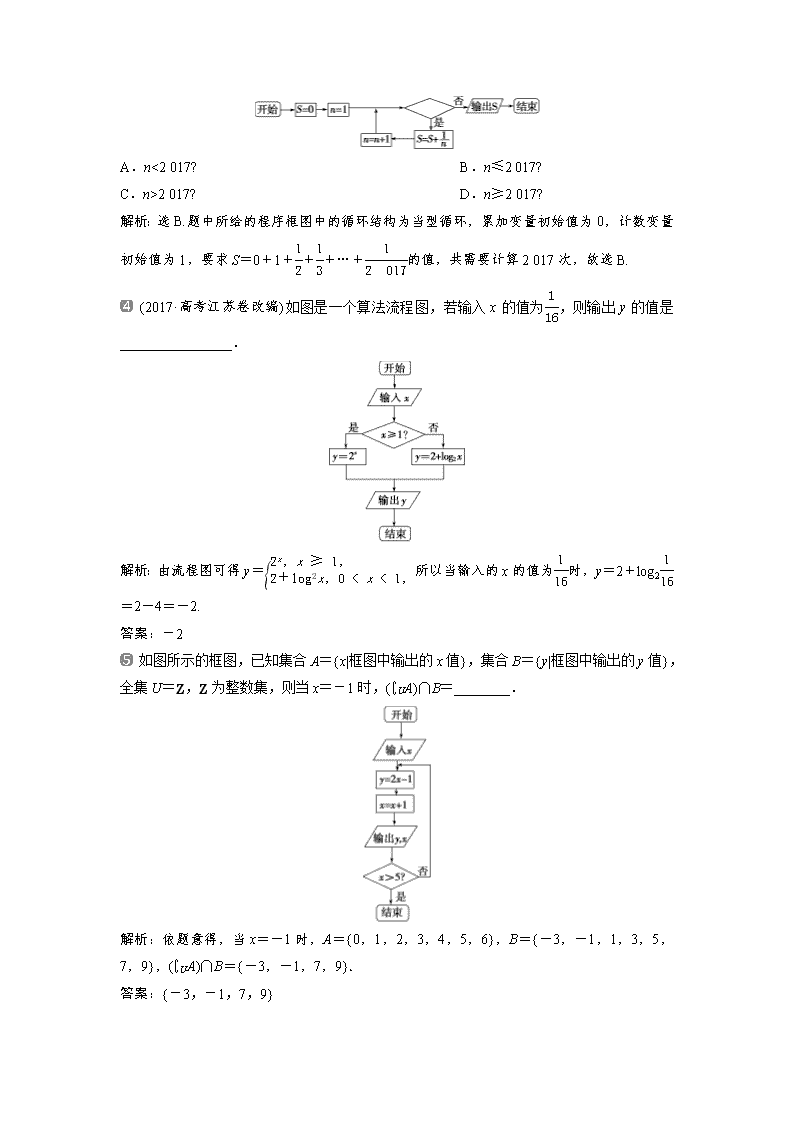
第2讲　算法与程序框图 ‎1．算法与程序框图 ‎(1)算法 ‎①算法通常是指按照一定规则解决某一类问题的明确和有限的步骤．‎ ‎②应用：算法通常可以编成计算机程序，让计算机执行并解决问题．‎ ‎(2)程序框图 定义：程序框图又称流程图，是一种用程序框、流程线及文字说明来表示算法的图形．‎ ‎2．三种基本逻辑结构及相应语句 名称 示意图 相应语句 顺序 结构 ‎①输入语句：‎ INPUT　“提示内容”；变量 ‎②输出语句：‎ PRINT　“提示内容”；表达式 ‎③赋值语句：‎ 变量＝表达式 条件 结构 IF__条件__THEN 语句体 ‎ END__IF IF__条件__THEN 语句体1‎ ‎ ELSE 语句体2‎ ‎ END　IF 循环结构 当型 循环 结构 WHILE　条件 循环体 WEND 直到 型循 环结 构 DO 循环体 LOOP__UNTIL条件 ‎ 判断正误(正确的打“√”，错误的打“×”)‎ ‎(1)一个程序框图一定包含顺序结构，但不一定包含条件结构和循环结构．(　　)‎ ‎(2)条件结构的出口有两个，但在执行时，只有一个出口是有效的．(　　)‎ ‎(3)输入框只能紧接开始框，输出框只能紧接结束框．(　　)‎ ‎(4)输入语句可以同时给多个变量赋值．(　　)‎ ‎(5)在算法语句中，x＝x＋1是错误的．(　　)‎ 答案：(1)√　(2)√　(3)×　(4)√　(5)×‎ ‎ (2017·高考北京卷)执行如图所示的程序框图，输出的s值为(　　)‎ A．2　　　　　　　　　　 B. C. D. 解析：选C.运行该程序，k＝0，s＝1，k<3；‎ k＝0＋1＝1，s＝＝2，k<3；‎ k＝1＋1＝2，s＝＝，k<3；‎ k＝1＋2＝3，s＝＝，k＝3.输出的s值为.故选C.‎ ‎ 要计算1＋＋＋…＋的结果，下面程序框图中的判断框内可以填(　　)‎ A．n<2 017? B．n≤2 017?‎ C．n>2 017? D．n≥2 017?‎ 解析：选B.题中所给的程序框图中的循环结构为当型循环，累加变量初始值为0，计数变量初始值为1，要求S＝0＋1＋＋＋…＋的值，共需要计算2 017次，故选B.‎ ‎ (2017·高考江苏卷改编)如图是一个算法流程图，若输入x的值为，则输出y的值是________________．‎ 解析：由流程图可得y＝所以当输入的x的值为时，y＝2＋log2＝2－4＝－2.‎ 答案：－2‎ ‎ 如图所示的框图，已知集合A＝{x|框图中输出的x值}，集合B＝{y|框图中输出的y值}，全集U＝Z，Z为整数集，则当x＝－1时，(∁UA)∩B＝________．‎ 解析：依题意得，当x＝－1时，A＝{0，1，2，3，4，5，6}，B＝{－3，－1，1，3，5，7，9}，(∁UA)∩B＝{－3，－1，7，9}．‎ 答案：{－3，－1，7，9}‎ 顺序结构与条件结构 ‎ [典例引领]‎ ‎ 执行如图所示的程序框图，如果输入的t∈[－1，3]，则输出的s属于(　　)‎ A．[－3，4]　　　　　　 B．[－5，2]‎ C．[－4，3] D．[－2，5]‎ ‎【解析】　由程序框图得分段函数s＝所以当－1≤t<1时，s＝3t∈[－3，3)；当1≤t≤3时，s＝4t－t2＝－(t－2)2＋4，所以此时3≤s≤4.综上函数的值域为[－3，4]，即输出的s属于[－3，4]．‎ ‎【答案】　A ‎1．若本例的判断框中的条件改为“t≥1？”，则输出的s的范围是________．‎ 解析：由程序框图得分段函数s＝所以当1≤t≤3时，s＝3t∈[3，9]，当－1≤t<1时，s＝4t－t2＝－(t－2)2＋4，所以此时－5≤s<3.综上函数的值域为[－5，9]，即输出的s属于[－5，9]．‎ 答案：[－5，9]‎ ‎2．本例框图不变，若输出s的值为3，求输入的t的值．‎ 解：由本例解析知s＝，‎ 则3t＝3，所以t＝1(舍)，‎ ‎4t－t2＝3，所以t＝1或3.‎ 应用顺序结构和条件结构的注意点 ‎(1)顺序结构 顺序结构是最简单的算法结构，语句与语句之间、框与框之间是按从上到下的顺序进行的．‎ ‎(2)条件结构 利用条件结构解决算法问题时，重点是判断框，判断框内的条件不同，对应的下一图框中的内容和操作要相应地进行变化，故要重点分析判断框内的条件是否满足．‎ ‎[提醒]　条件结构的运用与数学的分类讨论有关．设计算法时，哪一步要分类讨论，哪一步就需要用条件结构．　 ‎ ‎[通关练习]‎ ‎1．阅读如图所示的程序框图，若输入x为3，则输出的y的值为(　　)‎ A．24 B．25‎ C．30 D．40‎ 解析：选D.a＝32－1＝8，b＝8－3＝5，y＝8×5＝40.‎ ‎2．给出一个如图所示的程序框图，若要使输入的x值与输出的y值相等，则这样的x值的个数是(　　)‎ A．1 B．2‎ C．3 D．4‎ 解析：选C.由程序框图知y＝ 由已知得或或 解得x＝0或x＝1或x＝3，‎ 这样的x值的个数是3.‎ 循环结构(高频考点)‎ 循环结构是高考命题的一个热点问题，多以选择题、填空题的形式呈现，试题难度不大，多为容易题或中档题．高考对循环结构的考查主要有以下三个命题角度：‎ ‎(1)由程序框图求输出的结果或输入的值；‎ ‎(2)完善程序框图；‎ ‎(3)辨析程序框图的功能．‎ ‎ [典例引领]‎ ‎ 角度一　由程序框图求输出的结果或输入的值 ‎ (1)(2017·高考全国卷Ⅱ)执行如图的程序框图，如果输入的a＝－1，则输出的S＝(　　)‎ A．2 B．3‎ C．4 D．5‎ ‎(2)(2017·高考全国卷Ⅲ)执行如图的程序框图，为使输出S的值小于91，则输入的正整数N的最小值为(　　)‎ A．5 B．4‎ C．3 D．2‎ ‎【解析】　(1)运行程序框图，a＝－1，S＝0，K＝1，K≤6成立；S＝0＋(－1)×1＝－1，a＝1，K＝2，K≤6成立；S＝－1＋1×2＝1，a＝－1，K＝3，K≤6成立；S＝1＋(－1)×3＝－2，a＝1，K＝4，K≤6成立；S＝－2＋1×4＝2，a＝－1，K＝5，K≤6成立；S＝2＋(－1)×5＝－3，a＝1，K＝6，K≤6成立；S＝－3＋1×6＝3，a＝－1，K＝7，K≤6不成立，输出S＝3.选择B.‎ ‎(2)S＝0＋100＝100，M＝－10，t＝2，100>91；S＝100－10＝90，M＝1，t＝3，90<91，输出S，此时，t＝3不满足t≤N，所以输入的正整数N的最小值为2，故选D.‎ ‎【答案】　(1)B　(2)D 角度二　完善程序框图 ‎ (2017·高考全国卷Ⅰ)如图程序框图是为了求出满足3n－2n>1 000的最小偶数n，那么在和两个空白框中，可以分别填入(　　)‎ A．A>1 000和n＝n＋1‎ B．A>1 000和n＝n＋2‎ C．A≤1 000和n＝n＋1‎ D．A≤1 000和n＝n＋2‎ ‎【解析】　程序框图中A＝3n－2n，故判断框中应填入A≤1 000，由于初始值n＝0，要求满足A＝3n－2n>1 000的最小偶数，故执行框中应填入n＝n＋2，选D.‎ ‎【答案】　D 角度三　辨析程序框图的功能 ‎ 如图所示的程序框图，该算法的功能是(　　)‎ A．计算(1＋20)＋(2＋21)＋(3＋22)＋…＋(n＋1＋2n)的值 B．计算(1＋21)＋(2＋22)＋(3＋23)＋…＋(n＋2n)的值 C．计算(1＋2＋3＋…＋n)＋(20＋21＋22＋…＋2n－1)的值 D．计算[1＋2＋3＋…＋(n－1)]＋(20＋21＋22＋…＋2n)的值 ‎【解析】　初始值k＝1，S＝0，第1次进入循环体时，S＝1＋20，k＝2；当第2次进入循环体时，S＝1＋20＋2＋21，k＝3，…；给定正整数n，当k＝n时，最后一次进入循环体，则有S＝1＋20＋2＋21＋…＋n＋2n－1，k＝n＋1，终止循环体，输出S＝(1＋2＋3＋…＋n)＋(20＋21＋22＋…＋2n－1)，故选C.‎ ‎【答案】　C 与循环结构有关问题的常见类型及解题策略 ‎(1)已知程序框图，求输出的结果，可按程序框图的流程依次执行，最后得出结果．‎ ‎(2)完善程序框图问题，结合初始条件和输出结果，分析控制循环的变量应满足的条件或累加、累乘的变量的表达式．‎ ‎(3)对于辨析程序框图功能问题，可将程序执行几次，即可根据结果作出判断．‎ ‎[提醒]　(1)注意区分当型循环和直到型循环．‎ ‎(2)循环结构中要正确控制循环次数．‎ ‎(3)要注意各个框的顺序．　 ‎ ‎[通关练习]‎ ‎1．(2017·高考天津卷)阅读如图所示的程序框图，运行相应的程序，若输入N的值为24，则输出N的值为(　　)‎ A．0 B．1‎ C．2 D．3‎ 解析：选C.第一次循环，24能被3整除，N＝＝8＞3；第二次循环，8不能被3整除，N＝8－1＝7＞3；第三次循环，7不能被3整除，N＝7－1＝6＞3；第四次循环，6能被3整除，N＝＝2＜3，结束循环，故输出N的值为2.选择C.‎ ‎2．(2018·宝鸡市质量检测(一)) 阅读如图所示的程序框图，运行相应的程序．若输入x的值为1，则输出S的值为(　　)‎ A．64 B．73‎ C．512 D．585‎ 解析：选B.程序框图执行过程如下：x＝1，S＝0，S＝1，S<50⇒x＝2，S＝9，S<50⇒x＝4，S＝73>50，跳出循环，输出S＝73.‎ ‎3．(2018·广东省五校协作体联考)已知函数f(x)＝ax3＋x2在x＝－1处取得极大值，记g(x)＝.执行如图所示的程序框图，若输出的结果S>，则判断框中可以填入的关于n的判断条件是(　　)‎ A．n≤2 016? B．n≤2 017?‎ C．n>2 016? D．n>2 017?‎ 解析：选B.f′(x)＝3ax2＋x，则f′(－1)＝3a－1＝0，解得a＝，g(x)＝＝＝＝－，g(n)＝－，则S＝1－＋－＋…＋－＝1－＝，因为输出的结果S>，分析可知判断框中可以填入的判断条件是“n≤2 017？”，选B.‎ 基本算法语句 ‎ [典例引领]‎ ‎ (1)设计一个计算1×3×5×7×9×11×13的算法，下面给出了程序的一部分，则在①处不能填入的数是(　　)‎ S＝1‎ i＝3‎ WHILE　i<①‎ S＝S*i i＝i＋2‎ WEND PRINT　S END A．13　　　　　　　　　　 B．13.5‎ C．14 D．14.5‎ ‎(2)表示函数y＝f(x)的程序如图所示 INPUT　　x IF　x＞0　THEN y＝1‎ ELSE IF　x＝0　THEN y＝0‎ ELSE y＝－1‎ END　IF END　IF PRINT　　y END 则关于函数y＝f(x)有下列结论：‎ ‎①y＝f(x)的图象关于原点对称．‎ ‎②y＝f(x)的值域为[－1，1]．‎ ‎③y＝f(x)是周期T＝1的周期函数．‎ ‎④y＝f(x)在R上是增函数．‎ ‎⑤函数y＝f(x)－kx(k＞0)有三个零点．‎ 则正确结论的序号为________．(填上所有正确结论的序号)‎ ‎【解析】　(1)若填13，当i＝11＋2＝13时，不满足条件，终止循环，因此得到的是1×3×5×7×9×11的计算结果，故不能填13，但填的数字只要超过13且不超过15时均可保证终止循环，得到的是1×3×5×7×9×11×13的计算结果．‎ ‎(2)由程序知y＝f(x)＝，‎ 其图象如图 图象关于原点对称，①正确；值域为{1，0，－1}，②错误；不是周期函数，在R上也不是增函数，③④错误；当k＞0时，y＝f(x)与y＝kx有三个交点，故⑤正确．‎ ‎【答案】　(1)A　(2)①⑤‎ ‎　 ‎ ‎ 下列程序执行后输出的结果是________．‎ i＝11‎ S＝1‎ DO S＝S*i i＝i－1‎ LOOP UNTIL　i<9‎ PRINT　S END 解析：程序反映出的算法过程为 i＝11⇒S＝11×1，i＝10；i＝10⇒S＝11×10，i＝9；‎ i＝9⇒S＝11×10×9，i＝8；‎ i＝8<9退出循环，执行“PRINT　S”．‎ 故S＝990.‎ 答案：990‎ 算法与其他知识的交汇 ‎ [典例引领]‎ ‎ (1)(2018·湖北荆州七校联考)宋元时期数学名著《算学启蒙》中有关于“松竹并生”的问题：松长五尺，竹长两尺，松日自半，竹日自倍，松竹何日而长等．下图是源于其思想的一个程序框图，若输入的a，b分别为5，2，则输出的n＝(　　)‎ A．2 B．3‎ C．4 D．5‎ ‎(2)执行如图所示的程序框图，如果输入的x，y∈R，那么输出的S的最大值为(　　)‎ A．0 B．1‎ C．2 D．3‎ ‎【解析】　(1)程序运行如下：n＝1，a＝5＋＝，b＝4，a>b，继续循环；‎ n＝2，a＝＋×＝，b＝8，a>b，继续循环；‎ n＝3，a＝＋×＝，b＝16，a>b，继续循环；‎ n＝4，a＝＋×＝，b＝32，此时，a0时，第一次对y赋值为3x＋2，第二次对y又赋值为－x2＋1，最后y＝－x2＋1，于是由－x2＋1＝0，得x＝1，综上知输入的x值为－1或1，故选B.‎ ‎2．(2018·兰州双基过关考试)执行如图所示的程序框图，若输出i的值为2，则输入x的最大值是(　　)‎ A．5　　　　　　　　　 B．6‎ C．11 D．22‎ 解析：选D.执行该程序可知解得即83，终止循环，输出x＝19.‎ ‎4．(2016·高考全国卷Ⅱ)中国古代有计算多项式值的秦九韶算法，如图是实现该算法的程序框图．执行该程序框图，若输入的x＝2，n＝2，依次输入的a为2，2，5，则输出的s＝(　　)‎ A．7 B．12‎ C．17 D．34‎ 解析：选C.由程序框图知，第一次循环：x＝2，n＝2，a＝2，s＝0×2＋2＝2，k＝1；第二次循环：a＝2，s＝2×2＋2＝6，k＝2；第三次循环：a＝5，s＝6×2＋5＝17，k＝3.结束循环，输出s的值为17，故选C.‎ ‎5．执行如图所示的程序框图，若输出k的值为6，则判断框内可填入的条件是(　　)‎ A．s>？ B．s>？‎ C．s>？ D．s>？‎ 解析：选C.第一次执行循环：s＝1×＝，k＝8，s＝应满足条件；第二次执行循环：s＝×＝，k＝7，s＝应满足条件，排除选项D；第三次执行循环：s＝×＝，k＝6，正是输出的结果，故这时程序不再满足条件，结束循环，而选项A和B都满足条件，故排除A和B，故选C.‎ ‎6．(2018·湖南省湘中名校高三联考)执行如图所示的程序框图，如果运行结果为5 040，那么判断框中应填入(　　)‎ A．k<6? B．k<7?‎ C．k>6? D．k>7?‎ 解析：选D.第一次循环，得S＝2，k＝3；第二次循环，得S＝6，k＝4；第三次循环，得S＝24，k＝5；第四次循环，得S＝120，k＝6；第五次循环，得S＝720，k＝7；第六次循环，得S＝5 040，k＝8，此时满足题意，退出循环，输出的S＝5 040，故判断框中应填入“k>7？”，故选D.‎ ‎7．(2018·河南百校联盟模拟)《九章算术》是中国古代数学名著，体现了古代劳动人民的数学智慧，其中有一竹节容量问题，某教师根据这一问题的思想设计了如图所示的程序框图，若输出的m的值为35，则输入的a的值为(　　)‎ A．4 B．5‎ C．7 D．11‎ 解析：选A.起始阶段有m＝2a－3，i＝1，‎ 第一次循环，m＝2(2a－3)－3＝4a－9，i＝2；‎ 第二次循环，m＝2(4a－9)－3＝8a－21，i＝3；‎ 第三次循环，m＝2(8a－21)－3＝16a－45，i＝4；‎ 接着计算m＝2(16a－45)－3＝32a－93，跳出循环，‎ 输出m＝32a－93，令32a－93＝35，得a＝4.‎ ‎8．(2017·高考山东卷)执行两次如图所示的程序框图，若第一次输入的x的值为7，第二次输入的x的值为9，则第一次、第二次输出的a的值分别为(　　)‎ A．0，0 B．1，1‎ C．0，1 D．1，0‎ 解析：选D.当输入x＝7时，b＝2，因为b2＞x不成立且x不能被b整除，故b＝3，这时b2＞x成立，故a＝1，输出a的值为1.当输入x＝9时，b＝2，因为b2＞x不成立且x不能被b整除，故b＝3，这时b2＞x不成立且x能被b整除，故a＝0，输出a的值为0.‎ ‎9．输入x＝5，运行如图所示的程序后得到的y等于________．‎ INPUT　x IF　x<0　THEN y＝(x＋1)*(x＋1)‎ ELSE y＝(x－1)*(x－1)‎ END IF PRINT　y END 解析：由题意，得y＝f(x)＝ 所以f(5)＝(5－1)2＝16.‎ 答案：16‎ ‎10．(2018·石家庄市第一次模拟)程序框图如图，若输入的S＝1，k＝1，则输出的S为____________．‎ 解析：第一次循环，k＝2，S＝4；第二次循环，k＝3，S＝11；第三次循环，k＝4，S＝26；第四次循环，k＝5，S＝57.此时，终止循环，输出的S＝57.‎ 答案：57‎ ‎11．(2018·广州市高考模拟)执行如图所示的程序框图，输出的结果为____________．‎ 解析：第一步：s＝1－1＝0，t＝1＋1＝2，x＝0，y＝2，k＝1＜3；‎ 第二步：s＝－2，t＝2，x＝－2，y＝2，k＝2＜3；‎ 第三步：s＝－4，t＝0，x＝－4，y＝0，k＝3，结束循环．故输出的结果为(－4，0)．‎ 答案：(－4，0)‎ ‎12．执行如图所示的程序框图，输出的T的值为________．‎ 解析：执行第1次，n＝1＜3，T＝1＋∫xdx＝1＋x2|＝1＋＝；n＝2＜3，执行第2次，T＝＋∫x2dx＝＋x3|＝＋＝；n＝3，不满足n＜3，输出T＝.‎ 故输出的T的值为.‎ 答案： ‎1．(2018·新疆乌鲁木齐一诊)执行如图所示的程序框图(n∈N*)，则输出的S＝(　　)‎ A．a＋aq＋…＋aqn－1 B. C．a＋aq＋…＋aqn D. 解析：选C.执行第1次循环体运算，得i＝1，S＝a；‎ 执行第2次循环体运算，得i＝2，S＝a＋aq；‎ ‎…‎ 执行第n＋1次循环体运算，得i＝n＋1，S＝a＋aq＋…＋aqn.故选C.‎ ‎2．(2018·福州市综合质量检测)执行如图所示的程序框图，若输入的m＝168，n＝112，则输出的k，m的值分别为(　　)‎ A．4，7 B．4，56‎ C．3，7 D．3，56‎ 解析：选C.对第一个当型循环结构，第一次循环：k＝1，m＝84，n＝56，m，n均为偶数；第二次循环：k＝2，m＝42，n＝28，m，n均为偶数；第三次循环：k＝3，m＝21，n＝14，因为m不是偶数，所以结束第一个循环．又m≠n，所以执行第二个当型循环结构，第一次循环：d＝|21－14|＝7，m＝14，n＝7，m≠n；第二次循环：d＝|14－7|＝7，m＝7，n＝7，因为m＝n，所以结束循环，输出k＝3，m＝7，故选C.‎ ‎3．一个算法的程序框图如图所示，若输入的值为2 017，则输出的i值为________．‎ 解析：运行程序框图．‎ x＝2 017，a＝2 017，i＝1，b＝ ‎＝，b≠x；‎ i＝2，a＝－，b＝＝，b≠x；‎ i＝3，a＝，‎ b＝＝2 017，b＝x.终止循环，故输出i＝3.‎ 答案：3‎ ‎4．某程序框图如图所示，则该程序运行后输出的S的值为________．‎ 解析：依题意得，运行程序后输出的是数列{an}的第2 017项，其中数列{an}满足：a1＝1，an＋1＝ 注意到a2＝，a3＝，a4＝，a5＝1，a6＝，…，‎ 该数列中的项以4为周期重复性地出现，‎ 且2 017＝4×504＋1，‎ 因此a2 017＝a1＝1，运行程序后输出的S的值为1.‎ 答案：1‎ ‎5．根据如图所示的程序框图，将输出的x，y值依次分别记为x1，x2，…，xn，…，x2 008；y1，y2，…，yn，…，y2 008.‎ ‎(1)求数列{xn}的通项公式xn；‎ ‎(2)写出y1，y2，y3，y4，由此猜想出数列{yn}的一个通项公式yn，并证明你的结论．‎ ‎(3)求zn＝x1y1＋x2y2＋…＋xnyn(n∈N*，n≤2 008)．‎ 解：(1)由框图，知数列{xn}中，x1＝1，xn＋1＝xn＋2，所以xn＝1＋2(n－1)＝2n－1(n∈N*，n≤2 008)．‎ ‎(2)y1＝2，y2＝8，y3＝26，y4＝80.‎ 由此，猜想yn＝3n－1(n∈N*，n≤2 008)．‎ 证明如下：由框图，知数列{yn}中，yn＋1＝3yn＋2，‎ 所以yn＋1＋1＝3(yn＋1)，‎ 所以＝3，y1＋1＝3.‎ 所以数列{yn＋1}是以3为首项，3为公比的等比数列．所以yn＋1＝3·3n－1＝3n，‎ 所以yn＝3n－1(n∈N*，n≤2 008)．‎ ‎(3)zn＝x1y1＋x2y2＋…＋xnyn ‎＝1×(3－1)＋3×(32－1)＋…＋(2n－1)(3n－1)‎ ‎＝1×3＋3×32＋…＋(2n－1)·3n－[1＋3＋…＋(2n－1)]，‎ 记Sn＝1×3＋3×32＋…＋(2n－1)·3n，①‎ 则3Sn＝1×32＋3×33＋…＋(2n－1)×3n＋1，②‎ ‎①－②，得－2Sn＝3＋2·32＋2·33＋…＋2·3n－(2n－1)·3n＋1‎ ‎＝2(3＋32＋…＋3n)－3－(2n－1)·3n＋1‎ ‎＝2×－3－(2n－1)·3n＋1‎ ‎＝3n＋1－6－(2n－1)·3n＋1＝2(1－n)·3n＋1－6，‎ 所以Sn＝(n－1)·3n＋1＋3.‎ 又1＋3＋…＋(2n－1)＝n2，‎ 所以zn＝(n－1)·3n＋1＋3－n2(n∈N*，n≤2 008)．‎