- 2021-02-26 发布 |
- 37.5 KB |
- 11页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2021届高考数学一轮总复习课时作业61变量间的相关关系统计案例含解析苏教版
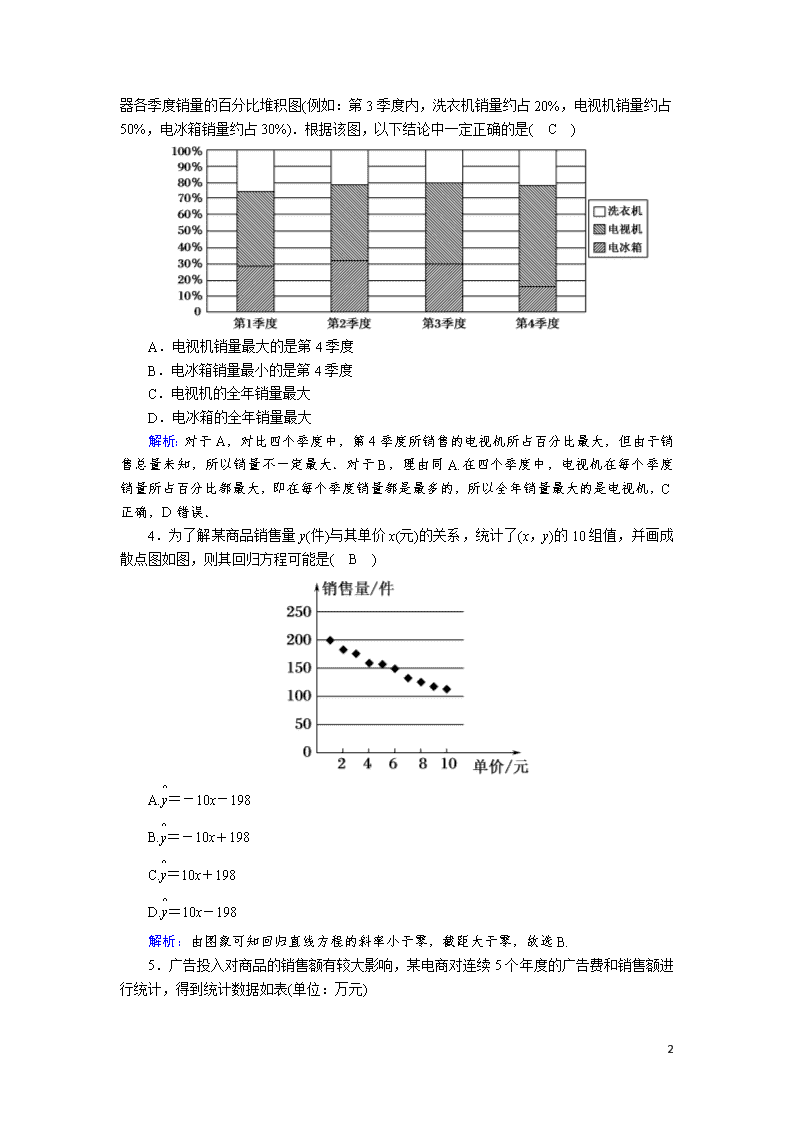
课时作业61 变量间的相关关系、统计案例 一、选择题 1.(2020·昆明市诊断测试)某商家今年上半年各月的人均销售额(单位:千元)与利润率统计表如下: 月份 1 2 3 4 5 6 人均销售额 6 5 8 3 4 7 利润率(%) 12.6 10.4 18.5 3.0 8.1 16.3 根据表中数据,下列说法正确的是( A ) A.利润率与人均销售额成正相关关系 B.利润率与人均销售额成负相关关系 C.利润率与人均销售额成正比例函数关系 D.利润率与人均销售额成反比例函数关系 解析:画出利润率与人均销售额的散点图,如图.由图可知利润率与人均销售额成正相关关系.故选A. 2.下列说法错误的是( B ) A.自变量取值一定时,因变量的取值带有一定随机性的两个变量之间的关系叫做相关关系 B.在线性回归分析中,相关系数r的值越大,变量间的相关性越强 C.在残差图中,残差点分布的带状区域的宽度越狭窄,其模型拟合的精度越高 D.在回归分析中,R2为0.98的模型比R2为0.80的模型拟合的效果好 解析:根据相关关系的概念知A正确;当r>0时,r越大,相关性越强,当r<0时,r越大,相当性越弱,故B不正确;对于一组数据的拟合程度的好坏的评价,一是残差点分布的带状区域越窄,拟合效果越好,二是R2越大,拟合效果越好,所以R2为0.98的模型比R2为0.80的模型拟合的效果好,C、D正确,故选B. 3.(2020·昆明市教学质量检测)下图是某商场 11 2018年洗衣机、电视机和电冰箱三种电器各季度销量的百分比堆积图(例如:第3季度内,洗衣机销量约占20%,电视机销量约占50%,电冰箱销量约占30%).根据该图,以下结论中一定正确的是( C ) A.电视机销量最大的是第4季度 B.电冰箱销量最小的是第4季度 C.电视机的全年销量最大 D.电冰箱的全年销量最大 解析:对于A,对比四个季度中,第4季度所销售的电视机所占百分比最大,但由于销售总量未知,所以销量不一定最大.对于B,理由同A.在四个季度中,电视机在每个季度销量所占百分比都最大,即在每个季度销量都是最多的,所以全年销量最大的是电视机,C正确,D错误. 4.为了解某商品销售量y(件)与其单价x(元)的关系,统计了(x,y)的10组值,并画成散点图如图,则其回归方程可能是( B ) A.=-10x-198 B.=-10x+198 C.=10x+198 D.=10x-198 解析:由图象可知回归直线方程的斜率小于零,截距大于零,故选B. 5.广告投入对商品的销售额有较大影响,某电商对连续5个年度的广告费和销售额进行统计,得到统计数据如表(单位:万元) 11 广告费 2 3 4 5 6 销售额 29 41 50 59 71 由表可得回归方程为=10.2x+,据此模拟,预测广告费为10万元时的销售额约为( C ) A.101.2 B.108.8 C.111.2 D.118.2 解析:由题意得:=4,=50,∴50=4×10.2+,解得=9.2,∴回归直线方程为=10.2x+9.2,∴当x=10时,=10.2×10+9.2=111.2,故选C. 6.某考察团对10个城市的职工人均工资x(千元)与居民人均消费y(千元)进行调查统计,得出y与x具有线性相关关系,且回归方程为=0.6x+1.2.若某城市职工人均工资为5千元,估计该城市人均消费额占人均工资收入的百分比为( D ) A.66% B.67% C.79% D.84% 解析:因为y与x具有线性相关关系,满足回归方程=0.6x+1.2,该城市职工人均工资为x=5,所以可以估计该城市的职工人均消费水平y=0.6×5+1.2=4.2,所以可以估计该城市人均消费额占人均工资收入的百分比为=84%. 7.千年潮未落,风起再扬帆,为实现“两个一百年”奋斗目标、实现中华民族伟大复兴的中国梦奠定坚实基础,某校积极响应国家号召,不断加大拔尖人才的培养力度,据不完全统计: 年份/届 2014 2015 2016 2017 学科竞赛获省级一等奖 及以上的学生人数x 51 49 55 57 被清华、北大等世界名校 录取的学生人数y 103 96 108 107 根据上表可得回归方程=x+中的为1.35,该校2018届同学在学科竞赛中获省级一等奖及以上的学生人数为63,据此模型预测该校今年被清华、北大等世界名校录取的学生人数为( B ) A.111 B.117 C.118 D.123 解析:因为=53,=103.5,所以=-=103.5-1.35×53=31.95,所以回归直线方程为=1.35x+31.95,当x=63时,代入解得=117,故选B. 8.随着国家二孩政策的全面放开,为了调查一线城市和非一线城市的二孩生育意愿,某机构用简单随机抽样方法从不同地区调查了100位育龄妇女,结果如下表. 非一线 一线 总计 愿生 45 20 65 不愿生 13 22 35 11 总计 58 42 100 由K2=, 得K2=≈9.616. 参照下表, P(K2≥k0) 0.050 0.010 0.001 k0 3.841 6.635 10.828 下列说法中,正确的结论是( C ) A.在犯错误的概率不超过0.1%的前提下,认为“生育意愿与城市级别有关” B.在犯错误的概率不超过0.1%的前提下,认为“生育意愿与城市级别无关” C.有99%以上的把握认为“生育意愿与城市级别有关” D.有99%以上的把握认为“生育意愿与城市级别无关” 解析:∵K2≈9.616>6.635,∴有99%以上的把握认为“生育意愿与城市级别有关”. 二、填空题 9.经调查某地若干户家庭的年收入x(万元)和年饮食支出y(万元)具有线性相关关系,并得到y关于x的线性回归直线方程:=0.245x+0.321,由回归直线方程可知,家庭年收入每增加1万元,年饮食支出平均增加0.245万元. 解析:x变为x+1,=0.245(x+1)+0.321=0.245x+0.321+ 0.245,因此家庭年收入每增加1万元,年饮食支出平均增加0.245万元. 10.在一次考试中,5名学生的数学和物理成绩如下表:(已知学生的数学和物理成绩具有线性相关关系) 学生的编号i 1 2 3 4 5 数学成绩x 80 75 70 65 60 物理成绩y 70 66 68 64 62 现已知其线性回归方程为y=0.36x+,则根据此线性回归方程估计数学得90分的同学的物理成绩为73.(四舍五入到整数) 解析:==70, ==66, 所以66=0.36×70+,=40.8, 即线性回归方程为=0.36x+40.8. 当x=90时,=0.36×90+40.8=73.2≈73. 11.已知某次考试之后,班主任从全班同学中随机抽取一个容量为8的样本,他们的数学、物理成绩(单位:分)对应如下表: 11 学生编号 1 2 3 4 5 6 7 8 数学成绩 60 65 70 75 80 85 90 95 物理成绩 72 77 80 84 88 90 93 95 给出散点图如下: 根据以上信息,判断下列结论: ①根据散点图,可以判断数学成绩与物理成绩具有线性相关关系; ②根据散点图,可以判断数学成绩与物理成绩具有一次函数关系; ③从全班随机抽取甲、乙两名同学,若甲同学数学成绩为80分,乙同学数学成绩为60分,则甲同学的物理成绩一定比乙同学的物理成绩高. 其中正确的个数为1. 解析:由散点图知,各点都分布在一条直线附近,故可以判断数学成绩与物理成绩具有线性相关关系,但不能判断数学成绩与物理成绩具有一次函数关系,故①正确,②错误;若甲同学数学成绩为80分,乙同学数学成绩为60分,则甲同学的物理成绩可能比乙同学的物理成绩高,故③错误.综上,正确的个数为1. 12.为了研究工人的日平均工作量是否与年龄有关,从某工厂抽取了100名工人,且规定日平均生产件数不少于80件者为“生产能手”,列出的2×2列联表如下: 生产能手 非生产能手 总计 25周岁以上 25 35 60 25周岁以下 10 30 40 总计 35 65 100 有90%以上的把握认为“工人是否为‘生产能手’与工人的年龄有关”. P(K2≥k) 0.10 0.050 0.010 0.001 k 2.706 3.841 6.635 10.828 解析:由2×2列联表可知, K2=≈2.93, 因为2.93>2.706,所以有90%以上的把握认为“工人是否为‘生产能手’与工人的年龄有关”. 三、解答题 13.(2019·全国卷Ⅰ)某商场为提高服务质量,随机调查了50名男顾客和50名女顾客,每位顾客对该商场的服务给出满意或不满意的评价,得到下面列联表: 11 满意 不满意 男顾客 40 10 女顾客 30 20 (1)分别估计男、女顾客对该商场服务满意的概率; (2)能否有95%的把握认为男、女顾客对该商场 服务的评价有差异? 解:(1)由调查数据知,男顾客中对该商场服务满意的比率为=0.8,因此男顾客对该商场服务满意的概率的估计值为0.8. 女顾客中对该商场服务满意的比率为=0.6,因此女顾客对该商场服务满意的概率的估计值为0.6. (2)K2=≈4.762. 由于4.762>3.841,故有95%的把握认为男、女顾客对该商场服务的评价有差异. 14.(2020·长沙市统考)某互联网公司为了确定下一季度的前期广告投入计划,收集了近6个月广告投入量x(单位:万元)和收益y(单位:万元)的数据如下表: 月份 1 2 3 4 5 6 广告投入量/万元 2 4 6 8 10 12 收益/万元 14.21 20.31 31.8 31.18 37.83 44.67 他们用两种模型①y=bx+a,②y=aebx分别进行拟合,得到相应的回归方程并进行残差分析,得到如图所示的残差图及一些统计量的值: iyi 7 30 1 464.24 364 11 (1)根据残差图,比较模型①,②的似合效果,应选择哪个模型?并说明理由. (2)残差绝对值大于2的数据被认为是异常数据,需要剔除: (ⅰ)剔除异常数据后,求出(1)中所选模型的回归方程; (ⅱ)广告投入量x=18时,(1)中所选模型收益的预报值是多少? 附:对于一组数据(x1,y1),(x2,y2),…,(xn,yn),其回归直线=x+的斜率和截距的最小二乘估计分别为:==,=-. 解:(1)应该选择模型①,因为模型①的残差点比较均匀地落在水平的带状区域中,且模型①的带状区域比模型②的带状区域窄,所以模型①的拟合精度高,回归方程的预报精度高. (2)(ⅰ)剔除异常数据,即3月份的数据后,得 =×(7×6-6)=7.2, =×(30×6-31.8)=29.64. iyi=1 464.24-6×31.8=1 273.44, =364-62=328. ====3, =-=29.64-3×7.2=8.04. 所以y关于x的回归方程为=3x+8.04. (ⅱ)所x=18代入(ⅰ)中所求回归方程得=3×18+8.04=62.04,故预报值为62.04万元. 11 15.(2020·福建省高三检测)“工资条里显红利,个税新政入民心”.随着2019年新年钟声的敲响,我国自1980年以来,力度最大的一次个人所得税(简称个税)改革迎来了全面实施的阶段.某IT从业者为了解自己在个税新政下能享受多少税收红利,绘制了他在26岁~35岁(2009年~2018年)之间各年的月平均收入y(单位:千元)的散点图: (1)由散点图知,可用回归模型y=blnx+a拟合y与x的关系,试根据有关数据建立y关于x的回归方程; (2)如果该IT从业者在个税新政下的专项附加扣除为3 000元/月,试利用(1)的结果,将月平均收入视为月收入,根据新旧个税政策,估计他36岁时每个月少缴纳的个人所得税. 附注:1.参考数据:i=55,i=155.5,(xi-)2=82.5,(xi-)(yi-)=94.9,i=15.1,(ti-)2=4.84,(ti-)(yi-)=24.2,其中ti=ln xi;取ln 11=2.4,ln 36=3.6. 2.参考公式:回归方程v=bu+a中斜率和截距的最小二乘估计分别为=,=-. 3.新旧个税政策下每月应纳税所得额(含税)计算方法及税率表如下: 11 解:(1)令t=ln x,则y=bt+a. ===5, ===15.55,===1.51, =-=15.55-5×1.51=8, 所以y关于t的回归方程为y=5t+8. 因为t=ln x,所以y关于x的回归方程为y=5ln x+8. (2)由(1)得该IT从业者36岁时月平均收入为 y=5ln11+8=5×2.4+8=20(千元). 11 旧个税政策下每个月应缴纳的个人所得税为 1 500×3%+3 000×10%+4 500×20%+(20 000-3 500-9 000)×25%=3 120(元). 新个税政策下每个月应维纳的个人所得部为 3 000×3%+(20 000-5 000-3 000-3 000)×10%=990(元). 故根据新旧个税政策,该IT从业者36岁时每个月少缴纳的个人所得税为3 120-990=2 130(元). 11 11查看更多