- 2021-06-25 发布 |
- 37.5 KB |
- 9页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
上海中考长宁区初三数学二模试卷及答案
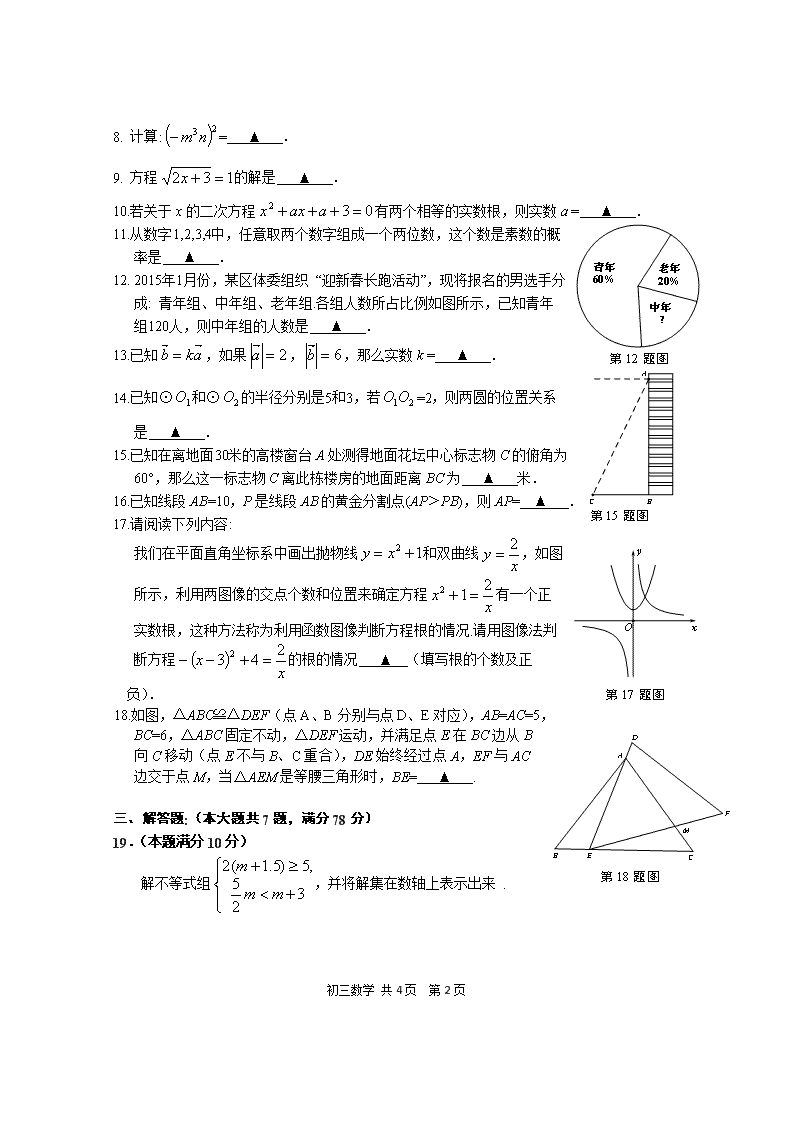
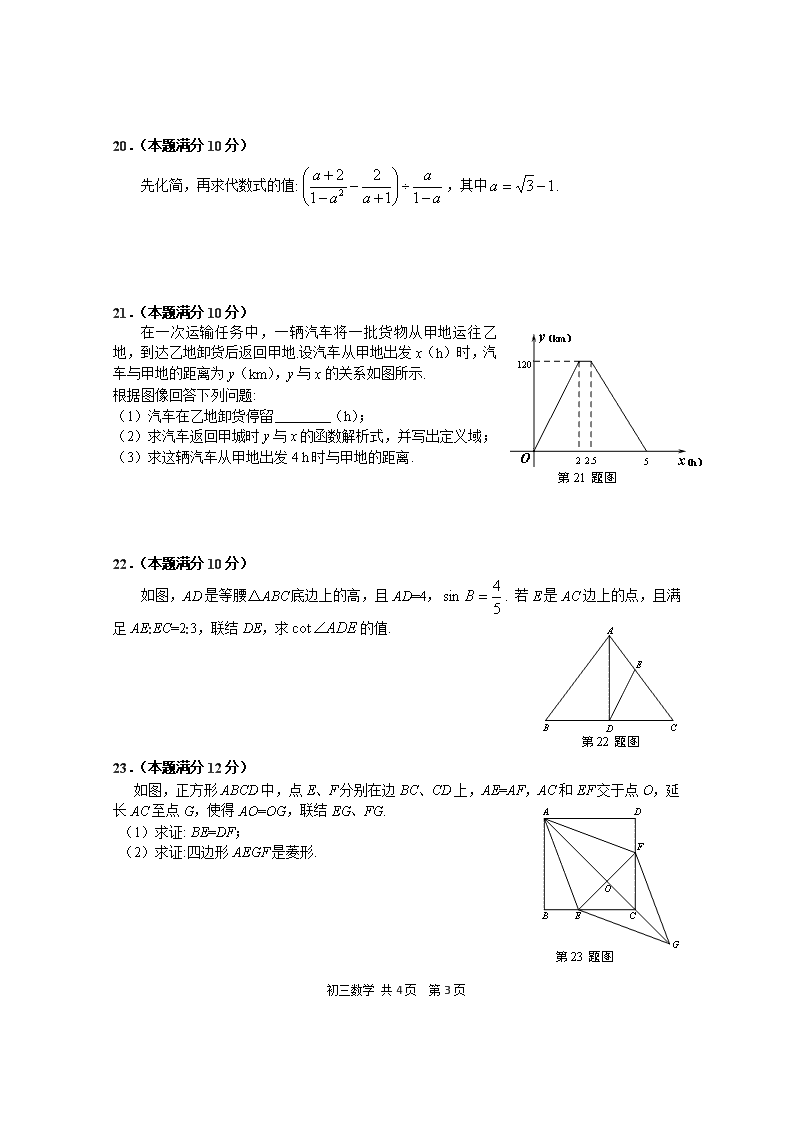
2015年初三数学教学质量检测试卷 (考试时间100分钟,满分150分) 2015.4 考生注意: 1.本试卷含三个大题,共25题.答题时,考生务必按答题要求在答题纸规定的位置上作答,在草稿纸、本试卷上答题一律无效. 2.除第一、二大题外,其余各题如无特别说明,都必须在答题纸的相应位置上写出证明或计 算的主要步骤. 一、单项选择题:(本大题共6题,每题4分,满分24分) 1.将抛物线向右平移3个单位得到的抛物线表达式是( ) A. ; B. ; C. ; D. . 2.下列各式中,与是同类二次根式的是( ) A. ; B. ; C. ; D. . 3. 一组数据: 5,7,4,9,7的中位数和众数分别是( ) A. 4,7 ; B. 7,7 ; C. 4,4 ; D. 4,5 . 4. 用换元法解方程:时,如果设,那么原方程可化为( ) 第6题图 A. ; B. ; C. ; D. . 5. 在下列图形中,①等边三角形,②正方形,③正五边形,④正六边形. 其中既是轴对称图形又是中心对称的图形有( ) A. 1个; B. 2个; C. 3个; D. 4个. 6. 如图,在四边形ABCD中,∠ABC=90°,对角线AC、BD交于点O,AO=CO,∠AOD =∠ADO,E是DC边的中点.下列结论中,错误的是( ) A. ; B. ; C.;; D. . 二、填空题:(本大题共12题,每题4分,满分48分) 7. 计算: = ▲ . 初三数学 共4页 第9页 8. 计算:= ▲ . 9. 方程的解是 ▲ . 第12题图 10.若关于x的二次方程有两个相等的实数根,则实数a = ▲ . 11.从数字1,2,3,4中,任意取两个数字组成一个两位数,这个数是素数的概 率是 ▲ . 12. 2015年1月份,某区体委组织 “迎新春长跑活动”,现将报名的男选手分 成: 青年组、中年组、老年组.各组人数所占比例如图所示,已知青年 组120人,则中年组的人数是 ▲ . 第15题图 13.已知,如果,,那么实数k = ▲ . 14.已知⊙和⊙的半径分别是5和3,若=2,则两圆的位置关系 是 ▲ . 15.已知在离地面30米的高楼窗台A处测得地面花坛中心标志物C的俯角为 60°,那么这一标志物C离此栋楼房的地面距离BC为 ▲ 米. 16.已知线段AB=10,P是线段AB的黄金分割点(AP﹥PB),则AP= ▲ . 17.请阅读下列内容: 第17题图 我们在平面直角坐标系中画出抛物线和双曲线,如图 所示,利用两图像的交点个数和位置来确定方程有一个正 实数根,这种方法称为利用函数图像判断方程根的情况.请用图像法判 断方程的根的情况 ▲ (填写根的个数及正负). 第18题图 18.如图,△ABC≌△DEF(点A、B分别与点D、E对应),AB=AC=5, 且juxingABCD�����������������������������������������������������������������������������������������������������������������BC=6,△ABC固定不动,△DEF运动,并满足点E在BC边从B 向C移动(点E不与B、C重合),DE始终经过点A,EF与AC边交于点M,当△AEM是等腰三角形时,BE= ▲ . 三、解答题:(本大题共7题,满分78分) 19.(本题满分10分) 解不等式组,并将解集在数轴上表示出来 . 初三数学 共4页 第9页 20.(本题满分10分) 先化简,再求代数式的值:,其中. 21.(本题满分10分) 第21题图 在一次运输任务中,一辆汽车将一批货物从甲地运往乙地,到达乙地卸货后返回甲地.设汽车从甲地出发x(h)时,汽车与甲地的距离为y(km),y与x的关系如图所示. 根据图像回答下列问题: (1)汽车在乙地卸货停留 (h); (2)求汽车返回甲城时y与x的函数解析式,并写出定义域; (3)求这辆汽车从甲地出发4 h时与甲地的距离. 22.(本题满分10分) 第22题图 如图,AD是等腰△ABC底边上的高,且AD=4,. 若E是AC边上的点,且满足AE:EC=2:3,联结DE,求的值. 23.(本题满分12分) 第23题图 如图,正方形ABCD中,点E、F分别在边BC、CD上,AE=AF,AC和EF交于点O,延长AC至点G,使得AO=OG,联结EG、FG. (1)求证: BE=DF; (2)求证:四边形AEGF是菱形. 初三数学 共4页 第9页 24.(本题满分12分) 如图,已知抛物线的顶点A在第四象限,过点A作AB⊥y轴于点B,C是线段AB上一点(不与A、B重合),过点C作CD⊥x轴于点D,并交抛物线于点P. (1)若点C的横坐标为1,且是线段AB的中点,求点P的坐标; (2)若直线AP交y轴负半轴于点E,且AC=CP,求四边形OEPD的面积S关于t的函数解析式,并写出定义域; (3)在(2)的条件下,当△ADE的面积等于2S时 ,求t的值. 第24题图 25.(本题满分14分) 如图,已知矩形ABCD,AB =12 cm,AD =10 cm,⊙O与AD、AB、BC三边都相切,与DC交于点E、F。已知点P、Q、R分别从D、A、B三点同时出发,沿矩形ABCD的边逆时针方向匀速运动,点P、Q、R的运动速度分别是1 cm/s、x cm/s、1.5 cm/s,当点Q到达点B时停止运动,P、R两点同时停止运动.设运动时间为t(单位:s). (1)求证: DE=CF; (2)设x = 3,当△PAQ与△QBR相似时,求出t的值; 第25题图 (3)设△PAQ关于直线PQ对称的图形是△PA'Q,当t和x分别为何值时,点A'与圆心O恰好重合,求出符合条件的t、x的值. 初三数学 共4页 第9页 2015年初三数学教学质量检测试卷参考答案 一、单项选择题:(本大题共6题,每题4分,满分24分) 1. A;2. D;3. B;4. A;5. B;6. D. 二、填空题:(本大题共12题,每题4分,满分48分) 7. ; 8. ; 9. -1; 10. 6或-2; 11. ; 12. 40; 13. ±3; 14. 内切; 15. ;16. ; 17. 2正根,1负根; 18. 1或. 二、填空题:(本大题共12题,每题4分,满分48分) 19.(本题满分(10分) 解: (3分) (2分) 化简得 (3分) ∴不等式组的解集是.(2分) 20.(本题满分10分) 解:原式=(2分) =(2分) =(2分) =(2分) ==(2分) 第21题图 21.(本题满分10分) 解:(1)0.5;(2分) 初三数学 共4页 第9页 (2)设(1分) 把(2.5,120)和(5,0)分别代入 得, 解得(3分) ∴解析式为.(1分) (3)当 x = 4时, (2分) ∴这辆汽车从甲地出发4 h时与甲地的距离48 km. (1分) 22.(本题满分10分) 解: 作EF⊥AD于点F. (1分) 第22题图 ∵AD⊥BC ∴∠ADB=90° 在Rt△ABD中,AD=4, ∴AB=5 ∴ ∵等腰△ABC ∴AB=AC ∴AC=5 ∵AD⊥BC ∴DB=DC ∴DC=3 (4分) ∵EF⊥AD AD⊥BC ∴EF//BC ∴ ∵ AC=5 DC=3 ∴EF= AF= DF=(4分) ∴在Rt△EFD中,.(1分) 23.(本题满分12分) 证:(1)∵正方形ABCD ∴AB=AD ∠B=∠D=90° 第23题图 在Rt△ABD和Rt△ACD中 初三数学 共4页 第9页 ∴△ABE≌△ADF ∴BE=DF. (5分) (2)∵正方形ABCD ∴BC=CD ∵ BE=DF ∴CE=CF ∴△ECF是等腰三角形 ∵正方形ABCD ∴AC平分∠BCD ∴AC⊥EF 且EO=OF ∵AO=OG ∴四边形AEGF是平行四边形(5分) ∵AC⊥EF ∴四边形AEGF是菱形. (2分) 24.(本题满分12分) 第24题图 解:(1) ∴A(t,-2)(2分) ∵点C的横坐标为1,且是线段AB的中点 ∴t =2 (1分) ∴ ∴P(1,-1).(1分) (2)据题意,设C(x,-2)(0< x < t),P(x,) AC= t-x,PC= (1分) ∵AC=PC ∴t-x = ∵x < t ∴ t - x=1 即x = t - 1 ∴AC=PC=1 (2分) ∵DC//y轴 ∴ ∴EB= t ∴OE=2-t ∴(1< t <2). (2分) (3) (1分) ∵ ∴ 初三数学 共4页 第9页 解得,(不合题意) ∴ .(2分) 25.(本题满分14分) (1)证:作OH⊥DC于点H,设⊙O与BC边切于点G,联结OG. (1分) 第25题图(1) ∴∠OHC=90° ∵⊙O与BC边切于点G ∴OG=6,OG⊥BC ∴∠OGC=90° ∵矩形ABCD ∴∠C=90° ∴四边形OGCH是矩形 ∴CH=OG ∵OG=6 ∴CH=6 (1分) ∵矩形ABCD ∴AB=CD ∵AB=12 ∴CD=12 ∴DH=CD﹣CH=6 ∴DH= CH ∴O是圆心且OH⊥DC ∴EH=FH (2分) ∴DE=CF. (1分) (2)据题意,设DP=t,PA=10-t,AQ=3t,QB=12-3t,BR=1.5t(0 < t < 4). (1分) ∵矩形ABCD ∴∠A=∠B=90° 若△PAQ与△QBR相似,则有 ① (2分) ② 或(舍)(2分) (3)设⊙O与AD、AB都相切点M、N,联结OM、ON、OA. 第25题图(2) ∴OM⊥AD ON⊥AB 且OM=ON=6 又∵矩形ABCD ∴∠A=90° ∴四边形OMAN是矩形 又∵ OM =ON ∴四边形OMAN是正方形 (1分) ∴MN垂直平分OA ∵△PAQ与△PA'Q关于直线PQ对称 ∴PQ垂直平分OA ∴MN与PQ重合 (1分) ∴ MA = PA = 10-t = 6 ∴ t = 4 (1分) ∴AN = AQ = x t = 6 ∴x = (1分) 初三数学 共4页 第9页 ∴当t = 4 和x =时点A'与圆心O恰好重合. 初三数学 共4页 第9页查看更多