- 2021-05-28 发布 |
- 37.5 KB |
- 22页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
黑龙江省哈尔滨市第九中学2020届高三第三次模拟考试数学(文)试题 Word版含解析
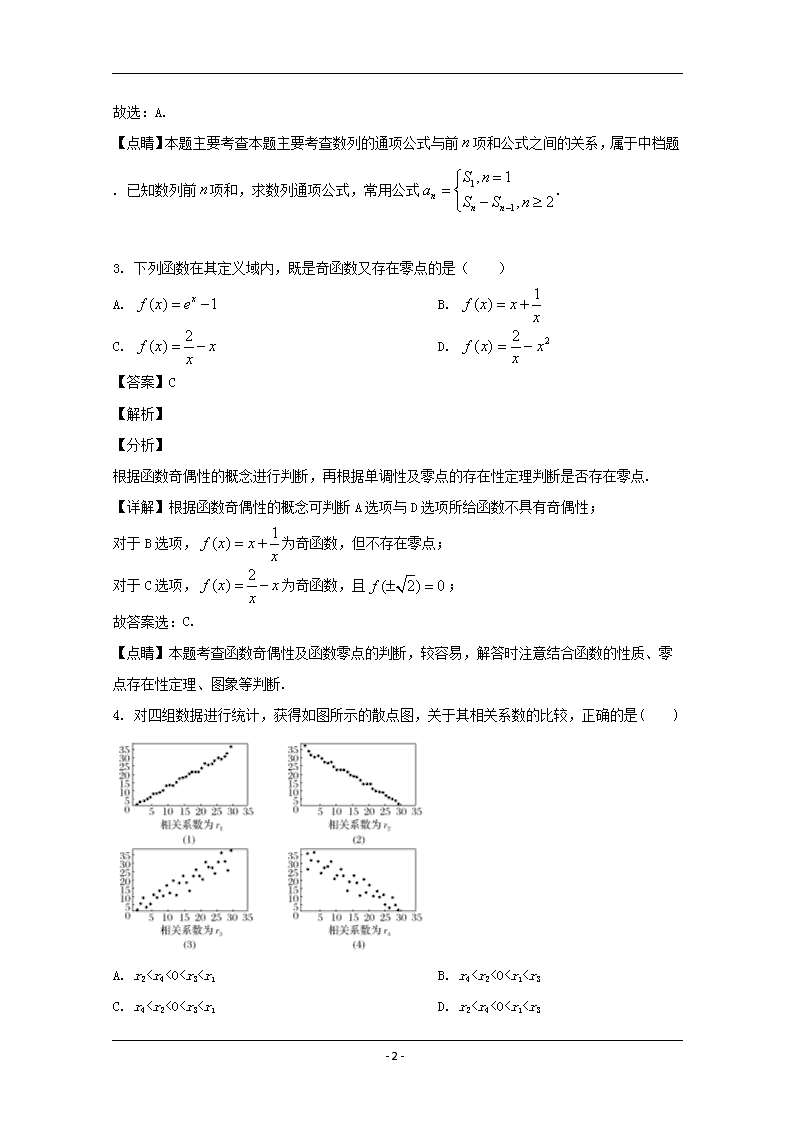
- 1 - 哈尔滨市第九中学 2020 届高三第三次模拟考试 数学试题(文科) 一、选择题 1. 已知集合 A={-1, 1 2 },B={x|mx-1=0},若 A∩B=B,则所有实数 m 组成的集合是 ( ) A. {-1,2} B. {- 1 2 ,0,1} C. {-1,0,2} D. {-1,0, 1 2 } 【答案】C 【解析】 (1) B ,则 0m (2) 1B m ,则 1 1 11 2m m 或 ,解得 1 2m 或 综上, m 1,0,2 选 C 点睛:(1)认清元素的属性,解决集合问题时,认清集合中元素的属性(是点集、数集或其他 情形)和化简集合是正确求解的两个先决条件. (2)注意元素的互异性.在解决含参数的集合问题时,要注意检验集合中元素的互异性,否则 很可能会因为不满足“互异性”而导致解题错误. (3)防范空集.在解决有关 ,A B A B 等集合问题时,往往忽略空集的情况,一定先考 虑是否成立,以防漏解. 2. 设数列{ na }的前 n 项和 ns = 2n ,则 8a 的值为 A. 15 B. 16 C. 49 D. 64 【答案】A 【解析】 【分析】 利用 8 8 7a S S 求解即可. 【详解】因为数列{ }的前 n 项和 ns = 2n , 所以 8 78 64 49 15a S S , - 2 - 故选:A. 【点睛】本题主要考查本题主要考查数列的通项公式与前 n 项和公式之间的关系,属于中档题. 已知数列前 n 项和,求数列通项公式,常用公式 1 1 , 1 , 2n n n S na S S n . 3. 下列函数在其定义域内,既是奇函数又存在零点的是( ) A. ( ) 1xf x e B. 1( )f x x x C. 2( )f x xx D. 22( )f x xx 【答案】C 【解析】 【分析】 根据函数奇偶性的概念进行判断,再根据单调性及零点的存在性定理判断是否存在零点. 【详解】根据函数奇偶性的概念可判断 A 选项与 D 选项所给函数不具有奇偶性; 对于 B 选项, 1( )f x x x 为奇函数,但不存在零点; 对于 C 选项, 2( )f x xx 为奇函数,且 ( 2) 0f ; 故答案选:C. 【点睛】本题考查函数奇偶性及函数零点的判断,较容易,解答时注意结合函数的性质、零 点存在性定理、图象等判断. 4. 对四组数据进行统计,获得如图所示的散点图,关于其相关系数的比较,正确的是( ) A. r2查看更多
相关文章
- 当前文档收益归属上传用户
- 下载本文档