高二数学人教a必修5练习:3-2一元二次不等式及其解法(一)word版含解析
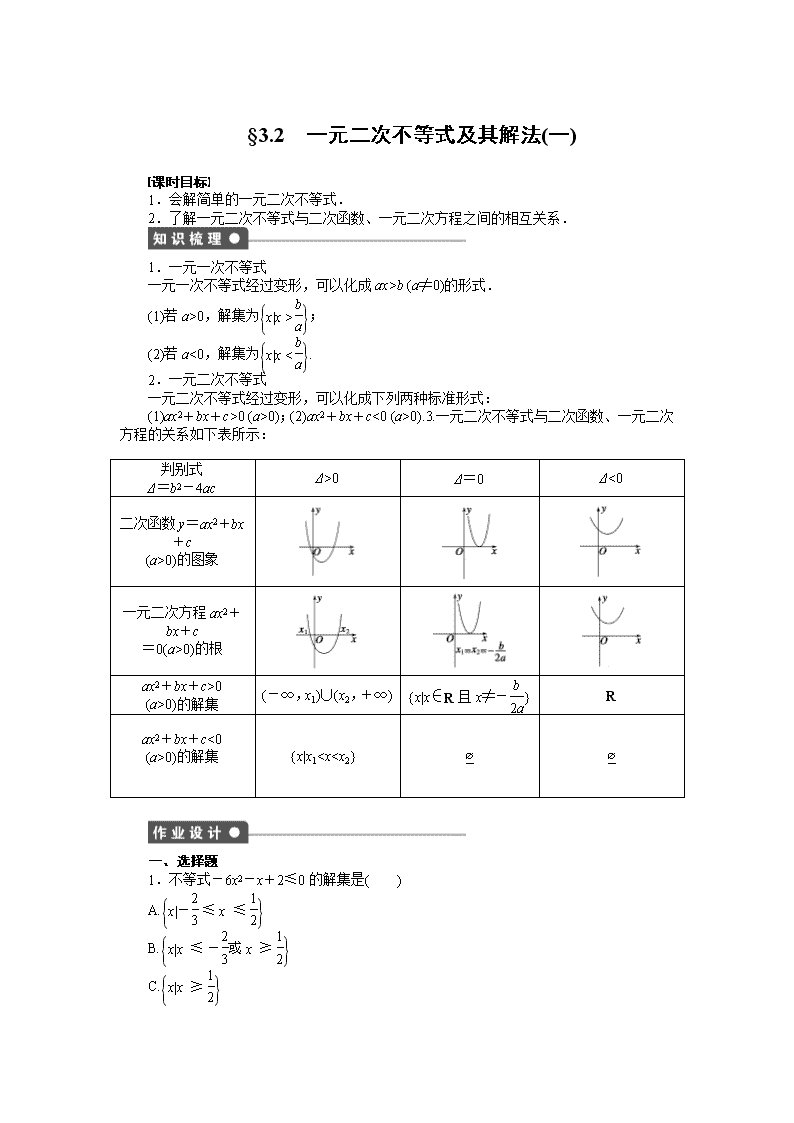
§3.2 一元二次不等式及其解法(一)
课时目标
1.会解简单的一元二次不等式.
2.了解一元二次不等式与二次函数、一元二次方程之间的相互关系.
1.一元一次不等式
一元一次不等式经过变形,可以化成 ax>b (a≠0)的形式.
(1)若 a>0,解集为 x|x>b
a ;
(2)若 a<0,解集为 x|x
0 (a>0);(2)ax2+bx+c<0 (a>0).3.一元二次不等式与二次函数、一元二次
方程的关系如下表所示:
判别式
Δ=b2-4ac Δ>0 Δ=0 Δ<0
二次函数 y=ax2+bx
+c
(a>0)的图象
一元二次方程ax2+bx
+c
=0(a>0)的根
ax2+bx+c>0
(a>0)的解集
(-∞,x1)∪(x2,+
∞) {x|x∈R 且 x≠- b
2a} R
ax2+bx+c<0
(a>0)的解集 {x|x12} B.{x|x≤-1 或 x≥2}
C.{x|-10,
x2+6x≥0,
∴x≤-6 或 x>2.
4.在 R 上定义运算⊙:a⊙b=ab+2a+b,则满足 x⊙(x-2)<0 的实数 x 的取值范围为
( )
A.(0,2) B.(-2,1)
C.(-∞,-2)∪(1,+∞) D.(-1,2)
答案 B
解析 ∵x⊙(x-2)=x(x-2)+2x+x-2<0,
∴x2+x-2<0.∴-20.
当 m=2 时,4>0,x∈R;
当 m<2 时,Δ=(4-2m)2-16(2-m)<0,
解得-2f(1)的解是( )
A.(-3,1)∪(3,+∞) B.(-3,1)∪(2,+∞)
C.(-1,1)∪(3,+∞) D.(-∞,-3)∪(1,3)
答案 A
解析 f(1)=12-4×1+6=3,
当 x≥0 时,x2-4x+6>3,解得 x>3 或 0≤x<1;
当 x<0 时,x+6>3,解得-3f(1)的解是(-3,1)∪(3,+∞).
二、填空题
7.二次函数 y=ax2+bx+c 的部分对应点如下表:
X -3 -2 -1 0 1 2 3 4
y 6 0 -4 -6 -6 -4 0 6
则不等式 ax2+bx+c>0 的解集是______________.
答案 {x|x<-2 或 x>3}
8.不等式-10,
∴-3≤x<-2 或 00 的解集是________________.
答案 {x|x<1- 5
2
或 x>1+ 5
2
}
解析 ∵x2-x+1= x-1
2 2+3
4>0,
∴(x2-x-1)(x2-x+1)>0 可转化为
解不等式 x2-x-1>0,由求根公式知,
x1=1- 5
2
,x2=1+ 5
2 .
∴x2-x-1>0 的解集是
x|x<1- 5
2
或 x>1+ 5
2 .
∴原不等式的解集为 x|x<1- 5
2
或 x>1+ 5
2 .
三、解答题
11.若不等式 ax2+bx+c≥0 的解集为 x|-1
3
≤x≤2 ,求关于 x 的不等式 cx2-bx+a<0
的解集.
解 由 ax2+bx+c≥0 的解集为 x|-1
3
≤x≤2 ,
知 a<0,且关于 x 的方程 ax2+bx+c=0 的两个根分别为-1
3
,2,
∴
-1
3
+2=-b
a
-1
3
×2=c
a
,∴b=-5
3a,c=-2
3a.
所以不等式 cx2-bx+a<0 可变形为
-2
3a x2- -5
3a x+a<0,
即 2ax2-5ax-3a>0.
又因为 a<0,所以 2x2-5x-3<0,
所以所求不等式的解集为 x|-1
20.
解 将不等式 x2-(a+a2)x+a3>0 变形为
(x-a)(x-a2)>0.
∵a2-a=a(a-1).
∴当 a<0 或 a>1 时,aa2}.
当 0a}.
当 a=0 或 1 时,解集为{x|x∈R 且 x≠a}.
综上知,当 a<0 或 a>1 时,不等式的解集为{x|xa2};
当 0a};
当 a=0 或 1 时,不等式的解集为{x|x∈R 且 x≠a}.
【能力提升】
13.已知 a1>a2>a3>0,则使得(1-aix)2<1 (i=1,2,3)都成立的 x 的取值范围是( )
A. 0, 1
a1 B. 0, 2
a1 C. 0, 1
a3 D. 0, 2
a3
答案 B
解析 由(1-aix)2<1,
得 1-2aix+(aix)2<1,
即 ai·x(aix-2)<0.
又 a1>a2>a3>0.
∴0 2
a2
> 2
a1
>0
∴00 时,x≥2
a
或 x≤-1;
当-20 时,解集为 x|x≥2
a
或 x≤-1 ;
当 a=0 时,解集为{x|x≤-1};
当-2
查看更多