高中数学人教a版必修二 第一章 空间几何体 学业分层测评6 word版含答案

高中数学人教a版必修二 第一章 空间几何体 学业分层测评6 word版含答案

学业分层测评(六) (建议用时：45 分钟) [达标必做] 一、选择题 1．设正方体的表面积为 24，那么其外接球的体积是( ) A.4 3π B.8π 3 C．4 3π D．32 3π 【解析】 设正方体边长为 a，由题意可知，6a2＝24，∴a＝2. 设正方体外接球的半径为 R，则 3a＝2R，∴R＝ 3，∴V 球＝4 3πR3＝4 3π. 【答案】 C 2．两个球的体积之比为 8∶27，那么这两个球的表面积之比为 ( ) A．2∶3 B．4∶9 C. 2∶ 3 D. 8∶ 27 【解析】 4 3πr3 ∶ 4 3πR3 ＝r3∶R3＝8∶27， ∴r∶R＝2∶3，∴S1∶S2＝r2∶R2＝4∶9. 【答案】 B 3．把一个铁制的底面半径为 r，高为 h 的实心圆锥熔化后铸成一 个铁球，则这个铁球的半径为( ) A.r h 2 B.r2h 4 C. 3 r2h 4 D.r2h 2 【解析】 ∵1 3πr2h＝4 3πR3，∴R＝3 r2h 4 . 【答案】 C 4．一平面截一球得到直径是 6 cm 的圆面，球心到这个平面的距 离是 4 cm，则该球的体积是( ) 【导学号：09960032】 A.100π 3 cm3 B.208π 3 cm3 C.500π 3 cm3 D.416 13π 3 cm3 【解析】 根据球的截面性质，有 R＝ r2＋d2＝ 32＋42＝5， ∴V 球＝4 3πR3＝500 3 π(cm3)． 【答案】 C 5．等边圆柱(轴截面是正方形)、球、正方体的体积相等，它们的 表面积的大小关系是( ) A．S 球1，故选 A. 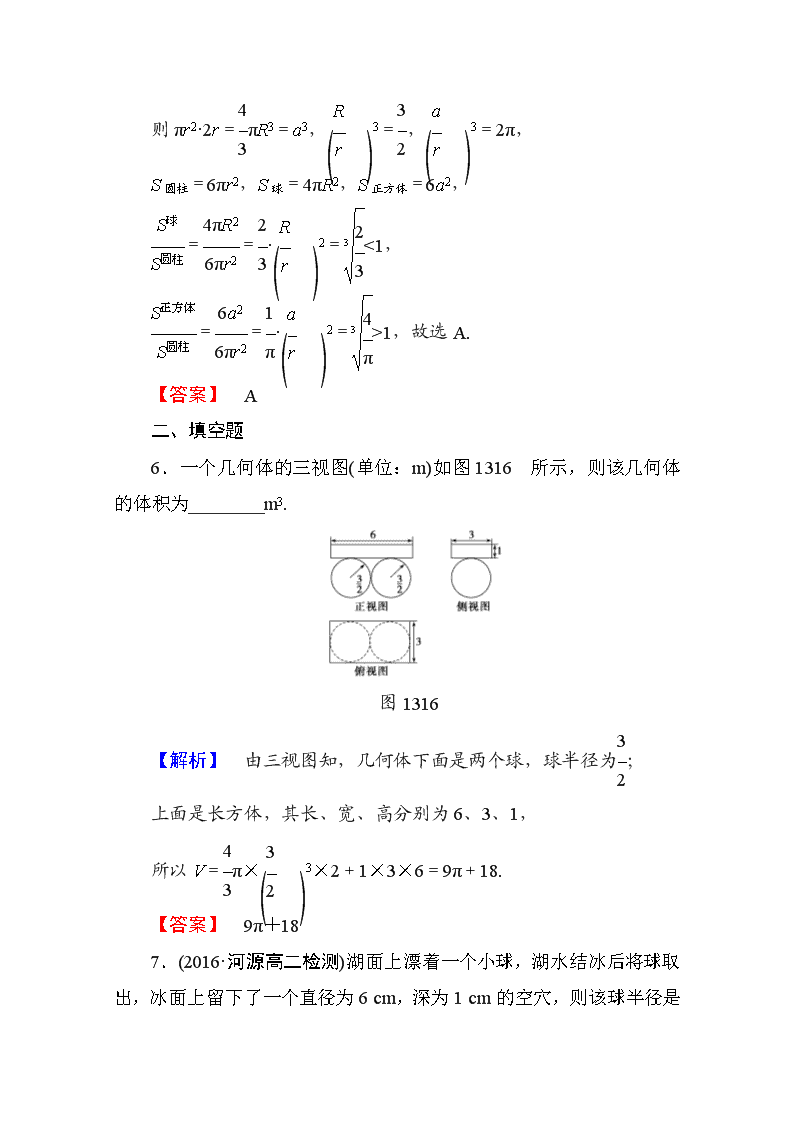【答案】 A 二、填空题 6．一个几何体的三视图(单位：m)如图 1316 所示，则该几何体 的体积为________m3. 图 1316 【解析】 由三视图知，几何体下面是两个球，球半径为3 2 ； 上面是长方体，其长、宽、高分别为 6、3、1， 所以 V＝4 3π× 3 2 3×2＋1×3×6＝9π＋18. 【答案】 9π＋18 7．(2016·河源高二检测)湖面上漂着一个小球，湖水结冰后将球取 出，冰面上留下了一个直径为 6 cm，深为 1 cm 的空穴，则该球半径是 ________cm，表面积是________cm2. 【导学号：09960033】 【解析】 设球心为 O，OC 是与冰面垂直的一条球半径，冰面截 球得到的小圆圆心为 D，AB 为小圆 D 的一条直径，设球的半径为 R， 则 OD＝R－1， 则(R－1)2＋32＝R2， 解得 R＝5 cm， 所以该球表面积为 S＝4πR2＝4π×52＝100π(cm2)． 【答案】 5 100π 三、解答题 8．如图 1317，一个圆柱形的玻璃瓶的内半径为 3 cm，瓶里所装 的水深为 8 cm，将一个钢球完全浸入水中，瓶中水的高度上升到 8.5 cm，求钢球的半径． 图 1317 【解】 设球的半径为 R，由题意可得 4 3πR3＝π×32×0.5， 解得 R＝1.5(cm)，所以所求球的半径为 1.5 cm. 9．(2016·大同高二检测)如图 1318 所示(单位：cm)四边形 ABCD 是直角梯形，求图中阴影部分绕 AB 旋转一周所成几何体的表面积和体 积． 图 1318 【解】 1 2S 球＝1 2 ×4π×22＝8π(cm2)， S 圆台侧＝π(2＋5) 5－22＋42＝35π(cm2)， S 圆台下底＝π×52＝25π(cm2)， 即该几何体的表面积为 8π＋35π＋25π＝68π(cm2)． 又 V 圆台＝π 3 ×(22＋2×5＋52)×4＝52π(cm3)， V 半球＝1 2 ×4π 3 ×23＝16π 3 (cm3)． 所以该几何体的体积为 V 圆台－V 半球＝52π－16π 3 ＝140π 3 (cm3)． [自我挑战] 10．一块石材表示的几何体的三视图如图 1319 所示．将该石材 切削、打磨，加工成球，则能得到的最大球的半径等于( ) 图 1319 A．1 B．2 C．3 D．4 【解析】 由三视图可知该几何体是一个直三棱柱，如图所示．由 题意知，当打磨成的球的大圆恰好与三棱柱底面直角三角形的内切圆 相同时，该球的半径最大，故其半径 r＝1 2 ×(6＋8－10)＝2.因此选 B. 【答案】 B 11．轴截面为正三角形的圆锥内有一个内切球，若圆锥的底面半 径为 2，求球的体积. 【导学号：09960034】 【解】 如图所示，作出轴截面， 因为△ABC 是正三角形， 所以 CD＝1 2AC＝2， 所以 AC＝4，AD＝ 3 2 ×4＝2 3， 因为 Rt△AOE∽Rt△ACD， 所以OE AO ＝CD AC. 设 OE＝R，则 AO＝2 3－R， 所以 R 2 3－R ＝1 2 ，所以 R＝2 3 3 . 所以 V 球＝4 3πR3＝4 3π· 2 3 3 3＝32 3π 27 . 所以球的体积等于32 3π 27 .