- 2021-05-24 发布 |
- 37.5 KB |
- 12页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
北京市石景山中考数学二模试卷及答案
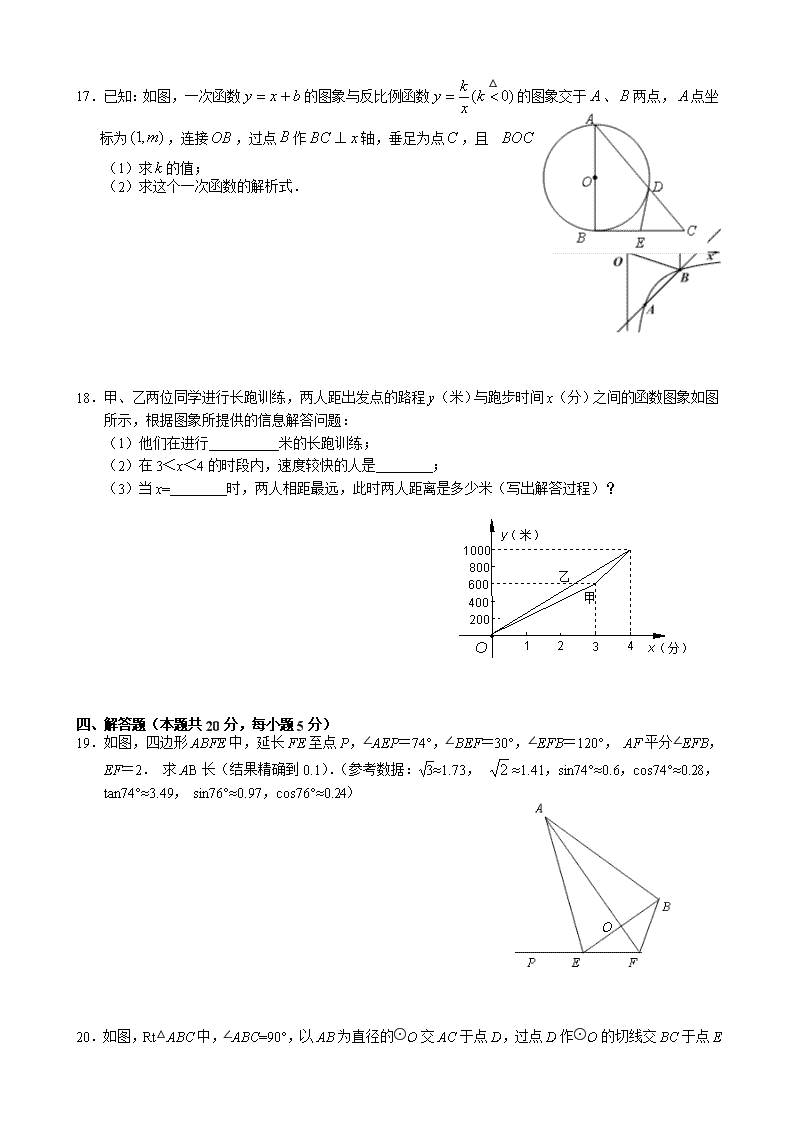
石景山区2013年初三第二次统一练习 数 学 试 卷 一、选择题(本题共32分,每小题4分) 1.3的相反数是( ) A.-3 B.3 C. D. 2.某市政府召开的全市经济形势分析会公布,全市去年地区生产总值(GDP)实现1091亿元,数字1091用科学记数法表示为( ) A. B. C. D. 第 3题图 3.如图,△ABC中,DE是AC的垂直平分线,AE=4cm, △ABD的周长为14cm,则△ABC的周长为( ) A.18 cm B. 22 cm C.24 cm D. 26 cm 4.一射击运动员在一次射击练习中打出的成绩如下表所示:这次成绩的众数、平均数是( ) 成绩(环) 6 7 8 9 10 次数 1 2 2 4 1 A.9, 8 B. 9, 8.2 C. 10, 8 D.10, 8.2 第6题图 5.甲盒装有3个红球和4个黑球,乙盒装有3个红球、4个黑球和5个白球.这些球除了颜色外没有其他区别.搅匀两盒中的球,从盒中分别任意摸出一个球.正确说法是( ) A.从甲盒摸到黑球的概率较大 B.从乙盒摸到黑球的概率较大 C.从甲、乙两盒摸到黑球的概率相等 D.无法比较从甲、乙两盒摸到黑球的概率 6.如图,AB是⊙O的直径,C是⊙O上的一点,若AC=8,AB=10,OD⊥BC于点D,则BD的长为( ) A.6 B.5 C.3 D.1.5 7.若二次函数配方后为,则、的值分别为( ) A.2、6 B.2、8 C.-2、6 D.-2、8 8. 如图是由五个相同的小正方体组成的几何体,则下列说法正确的是( ) 主视图方向 第 8题图 A.左视图面积最大 B.俯视图面积最小 C.左视图面积和主视图面积相等 D.俯视图面积和主视图面积相等 二、填空题(本题共16分,每小题4分) 9.分解因式: = . 10.抛物线的图象和x轴有交点,则k的取值范围是 . 11.已知:平面直角坐标系xoy中,圆心在x轴上的⊙M与y轴交于点(0,4)、点,过作⊙的切线交轴于点,若点M(-3,0),则的值为 . O D . y H A O x M 第 11题图 第 12题图 12.如图,,过上到点的距离分别为1,4,7,10,13,16,…的点作的垂线与相交,得到并标出一组黑色梯形,它们的面积分别为…,观察图中的规律,第4个黑色梯形的面积 ,第n(n为正整数)个黑色梯形的面积 . 三、解答题(本题共30分,每小题5分) 13.计算:. 14.解分式方程:. D C A B F G E 15.如图,四边形ABCD是正方形,G是BC上任意一点(点G与B、C不重合),AE^DG于E,CF∥AE交DG于F.请在图中找出一对全等三角形,并加以证明. 16. 先化简,再求值:,其中x满足. 17.已知:如图,一次函数的图象与反比例函数的图象交于、两点,点坐标为,连接,过点作轴,垂足为点,且△的面积为. (1)求的值; (2)求这个一次函数的解析式. 18.甲、乙两位同学进行长跑训练,两人距出发点的路程y(米)与跑步时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答问题: (1)他们在进行 米的长跑训练; (2)在3<x<4的时段内,速度较快的人是 ; (3)当x= 时,两人相距最远,此时两人距离是多少米(写出解答过程)? 甲 乙 四、解答题(本题共20分,每小题5分) 19.如图,四边形ABFE中,延长FE至点P,∠AEP=74°,∠BEF=30°,∠EFB=120°, AF平分∠EFB,EF=2. 求AB长(结果精确到0.1).(参考数据:≈1.73, ≈1.41,sin74°≈0.6,cos74°≈0.28, O tan74°≈3.49, sin76°≈0.97,cos76°≈0.24) 20.如图,Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,过点D作⊙O的切线交BC于点E . (1)求证:点E为BC中点; (2)若tanEDC=,AD=,求DE的长. 21.为了解某区九年级学生学业考试体育成绩,现从中随机抽取部分学生的体育成绩进行分段(A:40分; B:39-35分; C:34-30分; D:29-20分; E:19-0分)统计如下: 学业考试体育成绩(分数段)统计表 学业考试体育成绩(分数段)统计图 0 分数段 人数(人) 频率 A 48 0.2 B a 0.25 C 84 b D 36 0.15 E 12 0.05 根据上面提供的信息,回答下列问题: (1)在统计表中,的值为_____,的值为______,并将统计图补充完整; (2)甲同学说:“我的体育成绩是此次抽样调查所得数据的中位数. ”请问:甲同学的体育成绩应在什么分数段内?______(填相应分数段的字母) (3)如果把成绩在30分以上(含30分)定为优秀,那么该区今年2400名九年级学生中体育成绩为优秀的学生人数有多少名? 22.如图,在矩形ABCD中,AB=3,BC=4,点M、N、分别在BC、AB上,将矩形ABCD沿MN折叠,设点B的对应点是点E. (1)若点E在AD边上,BM=,求AE的长; (2)若点E在对角线AC上,请直接写出AE 的取值范围: . 五、解答题(本题共22分,第23题7分,第24题7分,第25题8分) 23.如图,抛物线过点A(-1,0),B(3,0),其对称轴与x轴的交点为C, 反比例函数(x>0,k是常数)的图象经过抛物线的顶点D. (1)求抛物线和反比例函数的解析式. y x O (2)在线段DC上任取一点E,过点E作轴平行线,交y轴于点F、交双曲线于点G,联结DF、DG、FC、GC. ①若△DFG的面积为4,求点G的坐标; ②判断直线FC和DG的位置关系,请说明理由; ③当DF=GC时,求直线DG的函数解析式. 24.如图,四边形、是两个边长分别为5和1且中心重合的正方形.其中,正方形可以绕中心旋转,正方形静止不动. (1)如图1,当四点共线时,四边形的面积为 __; (2)如图2,当三点共线时,请直接写出= _________; (3)在正方形绕中心旋转的过程中,直线与直线的位置关系是______________,请借助图3证明你的猜想. 图1 图2 图3 25.(1)如图1,把抛物线平移后得到抛物线,抛物线经过点和原点,它的顶点为,它的对称轴与抛物线交于点,则抛物线的解析式为____________;图中阴影部分的面积为_____. (2)若点为抛物线上的动点,我们把时的△称为抛物线的内接直角三角形.过点做轴的垂线,抛物线的内接直角三角形的两条直角边所在直线、与直线分别交于、两点,以为直径的⊙与轴交于、两点,如图2.请问:当点在抛物线上运动时,线段的长度是否会发生变化?请写出并证明你的判断. 图2 图1 石景山区2013初三第二次统一练习 数学参考答案 阅卷须知: 1.一律用红钢笔或红圆珠笔批阅. 2.为了阅卷方便,解答题中的推导步骤写得较为详细,考生只要写明主要过程即可.若考生的解法与本解法不同,正确者可参照评分参考给分,解答右端所注分数,表示考生正确做到这一步应得的累加分数. 一、选择题(本题共8道小题,每小题4分,共32分) 题 号 1 2 3 4 5 6 7 8 答 案 A B B B A C C D 二、填空题(本题共4道小题,每小题4分,共16分) 9.; 10.且; 11.; 12.;. 三、解答题(本题共6道小题,每小题5分,共30分) 13.解:原式= ……………………………………………………4分 = ………………………………………………………5分 14. 解: ………………………………………………………2分 ∴ ……………………………………………………………4分 经检验: 是原方程的增根………………………………………………5分 ∴是原方程的根. 15.证明:略(找出全等三角形1分;证明4分) 16.解:原式 …………………………………………………………2分 由,得 ……………………………………… 3分 由题意, ……………………………………………………… 4分 ∴原式. ………………………………………………………5分 17. 解:(1)设点的坐标为,则有,即: …………1分 ∵△的面积为,∴, …………………2分 ∴=-3. …………………………………………………………3分 (2)∵,∴,当时,, ∴点坐标为,……………………………………………………………4分 把点坐标代入得,这个一次函数的解析式为. …5分 18.解:(1)1000米; ……..……..………..……..…..……………………..1分 (2)甲 ………………..……..……..……..……..…………..2分 (3)设l乙:,过(4,1000),故 ……………………..3分 在0<x3的时段内,设l甲:,过(3,600),故……..4分 当时,. 答:当时,两人相距最远,此时两人距离是150米 ………..……..……..5分 四、解答题(本题共20分,每小题5分) 19. 解:由∠EFB=120°,AF平分∠EFB, ∴∠EFO=60°,∠EOF=90°………………………………………………………..1分 ∴FE=FB ………………………………………………………..2分 Rt△EOF中, ∴OE……………………………………………………………..3分 Rt△EOA中, ∴AE ……………………………………..4分 在△和△中 ∴△≌△ ∴AB=AE ……………………………………………..5分 20.解: (1)连结OD, ∵AB为直径,∴∠ADB=90°,又∠ABC=90°, ∴BC是⊙O切线 ………………………………………………..1分 ∵DE是⊙O切线 ∴BE=DE, ∴∠EBD=∠EDB, ∵∠ADB=90°,∴∠EBD+∠C=90°,∠EDB+∠CDE=90°,∴∠C=∠EDC, ∴DE=CE, ∴BE=CE. ………………………………………………..2分 (2) ∵∠ABC=90°,∠ADB=90°, ∴∠C=∠ABD=∠EDC, Rt△ABD中,DB=, …………………………………..3分 Rt△BDC中,BC=,………………………………..4分 又点E为BC中点,∴=3 .……………………………………..5分 21.60 学业考试体育成绩(分数段)统计图 0 解:(1) 60 , 0.35 ,补充后如右图:………………………… 3分 (2) C ; ……………4分 (3)0.8×2400=1920(名) 答:该区九年级考生中体育成绩 为优秀的学生人数有1920名. …………………………5分 22.解:(1)由题意,△BMN沿MN折叠得到△EMN ∴△BMN≌△EMN ∴EM=BM=. 过点M作MH⊥AD交AD于点H,则四边形ABMH为矩形 MH=AB=3, AH=BM=. Rt△EHM中, EH= ∴AE. ……………………………… 3分 (2) 1≤AE≤3. ……………………………… 5分 五、解答题(本题共22分,第23题7分,第24题7分,第25题8分) 23.解: (1)抛物线过点A(-1,0),B(3,0) 解得: ∴抛物线的解析式为 顶点 函数,是常数)图象经过, .…………………………………………………………………… 2分 (2)①设G点的坐标为, 据题意,可得E点的坐标为,F点的坐标为, ,,. 由的面积为4,即,得,点G的坐标为. ………………………………………………… 3分 ②直线FC和DG平行.理由如下: 方法1:利用相似三角形的性质. 据题意,点的坐标为,, ,易得,, ,. . ∴△∽△ ………………………………………………… 5分 方法2:利用正切值. 据题意,点的坐标为,, ,易得,, ,. . ③解:方法1: ,当时,有两种情况: 当时,四边形是平行四边形, 由上题得,,,得. 点G的坐标是(2,2). 设直线的函数解析式为,把点的坐标代入, 得解得 直线的函数解析式是.…………………………………… 6分 当FD与CG所在直线不平行时,四边形是等腰梯形, 则,,点G的坐标是(4,1). 设直线的函数解析式为,把点的坐标代入, 得解得 直线的函数解析式是.…………………………………… 7分 综上所述,所求直线的函数解析式是或. 方法2. 在Rt⊿DFE中,, 在Rt⊿GEC中,,, 解方程得:或 当时,点G的坐标是(2,2). 设直线的函数解析式为,把点的坐标代入, 得解得 直线的函数解析式是. 当时,点G的坐标是(4,1). 设直线的函数解析式为,把点的坐标代入, 得解得 直线的函数解析式是. 综上所述,所求直线的函数解析式是或. 注:不同解法酌情给分 24. 解:(1)==6;…………………………1分 (2)=; ……………………2分 (3). ……………………3分 证明:连接,延长 交于点.如图所示:……4分 由正方形的性质可知: , 即: △≌△ ………………………………………5分 即:. ………………………………………7分 25.解:(1)抛物线的解析式为; 图中阴影部分的面积与△的面积相同,. ∴阴影部分的面积为8. …………………………………… 2分 (2)由题意可知,抛物线只存在两个内接直角三角形. 当点在抛物线上运动时线段的长度不会发生变化. 证明: ∵为⊙的直径, ∴, ∵, ∴△∽△ ∴, 连接,,在△和△中, , ∴△∽△ …………………………………… 6分 ∴ ∴, ∴. …………………………………… 8分查看更多