四年级下册数学教案 -4《三角形的三边关系》 ︳青岛版 (7)

四年级下册数学教案 -4《三角形的三边关系》 ︳青岛版 (7)

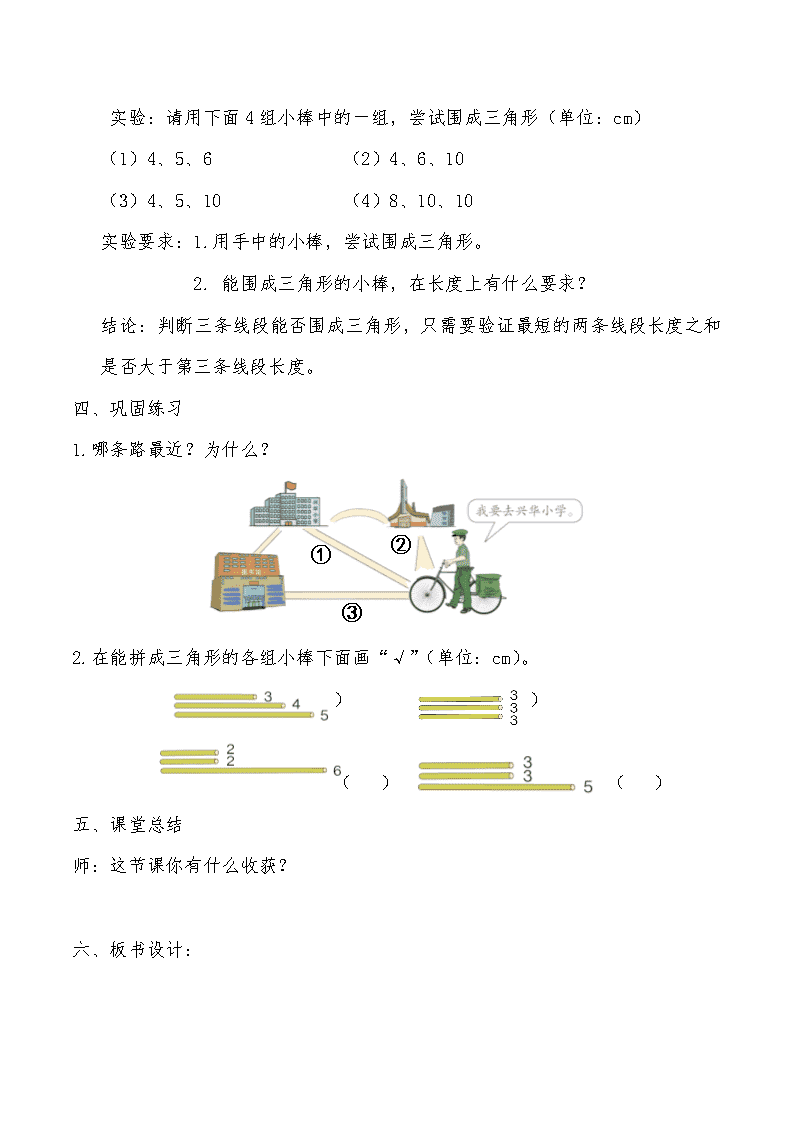
三角形三边的关系 教学目标： 1． 通过观察、操作、实验等活动，探索并发现 “三角形两边之和大于第三 边”这一规律。 2． 经历探究过程，培养学生自主探究、合作交流的能力 3． 在学习的过程中体会数学知识之间的的密切联系，培养合作意识和探索精 神，养成善于观察、勤于思考的良好学习习惯。 教学重点： 理解并掌握三角形三边的关系。 教学难点： 应用三角形三边的关系解决问题。 教学过程： 一、 导入 线段公理 在 A、B 两个点之间，我们连了若干条线，认真观察，哪一条连线最短？它 有什么特点？ 教师总结：两点之间的连线，线段最短。 二、 探究新知 利用课件隐去多余的连线，只剩下下面这幅图。 ① ② ④ ⑤⑤ ② ③ ③ ④ A B 师：根据刚才讨论，我们知道从 A 点到 B 点的连线中，上面两条线段长度的和一 定大于下面的线段，所以 a+b＞c。 2．三角形三边的关系。 （1）师：这两条连线组成我们学过的什么图形？那么我们可以把刚才找最短连 线的问题，转化成研究三角形三条边的长度问题。 师：通过比较两种路线的长度，你发现三角形三边之间有怎样的关系？ （2）揭示规律的必要性。[结合学生发言，板书：三角形两边之和大于第三边。] （3）揭示规律的充分性。 师：还有别的两边之和大于第三边的情况吗？ 同桌讨论，得出结论：a+c＞b ， c +b＞a 。 师：刚才的探究结果，是基于老师屏幕上的三角形得出来的，那其他三角形 是否也有这个结果呢？ 学生验证自己画的三角形三条边是否有这个结论。 师：我们一起验证了多个不同的三角形，都有这个结果，所以三角形两边之和大 于第三边。既然无论选哪两边的和与第三边比较，都得到这个结果，那么你认为 这个结论应该补充一个什么词呢？为什么要加这个词？这个词有什么含义？ [板书修正结论：三角形任意两边之和大于第三边] 三、 实验：探究围成三角形的条件 实验：请用下面 4 组小棒中的一组，尝试围成三角形（单位：cm） C A B （1）4、5、6 （2）4、6、10 （3）4、5、10 （4）8、10、10 实验要求：1.用手中的小棒，尝试围成三角形。 2. 能围成三角形的小棒，在长度上有什么要求？ 结论：判断三条线段能否围成三角形，只需要验证最短的两条线段长度之和 是否大于第三条线段长度。 四、巩固练习 1.哪条路最近？为什么？ 2.在能拼成三角形的各组小棒下面画“√”（单位：cm）。 （ ） （ ） （ ） （ ） 五、课堂总结 师：这节课你有什么收获？ 六、板书设计： √ （ （ （（ ① ② ③ 任意两条线段的和大于第三条线段 C A B 三角形的三边不等关系 两点之间的连线，线段最短 三角形任意两边之和大于第三边 a+b＞c a+c＞b b+c＞a