高中数学2_3_2两个变量的线性相关教案新人教B版必修3

高中数学2_3_2两个变量的线性相关教案新人教B版必修3

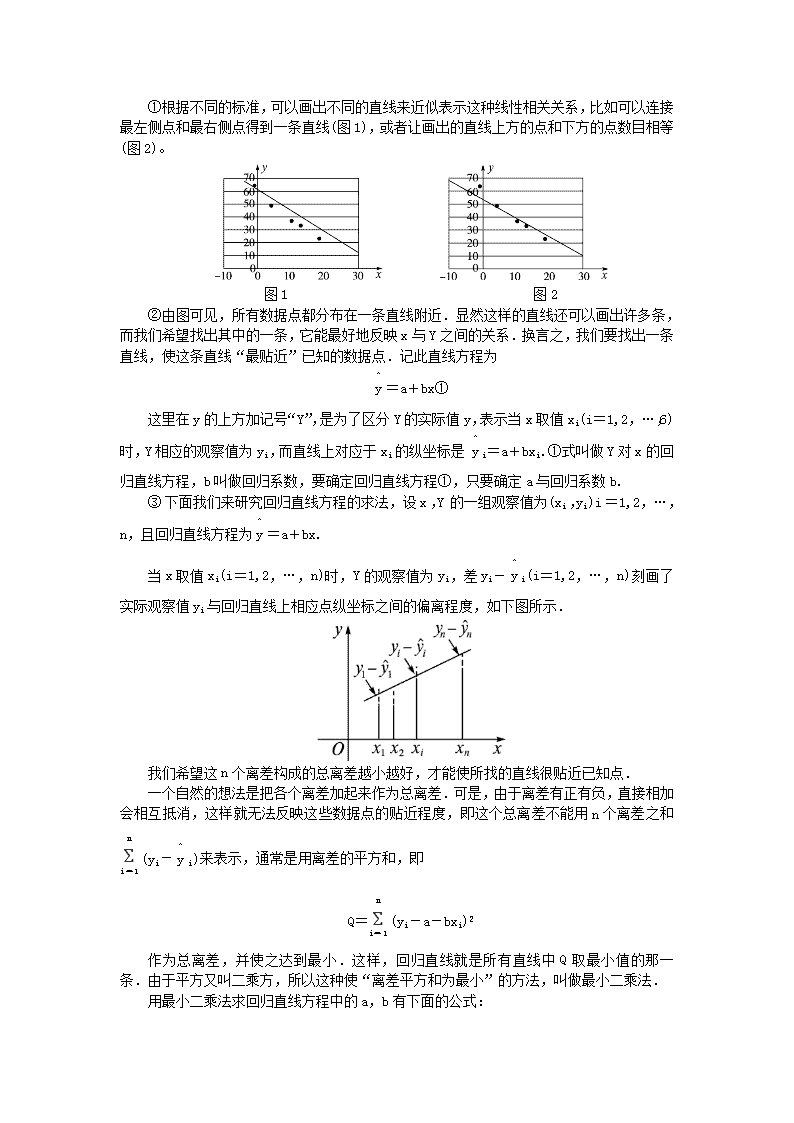
高中数学 2.3.2 两个变量的线性相关教案 新人教 B 版必修 3 整体设计 教学分析 由于用具体的例子来解释线性回归容易理解，所以建议以实际例子引入，让学生用散点 图直观认识两个变量的相关关系，让学生尝试找到最佳的近似直线． 值得注意的是：求回归直线方程，通常是用计算器来完成的，在很多函数型科学计算器 中，可通过直接按键得出线性回归方程的系数，教科书中给出了操作过程，而如果要用一般 的科学计算器进行计算，则要先列出相应的表格． 三维目标 1．经历用不同估算方法描述两个变量线性相关的过程，会建立线性回归方程． 2．能利用回归方程估计变量的值，提高学生解决问题的能力． 3．通过对数据的分析，增强学生的社会实践能力． 重点难点 教学重点：会求线性回归方程，并进行线性回归分析，体会最小二乘法的思想． 教学难点：用最小二乘法求线性回归方程． 课时安排 1 课时 教学过程 导入新课 思路 1.根据一组观测到的数据确定变量 x 与 y 之间是线性相关关系，如果 x 取一个值， 那么怎样估计变量 y 的值呢？教师点出课题． 思路 2.如果散点图中各点在一条直线附近，那么这两个变量具有线性相关关系，那么 怎样求出这条直线方程呢？教师点出课题． 推进新课 新知探究 提出问题 ①变量 x 与 y 的散点图如下图所示，如果近似成线性关系的话，请画出一条直线来近似 地表示这种线性关系． ②同学们也可以自己尝试制定标准来画出近似直线，关键在于这一标准是否合理，是否 能够得到最佳的近似直线(最优拟合直线)． ③怎样确定 a 与 b 呢？ ④写出求回归直线方程的算法． 讨论结果： ①根据不同的标准，可以画出不同的直线来近似表示这种线性相关关系，比如可以连接 最左侧点和最右侧点得到一条直线(图 1)，或者让画出的直线上方的点和下方的点数目相等 (图 2)。 图 1 图 2 ②由图可见，所有数据点都分布在一条直线附近．显然这样的直线还可以画出许多条， 而我们希望找出其中的一条，它能最好地反映 x 与 Y 之间的关系．换言之，我们要找出一条 直线，使这条直线“最贴近”已知的数据点．记此直线方程为 y^＝a＋bx① 这里在 y 的上方加记号“Y”，是为了区分 Y 的实际值 y，表示当 x 取值 xi(i＝1,2，…， 6)时，Y 相应的观察值为 yi，而直线上对应于 xi 的纵坐标是 y^ i＝a＋bxi.①式叫做 Y 对 x 的 回归直线方程，b 叫做回归系数，要确定回归直线方程①，只要确定 a 与回归系数 b. ③下面我们来研究回归直线方程的求法，设 x，Y 的一组观察值为(xi，yi) i＝1,2，…， n，且回归直线方程为y^＝a＋bx. 当 x 取值 xi(i＝1,2，…，n)时，Y 的观察值为 yi，差 yi－y^ i(i＝1,2，…，n)刻画了实 际观察值 yi 与回归直线上相应点纵坐标之间的偏离程度，如下图所示． 我们希望这 n 个离差构成的总离差越小越好，才能使所找的直线很贴近已知点． 一个自然的想法是把各个离差加起来作为总离差．可是，由于离差有正有负，直接相加 会相互抵消，这样就无法反映这些数据点的贴近程度，即这个总离差不能用 n 个离差之和 错误!(yi－y^ i)来表示，通常是用离差的平方和，即 Q＝错误!(yi－a－bxi)2 作为总离差，并使之达到最小．这样，回归直线就是所有直线中 Q 取最小值的那一条．由 于平方又叫二乘方，所以这种使“离差平方和为最小”的方法，叫做最小二乘法． 用最小二乘法求回归直线方程中的 a，b 有下面的公式： b^＝错误!，a^＝ y －b^ x ，其中 a，b 的上方加“y”，表示是由观察值按最小二乘法求 得的估计值，b^也叫回归系数，a^，b^求出后，回归直线方程就建立起来了． ④算法： S1 列表： 序号 x Y x2 xy 1 2 3 … … … … … n ∑ S2 计算a^，b^的值． b^＝错误!，a^＝ y －b^ x ， S3 写出回归直线方程y^＝a^x＋b^. 应用示例 思路 1 例 1 某小卖部 6 天卖出热茶的杯数与当天气温之间是线性相关的．数据如下表： 温度 t/℃ 26 18 13 10 4 －1 杯数 Y 20 24 34 38 50 64 试用最小二乘法求出线性回归方程． 解：从散点图中可以看出，表中的两个变量是线性相关的． 先列表求出 x ＝35 3 ， y ＝115 3 ，其他数据如下表． 序号 x Y x2 xy 1 26 20 676 520 2 18 24 324 432 3 13 34 169 442 4 10 38 100 380 5 4 50 16 200 6 －1 64 1 －64 合计 70 230 1 286 1 910 进而，可以求得b^＝ 1 910－6×35 3 ×115 3 1 286－6×35 3 ×35 3 ≈－1.648，a^＝ y －b^ x ≈57.557. 于是，线性回归方程为y^＝57.557－1.648x. 点评：利用a^＝ y －b^ x 求得a^的值，则有 y ＝b^ x ＋a^，所以求得的线性回归方程y^＝b^x ＋a^必过点( x ， y )． 变式训练 假设关于某设备的使用年限 x 和所支出的维修费用 Y(万元)有如下的统计资料： 使用年限 x 2 3 4 5 6 维修费用 Y 2.2 3.8 5.5 6.5 7.0 若由资料知 Y 对 x 呈线性相关关系．试求回归直线方程． 分析：因为 Y 对 x 呈线性相关关系，所以可以用线性相关的方法解决问题．利用公式：b^＝错误!，a^＝ y －b^ x 来计算回归系数．有时为了方便常制表对应出 xiyi，x2 i，以利于求和． 解：制表： 序号 1 2 3 4 5 合计 x 2 3 4 5 6 20 Y 2.2 3.8 5.5 6.5 7.0 25 xy 4.4 11.4 22.0 32.5 42.0 112.3 x2 4 9 16 25 36 90 x ＝4， y ＝5，错误!2 i＝90，错误!iyi＝112.3 于是有b^＝112.3－5×4×5 90－5×42 ＝12.3 10 ＝1.23，a^＝ y －b^ x ＝5－1.23×4＝0.08. 所以回归直线方程是y^＝1.23x＋0.08. 例 2 在某种产品表面进行腐蚀刻线试验，得到腐蚀深度 Y 与腐蚀时间 x 之间相应的一组 观察值如下表： x/s 5 10 15 20 30 40 50 60 70 90 120 Y/μ m 6 10 10 13 16 17 19 23 25 29 46 (1)画出表中数据的散点图； (2)求 Y 对 x 的回归直线方程；(结果保留到小数点后 3 位数字) (3)试预测腐蚀时间为 100 s 时腐蚀深度是多少． 分析：利用回归直线方程预测腐蚀时间为 100 s 时腐蚀深度． 解：(1)散点图如下图． (2)根据公式②求腐蚀深度 Y 对腐蚀时间 x 的回归直线方程的步骤如下： Ⅰ.先把数据列成表． 序号 x Y x2 xy 1 5 6 25 30 2 10 10 100 100 3 15 10 225 150 4 20 13 400 260 5 30 16 900 480 6 40 17 1 600 680 7 50 19 2 500 950 8 60 23 3 600 1 380 9 70 25 4 900 1 750 10 90 29 8 100 2 610 11 120 46 14 400 5 520 ∑ 510 214 36 750 13 910 Ⅱ.计算a^，b^的值． 由上表分别计算 x，y 的平均数得 x ＝510 11 ， y ＝214 11 .代入公式②得(注意：不必把 x ， y 化为小数，以减小误差) b^＝ 13 910－11×510 11 ×214 11 36 750－11× 510 11 2 ≈0.304 3≈0.304 a^＝214 11 －0.304 3×510 11 ≈5.346. Ⅲ.写出回归直线方程． 腐蚀深度 Y 对腐蚀时间 x 的回归直线方程为 y^＝0.304x＋5.346. 这里的回归系数b^＝0.304，它的意义是：腐蚀时间 x 每增加一个单位(s)，深度 Y 平均 增加 0.304 个单位(μm)． (3)根据上面求得的回归直线方程，当腐蚀时间为 100 s 时，y^＝0.304×100＋5.346＝ 35.86(μm)，即腐蚀深度大约是 35.86 μm. 点评：利用回归直线方程可以对总体进行预测，值得注意的是得出的回归直线方程并不 是函数解析式. 变式训练 高三一班学生每周用于数学学习的时间 x(单位：h)与数学成绩 Y(单位：分)之间有如下数据： x/h 24 15 23 19 16 11 20 16 17 13 Y/分 92 79 97 89 64 47 83 68 71 59 某同学每周用于数学学习的时间为 18 小时，试预测该生数学成绩． 分析：两个有相关关系的变量间的关系可以用线性回归方程来表示，对总体的预测可由回归直线 方程来解决． 解：利用计算器求得b^≈3.53，a^≈13.48，因此可求得回归直线方程为 y^＝3.53x＋13.48， 当 x＝18 时，y^＝3.53×18＋13.48≈77. 故该同学预计可得 77 分左右. 思路 2 例 1 给出施化肥量对水稻产量影响的试验数据： 施化肥量 x 15 20 25 30 35 40 45 水稻产量 y 330 345 365 405 445 450 455 (1)画出上表的散点图； (2)求出回归直线的方程． 解：(1)散点图如下图． (2)计算得b^≈4.75，a^≈257.从而得回归直线方程是y^＝257＋4.75x. 变式训练 一个车间为了规定工时定额，需要确定加工零件所花费的时间．为此进行了 10 次试验，测 得数据如下： 零件 个数 x/个 10 20 30 40 50 60 70 80 90 100 加工 时间 Y/分 62 68 75 81 89 95 102 108 115 122 请判断 Y 与 x 是否具有线性相关关系，如果 Y 与 x 具有线性相关关系，求线性回归方程． 解：在直角坐标系中画出数据的散点图，如下图. 直观判断散点在一条直线附近，故具有线性相关关系．由测得的数据表可知：b^≈0.668，a^＝ y －b^ x ≈54.96. 因此，所求线性回归方程为y^＝b^x＋a^＝54.96＋0.668x. 2 设对变量 x，Y 有如下观察数据： x 151 152 153 154 156 157 158 160 160 162 163 164 Y 40 41 41 41.5 42 42.5 43 44 45 45 46 45.5 使用函数型计算器求 Y 对 x 的回归直线方程．(结果保留到小数点后 3 位数字) 解：按键 MODE 3 1 (进入线性回归计算状态) SHIFT CLR 1 ＝ (将计算器存储器设置成初始状态) 151 ， 40 DT 152 ， 41 DT 153 ， 41 DT 154 ， 41.5 DT 156 ， 42 DT 157 ， 42.5 DT 158 ， 43 DT 160 ， 44 DT 160 ， 45 DT 162 ， 45 DT 163 ， 46 DT 164 ， 45.5 DT 继续按下表按键 按键 显示结果 SHIFT SVAR 1 ＝ －27.75938967 SHITF SVAR 2 ＝ 0.449530516 即 a^≈－27.759，b^≈0.450. 所以 Y 对 x 的回归直线方程为y^＝0.450x－27.759. 点评：利用计算器求回归直线方程非常方便. 变式训练 下表为某地近几年机动车辆数与交通事故数的统计资料. 机动车 辆数 x/ 千台 95 110 112 120 129 135 150 180 交通事 故数 Y/ 千件 6.2 7.5 7.7 8.5 8.7 9.8 10.2 13 (1)请判断机动车辆数与交通事故数之间是否有线性相关关系，如果不具有线性相关关系，请 说明理由； (2)如果具有线性相关关系，求出线性回归方程． 解：(1)在直角坐标系中画出数据的散点图，如下图． 直观判断散点在一条直线附近，故具有线性相关关系． (2)计算得b^≈0.077 4，a^＝－1.024 1， 所以，所求线性回归方程为y^＝－1.024 1＋0.077 4x. 知能训练 1．已知 10 只狗的血球体积及红血球数的测量值如下： 血球 体积 x/mL 45 42 46 48 42 35 58 40 39 50 红血 球数 Y/百 6.53 6.30 9.52 7.50 6.99 5.90 9.49 6.20 6.55 8.72 万 (1)画出上表的散点图； (2)求出回归直线的方程． 2．以下是收集到的新房屋销售价格 y 与房屋大小 x 的数据： 房屋大小 x/m2 80 105 110 115 135 销售价格 Y/万元 18.4 22 21.6 24.8 29.2 (1)画出数据的散点图； (2)用最小二乘法估计求线性回归方程． 参考答案： 1．解：(1)散点图如下图所示． (2) x ＝ 1 10 (45＋42＋46＋48＋42＋35＋58＋40＋39＋50)＝44.50， y ＝ 1 10 (6.53＋6.30＋9.52＋7.50＋6.99＋5.90＋9.49＋6.20＋6.55＋8.72)＝7.37. 设回归直线方程为y^＝a^＋b^x，则b^＝0.175，a^＝ y －b^ x ＝－0.418， 所以所求回归直线的方程为y^＝－0.418＋0.175x. 2．解：(1)散点图如下图． (2)计算得b^≈0.196 2，a^≈1.816 6，所以，线性回归方程为y^＝1.816 6＋0.196 2x. 拓展提升 某调查者从调查中获知某公司近年来科研费用支出x与公司所获得利润Y的统计资料如 下表： 科研费用支出 x 与利润 Y 统计表 单位：万元 年份 科研费用支出 利润 1998 5 31 1999 11 40 2000 4 30 2001 5 34 2002 3 25 2003 2 20 合计 30 180 要求估计利润 Y 对科研费用支出 x 的线性回归模型． 解：设线性回归模型直线方程为y^＝a^＋b^x， 因为 x ＝30 6 ＝5， y ＝180 6 ＝30， 求解a^、b^的估计值：b^＝2，a^＝20. 所以利润 Y 对科研费用支出 x 的线性回归模型直线方程为y^＝20＋2x. 课堂小结 1．求线性回归方程． 2．经历用不同估算方法描述两个变量线性相关的过程．知道最小二乘法的思想，能根 据给出的线性回归方程系数公式建立线性回归方程． 作业 本节练习 B 1、2. 设计感想 本节课在上节课的基础上，利用实例分析了散点图的分布规律，推导出了线性回归直线 的方程的求法，并利用回归直线的方程估计可能的结果，本节课讲得较为详细，实例较多， 便于同学们分析比较．本节课通过选取一些学生特别关心的身边事例，对学生进行思想情操 教育、意志教育，使其养成良好的学习态度． 备课资料 相关关系的强与弱 我们知道，两个变量 x、y 正(负)相关时，它们就有相同(反)的变化趋势，即当 x 由小 变大时，相应的 y 有由小(大)变大(小)的趋势，因此可以用回归直线来描述这种关系．与此 相关的一个问题是：如何描述 x 和 y 之间的这种线性关系的强弱？例如，物理成绩与数学成 绩正相关，但数学成绩能够在多大程度上决定物理成绩？这就是相关强弱的问题，类似的还 有吸烟与健康的负相关强度、父母身高与子女身高的正相关强度、农作物的产量与施肥量的 正相关强度等． 统计中用相关系数 r 来衡量两个变量之间线性关系的强弱．若相应于变量 x 的取值 xi， 变量 y 的观测值为 yi(1≤i≤n)，则两个变量的相关系数的计算公式为 r＝错误!. 不相同的相关性可以从散点图上直观地反映出来．图(1)反映了变量 x、y 之间很强的线 性相关关系，而图(2)中的两个变量的线性相关程度很弱． 对于相关系数 r，首先值得注意的是它的符号．当 r 为正时，表明变量 x、y 正相关； 当 r 为负时，表明变量 x、y 负相关．反映在散点图上，图(1)中的变量 x、y 正相关，这时 的 r 为正；图(2)中的变量 x、y 负相关，这时的 r 为负． 另一个值得注意的是 r 的大小．统计学认为，对于变量 x、y，如果 r∈[－1，－0.75]， 那么负相关很强；如果 r∈[0.75,1]，那么正相关很强；如果 r∈(－0.75，－0.30]或 r∈[0.30,0.75)，那么相关性一般；如果 r∈[－0.25,0.25]，那么相关性较弱．反映在散 点图上，图(1)的 r＝0.97，这些点有明显的从左下角到右上角沿直线分布趋势，这时用线 性回归模型描述两个变量之间的关系效果很好；图(2)的 r＝－0.85，这些点也有明显的从 左上角到右下角沿直线分布趋势．这时用线性回归模型描述两个变量之间的关系也有好的效 果． 你能试着对自己身边的某个问题，确定两个变量，通过收集数据，计算相关系数，然后 分析一下能否用线性回归模型来拟合它们之间的关系吗？ 图(1) 图(2)