- 2021-05-21 发布 |
- 37.5 KB |
- 3页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
直线与圆的位置关系3
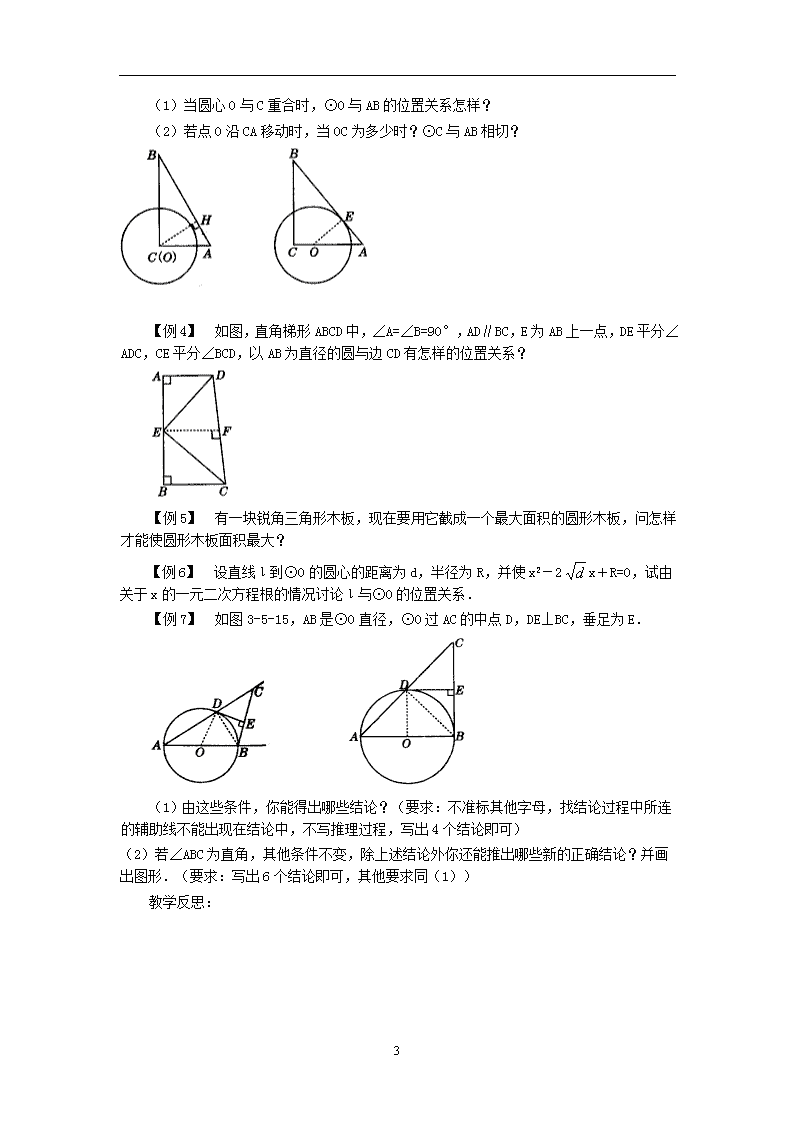
§27.2.2 直线与圆的位置关系1 学习目标: 经历探索直线和圆位置关系的过程,理解直线与圆有相交、相切、相离三种位置关系,了解切线的概念,探索切线与过切点的直径之间的关系。 学习重点: 直线和圆的三种位置关系,切线的概念和性质. 学习难点: 探索切线的性质. 学习方法: 教师指导学生探索法. 学习过程: 一、 举例: 【例1】在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,以C为圆心,r为半径的圆与AB有何位置关系?(1)r=2cm;(2)r=2.4cm(3)r=3cm. 【例2】已知:如图,△ABC中,内切圆I和边BC、CA、AB分别相切于点D、E、F,若∠FDE=70°,求∠A的度数. 【例3】小红家的锅盖坏了,为了配一个锅盖,需要测量锅的直径(铅沿所形成的圆的直径),而小红家只有一把长20cm的直尺,根本不够长,怎么办呢?小红想了想,采取了以下办法:如图,首先把锅平放到墙根,锅沿刚好靠到两墙,用直尺紧贴墙面量得MA的长,即可求出锅的直径.请你利用图说明她这样做的理由. 【例4】如图3-5-9,已知,求作:(1)确定的圆心;(2)过点A且与⊙O相切的直线.(注:作图要求利用直尺和圆规,不写作法,但要求保留作图痕迹) 3 【例5】 东海某小岛上有一灯塔A,已知A塔附近方圆25海里范围内有暗礁,我110舰在O点处测得A塔在其北偏西60°方向,向正西方向航行20海里到达B处,测得A在其西北方向.如果该舰继续航行,是否有触礁的危险?请说明理由.(提示=1.414,=1.732) 教学反思: §27.2.2 直线与圆的位置关系2 学习目标: 能判定一条直线是否为圆的切线,会过圆上一点画圆的切线,会作三角形的内切圆. 学习重点: 切线的判定和画法. 学习难点: 探索圆的切线的判定方法,作三角形内切圆的方法 学习方法: 师生共同探索法. 学习过程: 一、举例: 【例1】 如图,已知⊙O中,AB是直径,过B点作⊙O的切线BC,连结CO.若AD∥OC交⊙O于D.求证:CD是⊙O的切线. 【例2】 已知:如图,同心圆O,大圆的弦AB=CD,且AB是小圆的切线,切点为E.求证:CD是小圆的切线. 【例3】 如图,在Rt△ABC中,∠C=90°,AC=5,BC=12,⊙O的半径为3. 3 (1)当圆心O与C重合时,⊙O与AB的位置关系怎样? (2)若点O沿CA移动时,当OC为多少时?⊙C与AB相切? 【例4】 如图,直角梯形ABCD中,∠A=∠B=90°,AD∥BC,E为AB上一点,DE平分∠ADC,CE平分∠BCD,以AB为直径的圆与边CD有怎样的位置关系? 【例5】 有一块锐角三角形木板,现在要用它截成一个最大面积的圆形木板,问怎样才能使圆形木板面积最大? 【例6】 设直线ι到⊙O的圆心的距离为d,半径为R,并使x2-2x+R=0,试由关于x的一元二次方程根的情况讨论ι与⊙O的位置关系. 【例7】 如图3-5-15,AB是⊙O直径,⊙O过AC的中点D,DE⊥BC,垂足为E. (1)由这些条件,你能得出哪些结论?(要求:不准标其他字母,找结论过程中所连的辅助线不能出现在结论中,不写推理过程,写出4个结论即可) (2)若∠ABC为直角,其他条件不变,除上述结论外你还能推出哪些新的正确结论?并画出图形.(要求:写出6个结论即可,其他要求同(1)) 教学反思: 3查看更多