五年级上册数学教案-6组合图形面积｜冀教版 (1)

五年级上册数学教案-6组合图形面积｜冀教版 (1)

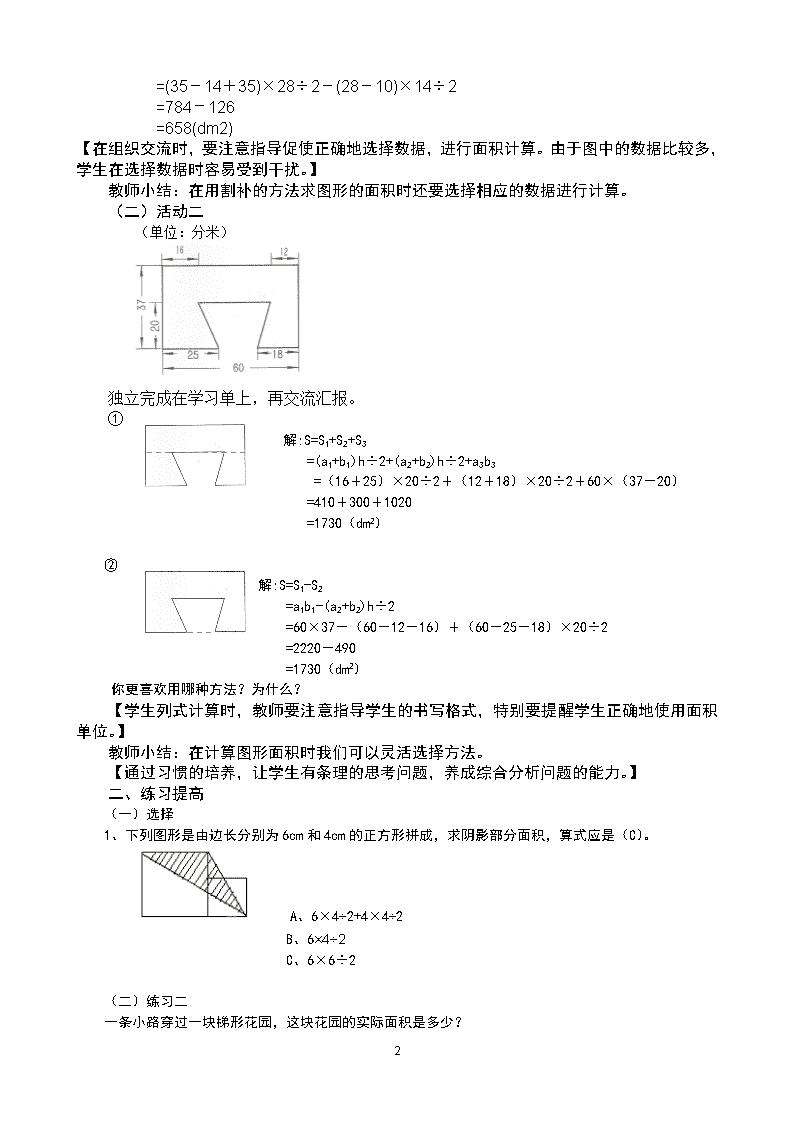
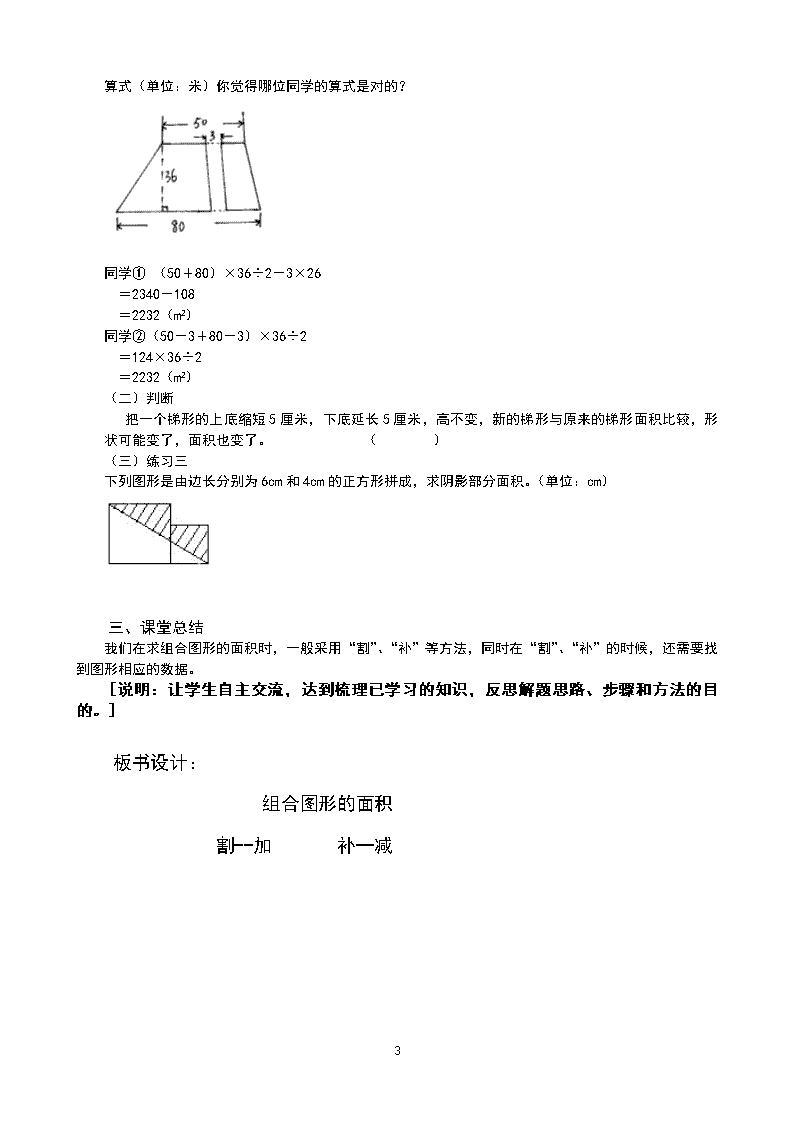
组合图形面积复习 ‎ 教学目标：‎ ‎1、能通过观察，弄清图形的组合关系。‎ ‎2、能通过割、补的方法求组合图形的面积。‎ 教学重点：‎ 能通过割、补的方法求组合图形的面积。‎ 教学难点：‎ ‎ 判断图形的组合关系，正确找出分割后图形的数据。‎ 教学准备：多媒体课件、学习单 教学过程：‎ 一、 复习巩固 ‎（一）活动一 ‎ 计算图形的面积，比一比谁的方法多。‎ ‎ （单位：分米）‎ （1） 这个图形的面积怎么求？‎ ‎ 请一位学生交流想法，并且将每个图形所对应的数据说出来。‎ ‎ 请全班将这一种方法写在学习单上。‎ ‎ （2）你们还有不同的方法来求这个图形的面积嘛？‎ ‎（同桌交流）先独立思考再和同桌交流你的方法，最后完成在学习单上，只列式，不计算。‎ ‎（3）独立完成 ‎（4）展示学习单，并由学生汇报 方法一： 解： S=S1＋S2‎ ‎ =a1b1＋a2b2÷2‎ ‎ =28×(35－14)＋14×10÷2‎ ‎ =588＋70‎ ‎ =658(dm2)‎ 方法二：解: S=S1＋S2‎ ‎ =a1b1+(a2+b2)h÷2‎ ‎ =(28－10)×(35－14)＋(35－14＋35)×10÷2‎ ‎ =378＋280‎ ‎ =658(dm2)‎ 方法三：‎ 解:S=S1-S2‎ ‎ =(a1+b1)h÷2-a2b2÷2‎ 3‎ ‎ =(35－14＋35)×28÷2－(28－10)×14÷2‎ ‎ =784－126‎ ‎ =658(dm2)‎ ‎【在组织交流时，要注意指导促使正确地选择数据，进行面积计算。由于图中的数据比较多，学生在选择数据时容易受到干扰。】‎ 教师小结：在用割补的方法求图形的面积时还要选择相应的数据进行计算。‎ ‎（二）活动二 ‎ （单位：分米）‎ 独立完成在学习单上，再交流汇报。‎ ‎①‎ ‎ 解:S=S1+S2+S3 ‎ ‎ =(a1+b1)h÷2+(a2+b2)h÷2+a3b3‎ ‎=（16＋25）×20÷2＋（12＋18）×20÷2＋60×（37－20）‎ ‎ =410＋300＋1020‎ ‎ =1730（dm2）‎ ‎②‎ ‎ 解:S=S1-S2‎ ‎ =a1b1-(a2+b2)h÷2‎ ‎=60×37－（60－12－16）＋（60－25－18）×20÷2‎ ‎ =2220－490‎ ‎ =1730（dm2）‎ ‎ 你更喜欢用哪种方法？为什么？‎ ‎【学生列式计算时，教师要注意指导学生的书写格式，特别要提醒学生正确地使用面积单位。】‎ 教师小结：在计算图形面积时我们可以灵活选择方法。‎ ‎【通过习惯的培养，让学生有条理的思考问题，养成综合分析问题的能力。】‎ 二、练习提高 ‎（一）选择 ‎1、下列图形是由边长分别为6cm和4cm的正方形拼成，求阴影部分面积，算式应是（C）。‎ ‎ A、6×4÷2+4×4÷2‎ B、6×4÷2‎ C、6×6÷2 ‎ ‎（二）练习二 一条小路穿过一块梯形花园，这块花园的实际面积是多少？‎ 3‎ 算式（单位：米）你觉得哪位同学的算式是对的？‎ 同学① （50＋80）×36÷2－3×26‎ ‎ ＝2340－108‎ ‎ ＝2232（m2）‎ 同学②（50－3＋80－3）×36÷2‎ ‎ ＝124×36÷2‎ ‎ ＝2232（m2）‎ （二） 判断 ‎ 把一个梯形的上底缩短5厘米，下底延长5厘米，高不变，新的梯形与原来的梯形面积比较，形状可能变了，面积也变了。 （ ）‎ ‎（三）练习三 下列图形是由边长分别为6cm和4cm的正方形拼成，求阴影部分面积。（单位：cm）‎ 三、课堂总结 我们在求组合图形的面积时，一般采用“割”、“补”等方法，同时在“割”、“补”的时候，还需要找到图形相应的数据。‎ ‎[说明：让学生自主交流，达到梳理已学习的知识，反思解题思路、步骤和方法的目的。]‎ 板书设计： ‎ 组合图形的面积 ‎ 割--加 补--减 3‎