中考冲刺数学专题

中考冲刺数学专题

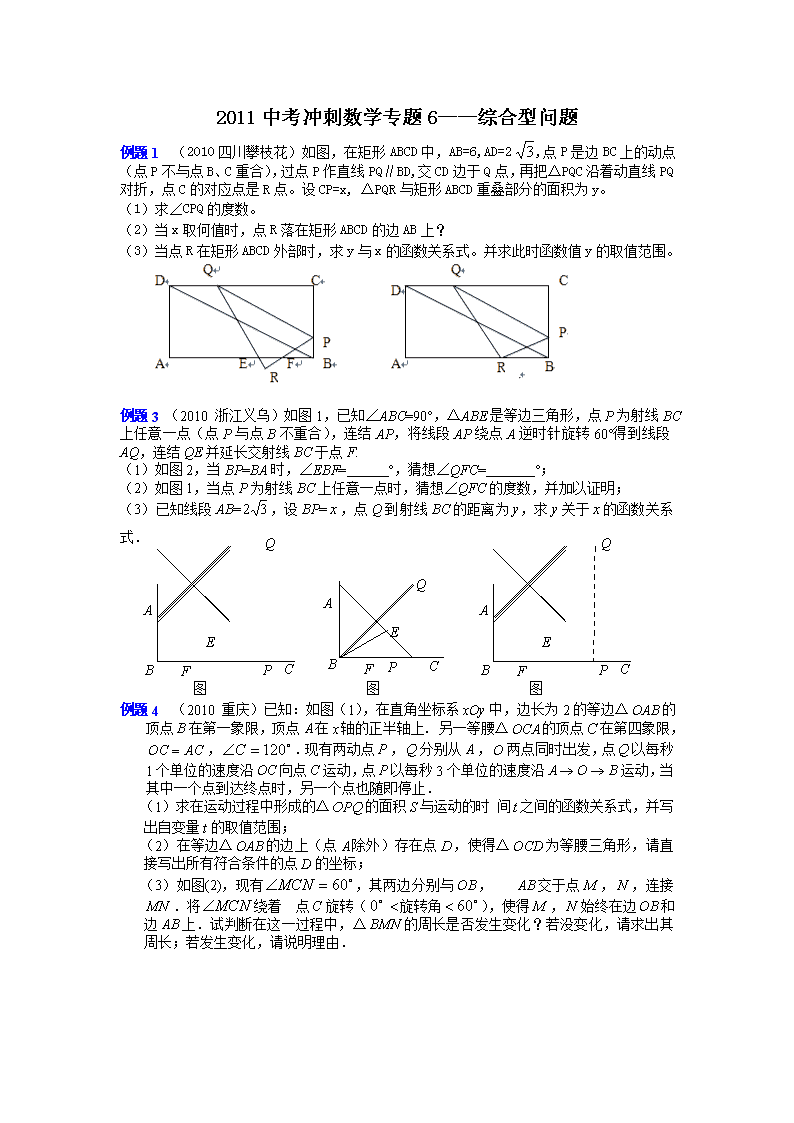
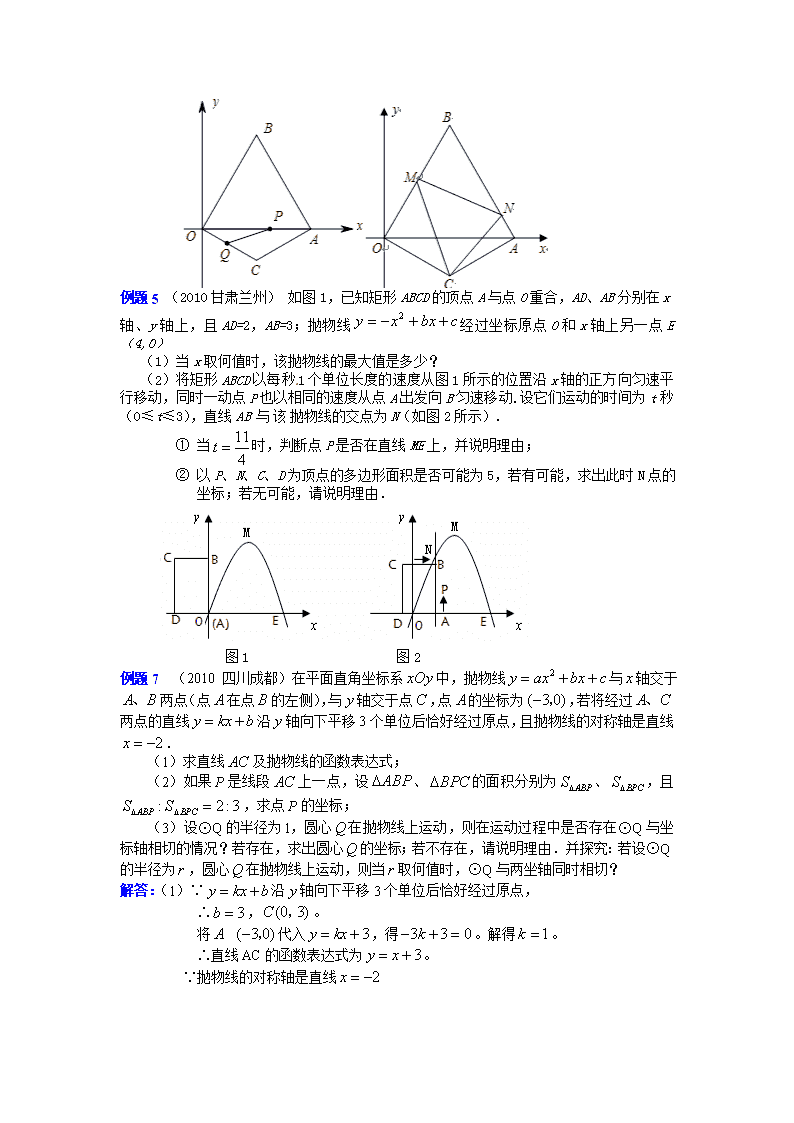
‎2011中考冲刺数学专题6——综合型问题 例题1 （2010四川攀枝花）如图，在矩形ABCD中，AB=6,AD=2,点P是边BC上的动点（点P不与点B、C重合），过点P作直线PQ∥BD,交CD边于Q点，再把△PQC沿着动直线PQ对折，点C的对应点是R点。设CP=x, △PQR与矩形ABCD重叠部分的面积为y。‎ ‎（1）求∠CPQ的度数。‎ ‎（2）当x取何值时，点R落在矩形ABCD的边AB上？‎ ‎（3）当点R在矩形ABCD外部时，求y与x的函数关系式。并求此时函数值y的取值范围。‎ 例题3 （2010 浙江义乌）如图1，已知∠ABC=90°，△ABE是等边三角形，点P为射线BC上任意一点（点P与点B不重合），连结AP，将线段AP绕点A逆时针旋转60°得到线段AQ，连结QE并延长交射线BC于点F.‎ ‎（1）如图2，当BP=BA时，∠EBF=　 　°，猜想∠QFC= °；‎ ‎（2）如图1，当点P为射线BC上任意一点时，猜想∠QFC的度数，并加以证明；‎ 图1‎ A C B E Q F P 图2‎ A B E Q P F C 图1‎ A C B E Q F P ‎（3）已知线段AB=，设BP=，点Q到射线BC的距离为y，求y关于的函数关系式．‎ 例题4 （2010 重庆）已知：如图（1），在直角坐标系xOy中，边长为2的等边△的顶点在第一象限，顶点在轴的正半轴上. 另一等腰△的顶点在第四象限，，．现有两动点，分别从，两点同时出发，点以每秒1个单位的速度沿向点运动，点以每秒3个单位的速度沿运动，当其中一个点到达终点时，另一个点也随即停止．‎ ‎（1）求在运动过程中形成的△的面积与运动的时 间之间的函数关系式，并写出自变量t的取值范围；‎ ‎（2）在等边△的边上（点除外）存在点，使得△为等腰三角形，请直接写出所有符合条件的点D的坐标；‎ ‎（3）如图(2)，现有，其两边分别与， 交于点，，连接．将绕着 点旋转（旋转角），使得，始终在边和边上．试判断在这一过程中，△的周长是否发生变化？若没变化，请求出其周长；若发生变化，请说明理由．‎ 例题5 （2010甘肃兰州） 如图1，已知矩形ABCD的顶点A与点O重合，AD、AB分别在x轴、y轴上，且AD=2，AB=3；抛物线经过坐标原点O和x轴上另一点E（4,0）‎ ‎（1）当x取何值时，该抛物线的最大值是多少？‎ ‎（2）将矩形ABCD以每秒1个单位长度的速度从图1所示的位置沿x轴的正方向匀速平行移动，同时一动点P也以相同的速度从点A出发向B匀速移动.设它们运动的时间为t秒（0≤t≤3），直线AB与该抛物线的交点为N（如图2所示）. ‎ ‎① 当时，判断点P是否在直线ME上，并说明理由；‎ ‎② 以P、N、C、D为顶点的多边形面积是否可能为5，若有可能，求出此时N点的坐标；若无可能，请说明理由．‎ 图1 图2‎ 例题7 （2010 四川成都）在平面直角坐标系中，抛物线与轴交于两点（点在点的左侧），与轴交于点，点的坐标为，若将经过两点的直线沿轴向下平移3个单位后恰好经过原点，且抛物线的对称轴是直线．‎ ‎（1）求直线及抛物线的函数表达式；‎ ‎（2）如果P是线段上一点，设、的面积分别为、，且，求点P的坐标；‎ ‎（3）设⊙Q的半径为l，圆心在抛物线上运动，则在运动过程中是否存在⊙Q与坐标轴相切的情况？若存在，求出圆心的坐标；若不存在，请说明理由．并探究：若设⊙Q的半径为，圆心在抛物线上运动，则当取何值时，⊙Q与两坐轴同时相切？‎ 解答：（1）∵沿轴向下平移3个单位后恰好经过原点，‎ ‎ ∴，。‎ ‎ 将 代入，得。解得。‎ ‎ ∴直线AC的函数表达式为。‎ ‎ ∵抛物线的对称轴是直线 ‎∴解得 ‎∴抛物线的函数表达式为。‎ ‎（2）如图，过点B作BD⊥AC于点D。‎ ‎ ‎ ‎∵，‎ ‎∴ ‎ ‎∴。‎ 过点P作PE⊥x轴于点E，‎ ‎∵PE∥CO，∴△APE∽△ACO，‎ ‎∴，‎ ‎∴‎ ‎∴，解得 ‎∴点P的坐标为 ‎（3）（Ⅰ）假设⊙Q在运动过程中，存在与坐标轴相切的情况。‎ ‎ 设点Q的坐标为。‎ ① 当⊙Q与y轴相切时，有，即。‎ 当时，得，∴‎ 当时，得，∴‎ ② 当⊙Q与x轴相切时，有，即 当时，得，即，解得，∴‎ 当时，得，即，解得，∴，。‎ 综上所述，存在符合条件的⊙Q，其圆心Q的坐标分别为，，，，。‎ ‎（Ⅱ）设点Q的坐标为。‎ 当⊙Q与两坐标轴同时相切时，有。‎ 由，得，即，‎ ‎∵△=‎ ‎∴此方程无解。‎ 由，得，即，‎ 解得 ‎∴当⊙Q的半径时，⊙Q与两坐标轴同时相切。‎ 例题8 （2010湖南常德）如图, 已知抛物线与轴交于A (－4，0) 和B(1，0)两点，与轴交于C点．‎ ‎（1）求此抛物线的解析式；‎ ‎（2）设E是线段AB上的动点，作EF//AC交BC于F，连接CE，当△CEF的面积是△BEF面积的2倍时，求E点的坐标;‎ ‎（3）若P为抛物线上A、C两点间的一个动点，过P作轴的平行线，交AC于Q，当P点运动到什么位置时，线段PQ的值最大，并求此时P点的坐标．‎ 解答：（1）由二次函数与轴交于、两点可得：‎ ‎　　　　　　　解得：　‎ ‎　　　　故所求二次函数的解析式为． ‎ ‎（2）∵S△CEF=2 S△BEF, ∴ ‎ ‎ ∵EF//AC, ∴,‎ ‎ ∴△BEF～△BAC, ‎ ‎∴得 ‎ 故E点的坐标为(,0). ‎ ‎　　　（3）解法一：由抛物线与轴的交点为，则点的坐标为（0，－2）．若设直线的解析式为，则有　解得： ‎ 故直线的解析式为． ‎ 若设点的坐标为，又点是过点所作轴的平行线与直线的交点，则点的坐标为（．则有：‎ ‎　　　　　　　＝‎ ‎＝‎ 即当时，线段取大值，此时点的坐标为（－2，－3）‎ 解法二：延长交轴于点，则．要使线段最长，则只须△的面积取大值时即可. ‎ 设点坐标为（，则有: ‎ ‎　　　 ‎ ‎ 　 ＝‎ ‎　 ＝‎ ‎ ＝‎ ‎＝‎ ‎＝ ＝－‎ 即时，△的面积取大值，此时线段最长，则点坐标为（－2，－3） ‎ ‎【技巧提炼】‎ 解数学综合题，一要树立必胜的信心，二要具备扎实的基础知识和熟练的基本技能，三要掌握常用的解题策略。现介绍几种常用的解题策略，供初三同学参考。‎ ‎1、 以坐标系为桥梁，运用数形结合思想 纵观最近几年各地的中考压轴题，绝大部分都是与坐标系有关的，其特点是通过建立点与数即坐标之间的对应关系，一方面可用代数方法研究几何图形的性质，另一方面又可借助几何直观，得到某些代数问题的解答。‎ ‎2、 以直线或抛物线知识为载体，运用函数与方程思想 直线与抛物线是初中数学中的两类重要函数，即一次函数与二次函数所表示的图形。因此，无论是求其解析式还是研究其性质，都离不开函数与方程的思想。例如函数解析式的确定，往往需要根据已知条件列方程或方程组并解之而得。‎ ‎3、 利用条件或结论的多变性，运用分类讨论的思想 分类讨论思想可用来检测学生思维的准确性与严密性，常常通过条件的多变性或结论的不确定性来进行考察，有些问题，如果不注意对各种情况分类讨论，就有可能造成错解或漏解，纵观近几年的中考压轴题分类讨论思想解题已成为新的热点。‎ ‎4、 综合多个知识点，运用等价转换思想 任何一个数学问题的解决都离不开转换的思想，初中数学中的转换大体包括由已知向未知，由复杂向简单的转换，而作为中考压轴题，更注意不同知识之间的联系与转换，一道中考压轴题一般是融代数、几何、三角于一体的综合试题，转换的思路更要得到充分的应用。‎ ‎【体验中考】‎ ‎1．（2010 福建德化）已知：如图，点是正方形的对角线上的一个动点(、除外)，作于点，作于点，设正方形的边长为，矩形的周长为，在下列图象中，大致表示与之间的函数关系的是（ ）. ‎ x y ‎0‎ A x y ‎0‎ D x y ‎0‎ B y x ‎0‎ C P D A B C C E F ‎2．（2010 四川南充）如图，直线l1∥l2，⊙O与l1和l2分别相切于点A和点B．点M和点N分别是l1和l2上的动点，MN沿l1和l2平移．⊙O的半径为1，∠1＝60°．下列结论错误的是（　　）． l1‎ l2‎ A B M N O ‎1‎ （A） （B）若MN与⊙O相切，则 （C）若∠MON＝90°，则MN与⊙O相切 （D）l1和l2的距离为2 ‎ ‎3．（2010湖北鄂州）如图所示，四边形OABC为正方形，边长为6，点A、C分别在x轴，y轴的正半轴上， 点Ｄ在OA上，且Ｄ点的坐标为（2，0），P是OB上的一个动点，试求PD+PA和的最小值是（ ）‎ A．　　　B．　　C．4　　　D．6‎ ‎4．（2010湖北宜昌）如图,在圆心角为90°的扇形MNK中，动点P从点M出发，沿MNKM运动，最后回到点M的位置。设点P运动的路程为x，P与M两点之间的距离为y，其图象可能是（ ）。‎ ‎5．（2010湖南怀化）图9是二次函数的图象，其顶点坐标为M(1,-4).‎ ‎（1）求出图象与轴的交点A,B的坐标； ‎ ‎（2）在二次函数的图象上是否存在点P，使,若存在，求出P点的 坐标；若不存在，请说明理由；‎ ‎（3）将二次函数的图象在轴下方的部分沿轴翻折，图象的其余部分保持不变，‎ 得到一个新的图象，请你结合这个新的图象回答：当直线与此 图象有两个公共点时，的取值范围.‎ ‎ ‎ ‎6．（2010湖北鄂州）如图，在直角坐标系中，A（-1，0），B（0，2），一动点P沿过B点且垂直于AB的射线BM运动，P点的运动速度为每秒1个单位长度，射线BM与x轴交与点C．‎ ‎（1）求点C的坐标．‎ ‎（2）求过点A、B、C三点的抛物线的解析式．‎ ‎（3）若P点开始运动时，Q点也同时从C出发，以P点相同的速度沿x轴负方向向点A运动，t秒后，以P、Q、C为顶点的三角形为等腰三角形．（点P到点C时停止运动，点Q也同时停止运动）求t的值．‎ ‎（4）在（2）（3）的条件下，当CQ=CP时，求直线OP与抛物线的交点坐标．‎ ‎7．（2010湖北荆州）如图，直角梯形OABC的直角顶点O是坐标原点，边OA，OC分别在x轴、y轴的正半轴上，OA∥BC，D是BC上一点，BD=OA=，AB=3，∠OAB=45°，E、F分别是线段OA、AB上的两动点，且始终保持∠DEF=45°．‎ ‎（1）直接写出D点的坐标；‎ ‎（2）设OE=x，AF=y，试确定y与x之间的函数关系；‎ ‎（3）当△AEF是等腰三角形时，将△AEF沿EF折叠，得到△，求△与五边形OEFBC重叠部分的面积．‎ ‎8．（2010湖北省咸宁）如图，直角梯形ABCD中，AB∥DC，，，．动点M以每秒1个单位长的速度，从点A沿线段AB向点B运动；同时点P以相同的速度，从点C沿折线C-D-A向点A运动．当点M到达点B时，两点同时停止运动．过点M作直线l∥AD，与线段CD的交点为E，与折线A-C-B的交点为Q．点M运动的时间为t（秒）． 全品中考网 ‎（1）当时，求线段的长；‎ ‎（2）当0＜t＜2时，如果以C、P、Q为顶点的三角形为直角三角形，求t的值；‎ ‎（3）当t＞2时，连接PQ交线段AC于点R．请探究是否为定值，若是，试求这个定值；若不是，请说明理由．‎ A B C D ‎（备用图1）‎ A B C D ‎（备用图2）‎ Q A B C D l M P E ‎9．（2010江苏扬州）在△ABC中，∠C＝90°，AC＝3，BC＝4，CD是斜边AB上的高，点E在斜边AB上，过点E作直线与△ABC的直角边相交于点F，设AE＝x，△AEF的面积为y．‎ ‎（1）求线段AD的长；‎ ‎（2）若EF⊥AB，当点E在线段AB上移动时，①求y与x的函数关系式（写出自变量x的取值范围）②当x取何值时，y有最大值？并求其最大值；‎ ‎（3）若F在直角边AC上（点F与A、C两点均不重合），点E在斜边AB上移动，试问：是否存在直线EF将△ABC的周长和面积同时平分？若存在直线EF，求出x的值；若不存在直线EF，请说明理由．‎ 答案 ‎1．【答案】A ‎ ‎2．【答案】B ‎ ‎3．【答案】A ‎ ‎4．【答案】B ‎ ‎5．【答案】(1) 因为M(1,-4) 是二次函数的顶点坐标，‎ 所以 ‎ 令解之得.‎ ‎∴A，B两点的坐标分别为A（-1，0），B（3,0）‎ ‎(2) 在二次函数的图象上存在点P，使 设则，‎ 又,‎ ‎∴‎ ‎∵二次函数的最小值为-4，∴.‎ 当时，.‎ 故P点坐标为（-2，5）或（4，5）‎ ‎（3）如图1，当直线经过A点时，可得 ‎ 当直线经过B点时，可得 由图可知符合题意的的取值范围为 ‎6．【答案】‎ ‎（1）点C的坐标是（4，0）；‎ ‎（2）设过点A、B、C三点的抛物线的解析式为y=ax2+bx+c（a≠0），将点A、B、C三点的坐标代入得：‎ 解得，∴抛物线的解析式是：y= x2+x+2．‎ ‎（3）设P、Q的运动时间为t秒，则BP=t，CQ=t．以P、Q、C为顶点的三角形为等腰三角形，可分三种情况讨论．‎ ‎①若CQ=PC，如图所示，则PC= CQ=BP=t．∴有2t=BC=，∴t=．‎ ‎②若PQ=QC，如图所示，过点Q作DQ⊥BC交CB于点D，则有CD=PD．由△ABC∽△QDC，可得出PD=CD=，∴，解得t=．‎ ‎③若PQ=PC，如图所示，过点P作PE⊥AC交AC于点E，则EC=QE=PC，∴t=（-t），解得t=．‎ ‎（4）当CQ=PC时，由（3）知t=，∴点P的坐标是（2，1），∴直线OP的解析式是：y=x，因而有x =x2+x+2，即x2-2x-4=0，解得x=1±，∴直线OP与抛物线的交点坐标为（1+，）和（1-，）．‎ ‎7．【答案】（1）D点的坐标是.‎ ‎（2）连结OD,如图（1），‎ 由结论（1）知：D在∠COA的平分线上，则 ‎∠DOE=∠COD=45°,又在梯形DOAB中，∠BAO=45°,∴OD=AB=3‎ 由三角形外角定理得：∠1=∠DEA-45°,又∠2=∠DEA-45°‎ ‎∴∠1=∠2, ∴△ODE∽△AEF ‎∴，即：‎ ‎∴y与x的解析式为：‎ ‎（3）当△AEF为等腰三角形时，存在EF=AF或EF=AE或AF=AE共3种情况.‎ ① 当EF=AF时，如图（2）.‎ ‎∠FAE=∠FEA=∠DEF=45°,‎ ‎∴△AEF为等腰直角三角形.D在A’E上（A’E⊥OA）,‎ B在A’F上（A’F⊥EF）‎ ‎∴△A’EF与五边形OEFBC重叠的面积为 四边形EFBD的面积.‎ ‎∵‎ ‎∴‎ ‎∴‎ ‎∴（也可用）‎ ‎ ‎ ‎②当EF=AE时，如图（3），‎ 此时△A’EF与五边形OEFBC重叠部分面积为△A’EF面积.‎ ‎∠DEF=∠EFA=45°， DE∥AB ， 又DB∥EA ‎∴四边形DEAB是平行四边形 ‎∴AE=DB=‎ ‎∴‎ ‎③当AF=AE时，如图（4），四边形AEA’F为菱形且△A’EF在五边形OEFBC内.‎ ‎ ∴此时△A’EF与五边形OEFBC重叠部分面积为△A’EF面积.‎ ‎ ‎ 由（2）知△ODE∽△AEF,则OD=OE=3‎ ‎ ∴AE=AF=OA-OE=‎ ‎ 过F作FH⊥AE于H,则 ‎∴‎ 综上所述，△A’EF与五边形OEFBC重叠部分的面积为或1或 ‎8．【答案】（1）过点C作于F，则四边形AFCD为矩形．‎ ‎∴，．‎ Q A B C D l M P E F 此时，Rt△AQM∽Rt△ACF．‎ ‎∴．‎ 即，∴．‎ ‎（2）∵为锐角，故有两种情况：‎ ‎①当时，点P与点E重合．‎ A B C D ‎（备用图1）‎ Q P E l M 此时，即，∴．‎ ‎②当时，如备用图1，‎ 此时Rt△PEQ∽Rt△QMA，∴．‎ 由（1）知，，‎ 而，‎ ‎∴． ∴．‎ 综上所述，或．‎ ‎（3）为定值．‎ 当＞2时，如备用图2，‎ A B C D ‎（备用图2）‎ M Q R F P ‎．‎ 由（1）得，．‎ ‎∴． ∴．‎ ‎∴． ∴．‎ ‎∴四边形AMQP为矩形． ∴∥．‎ ‎∴△CRQ∽△CAB．‎ ‎∴．‎ ‎9．【答案】（1）∵AC=3，BC=4‎ ‎∴AB=5‎ ‎∵AC·BC=AB·CD，‎ ‎∴CD=，AD=‎ ‎ （2）①当0＜x≤时 ‎ ∵EF∥CD ‎∴△AEF∽△ADC ‎∴‎ 即EF=x ‎∴y=·x·x=‎ ‎ 当＜x≤5时 ‎ 易得△BEF∽△BDC，同理可求EF=（5—x）‎ ‎ ∴y=·x·（5—x）=≤‎ ‎②当0＜x≤时，y随x的增大而增大.‎ y=≤,即当x=时，y最大值为 ‎ 当＜x≤5时，‎ ‎ ∵‎ ‎ ∴当时，y的最大值为 ‎ ∵＜‎ ‎ ∴当时，y的最大值为 ‎（3）假设存在 ‎ 当0＜x≤5时，AF=6—x ‎ ∴0＜6—x＜3‎ ‎ ∴3＜x＜6‎ ‎ ∴3＜x≤5‎ ‎ 作FG⊥AB与点G ‎ 由△AFG∽△ACD可得 ‎ ∴，即FG=‎ ‎ ∴x·=‎ ‎ ∴=3，即2x2-12x+5=0‎ ‎ 解之得x1=，x2=‎ ‎ ∵3＜x1≤5‎ ‎ ∴x1=符合题意 ‎ ∵x2=＜3‎ ‎ ∴x2不合题意，应舍去 ‎ ∴存在这样的直线EF，此时，x=‎