- 2021-05-12 发布 |
- 37.5 KB |
- 4页

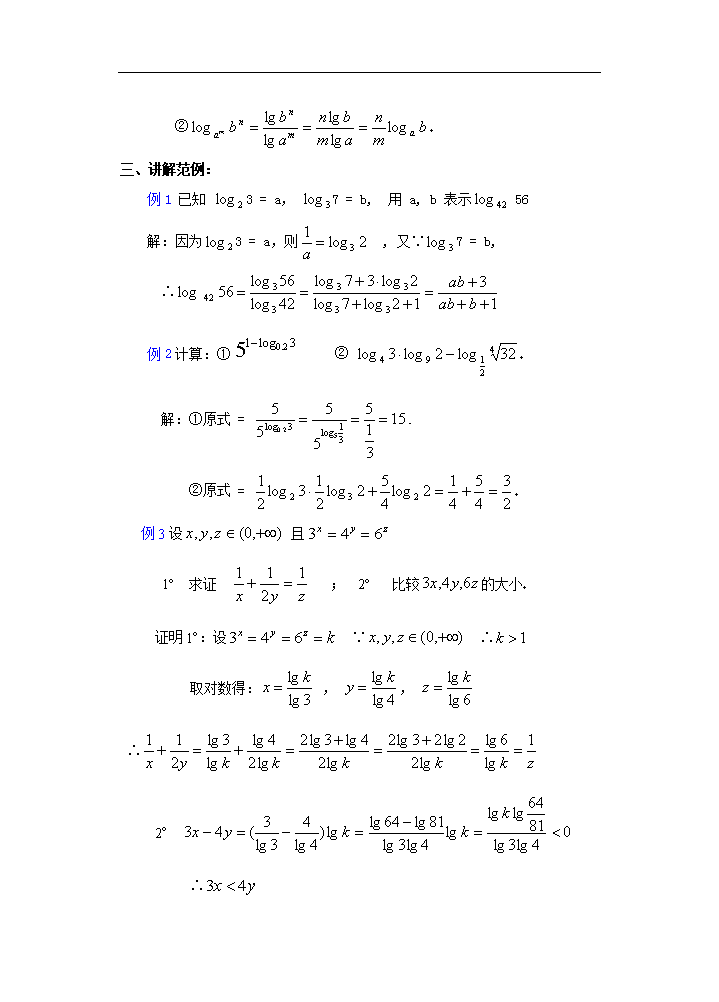

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高中数学必修1教案:第二章(第19课时)对数3
课 题:2.7.3 对数的换底公式及其推论 教学目的: 1.掌握对数的换底公式,并能解决有关的化简、求值、证明问题 2.培养培养观察分析、抽象概括能力、归纳总结能力、逻辑推理能力; 教学重点:换底公式及推论 教学难点:换底公式的证明和灵活应用. 授课类型:新授课 课时安排:1课时 教 具:多媒体、实物投影仪 教学过程: 一、复习引入:对数的运算法则 如果 a > 0,a ¹ 1,M > 0, N > 0 有: 二、新授内容: 1.对数换底公式: ( a > 0 ,a ¹ 1 ,m > 0 ,m ¹ 1,N>0) 证明:设 N = x , 则 = N 两边取以m 为底的对数: 从而得: ∴ 2.两个常用的推论: ①, ② ( a, b > 0且均不为1) 证:① ② 三、讲解范例: 例1 已知 3 = a, 7 = b, 用 a, b 表示 56 解:因为3 = a,则 , 又∵7 = b, ∴ 例2计算:① ② 解:①原式 = ②原式 = 例3设 且 1° 求证 ; 2° 比较的大小 证明1°:设 ∵ ∴ 取对数得: , , ∴ 2° ∴ 又: ∴ ∴ 例4已知x=c+b,求x 分析:由于x作为真数,故可直接利用对数定义求解;另外,由于等式右端为两实数和的形式,b的存在使变形产生困难,故可考虑将c移到等式左端,或者将b变为对数形式 解法一: 由对数定义可知: 解法二: 由已知移项可得 ,即 由对数定义知: 解法三: 四、课堂练习: ①已知 9 = a , = 5 , 用 a, b 表示45 解:∵ 9 = a ∴ ∴2 = 1-a ∵ = 5 ∴ 5 = b ∴ ②若3 = p , 5 = q , 求 lg 5 解:∵ 3 = p ∴ =p 又∵ ∴ 三、小结 本节课学习了以下内容:换底公式及其推论 四、课后作业: 1.证明: 证法1: 设 ,, 则: ∴ 从而 ∵ ∴ 即:(获证) 证法2: 由换底公式 左边==右边 2.已知 求证: 证明:由换底公式 由等比定理得: ∴ ∴ 五、板书设计(略) 六、课后记:查看更多