- 2021-05-11 发布 |
- 37.5 KB |
- 3页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高中数学第二章基本初等函数Ⅰ2_2对数函数第3课时课堂探究学案新人教A版必修11
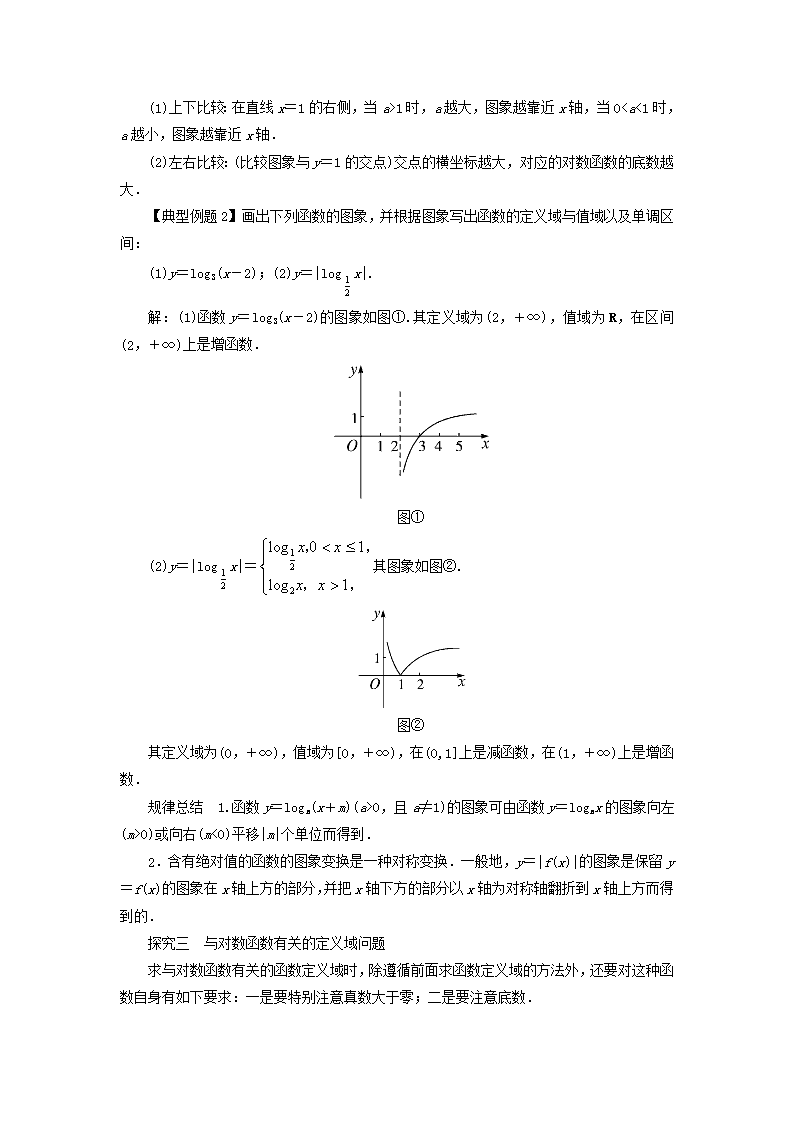
2.2 对数函数 课堂探究 探究一 对数函数的概念 判断一个函数是对数函数必须是形如 y=logax(a>0,且 a≠1)的形式,即必须满足以下 条件: (1)系数为 1. (2)底数为大于 0 且不等于 1 的常数. (3)对数的真数仅有自变量 x. 【典型例题 1】 下列函数中,哪些是对数函数? (1)y=logax2(a>0,且 a≠1); (2)y=log2x-1; (3)y=2log8x; (4)y=logxa(x>0,且 x≠1); (5)y=log5x. 思路分析:根据对数函数的定义进行判断. 解:只有(5)为对数函数. (1)中真数不是自变量 x,故不是对数函数; (2)中对数式后减 1,故不是对数函数; (3)中 log8x 前的系数是 2,而不是 1, 故不是对数函数; (4)中底数是自变量 x,而非常数 a,故不是对数函数. 探究二 对数函数的图象问题 1.画对数函数 y=logax 的图象时,应牢牢抓住三个关键点(a,1),(1,0), 1 , 1a . 2.对数函数图象与直线 y=1 的交点横坐标越大,则对应的对数函数的底数越大. 3.函数 y=logax(a>0,且 a≠1)的底数变化对图象位置的影响 观察图象,注意变化规律: (1)上下比较:在直线 x=1 的右侧,当 a>1 时,a 越大,图象越靠近 x 轴,当 0查看更多