- 2021-05-11 发布 |
- 37.5 KB |
- 17页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高中数学:《平行线分线段成比例》课件(新人教A版选修4-1)
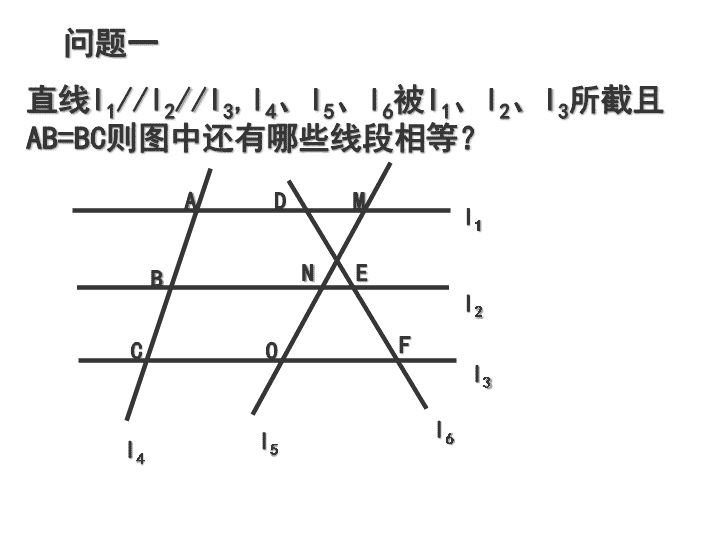
课题:平行线分线段成比例定理 l 1 l 3 l 2 l 4 l 5 l 6 A B C D E F M N O 直线 l 1 //l 2 //l 3 ,l 4 、 l 5 、 l 6 被 l 1 、 l 2 、 l 3 所截且 AB=BC 则图中还有哪些线段相等? 问题一 问题二 如何不通过测量,运用所学知识,快速将一根绳子分成两部分,使这两部分之比是 2:3? A B C ? E D F B I D I C I E I F I 3 2 C I F I 则 = AC I A B C E D F B I D I C I E I F I 3 2 = C I F I AC I CF A C = 3 1 = C I F I B I C I CF B C = BF B C 4 1 B I F I = B I C I = A B C E D F B I D I C I E I F I A B C E D F B I A I D I C I E I F I AD D F 3 2 A I D I = D I F I = AF D F 5 2 A I F I = D I F I = 平行线分线段成比例定理: 三条平行线截两条直线,所得的 线段 成比例 . 对应 怎样用文字把以上发现表述出来? A B C D E F l 1 l 3 l 2 . . . . . . . . 形象记忆 A B C D E F l 1 l 3 l 2 3 ? 4 2 [ 例一 ] (平行线分线段成比例 定理) 6 BC = 4 2 BC 3 即 = EF DE BC AB = //l //l l 解: 3 2 1 Q A B C D E F l 1 l 3 l 2 [ 例二 ] 注意观察: 此图与前面图形有何不同? A B C D E F (平行线分线段成比例定理) . n m m DF DE + = . m n m DE DF 即 + = , m m n DE DE EF + = + m n DE EF = n m EF DE BC AB = = , //l //l l 3 2 1 Q : 证明 A B C D E F A B C D E F A B C D E F A B C D E F A B C D E F A B C D E F l 1 l 3 l 2 ? [ 练习一 ] 求: DE. c. EF b, BC a, , AB //l //l 已知:如图, l 3 2 1 = = = l 1 l 3 l 2 [ 练习二 ] A B C D E F DE AB 求证: //l //l 已知:如图, l 3 2 1 = EF BC = DF AC 如图,有一块形状为直角梯形的草地,周围均为水泥直道,两个拐角 A 、 B 处均为直角,草地中间另有一条水泥直道 EF 垂直于 AB ,垂足为 E. 已知 AE 长 a 米, EB 长 b 米, DF 长 c 米 . 求 CF. A B C D E F a b c ? 米 . a bc 答: CF 长为 a bc CF CF c b a 即 定理) (平行线分线段成比例 CF DF EB AE AD//EF//BC B , EF 90 ABC DAB 解:由题意可知: 0 = = = ^ = Ð = Ð A 对题目的再思考 ! C F A B D E 若是三角形草地呢?( EF//BC ) 定理还能用吗? A B E C F 如上图: AE=3 , AF=6 , EB=4. 求 FC. 6 3 4 ? 8 三条平行线截两条直线,所得的 对应线段 成比例 . 平行线分线段成比例定理与平行线等分线段 定理有何联系? A B C D E F A B C D E F 结论:后者是前者的一种特殊情况! 平行线分线段成比例定理: 课 堂 小 结 要熟悉该定理的几种基本图形 A B C D E F A B C D E F A B C D E F A B C D E F A B C D E A B C D E 课后思考题 如图:若 AB//CD , 平行线分线段成比例定理 还能用吗? A B C D E查看更多