- 2021-05-12 发布 |
- 37.5 KB |
- 14页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
5年级数学教案《公因数和最大公因数练习》
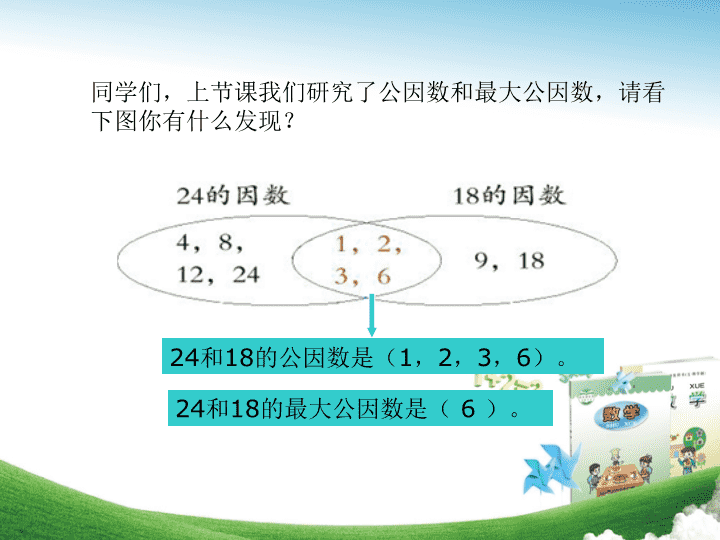
公因数和 最大公因数练习 五年级数学下册 分层练习,巩固提高 梳理总结,提升新知 问题回顾,再现新知 同学们,上节课我们研究了公因数和最大公因数,请看下图你有什么发现? 24 和 18 的公因数是( 1 , 2 , 3 , 6 )。 24 和 18 的最大公因数是( 6 )。 两个非零自然数公有的因数叫做它们的公因数。 1 其实是任意两个非零自然数的最小公因数。 任意一个非零自然数因数的个数是有限的,同样任意两个非零自然数的公因数的个数也是有限的 。 公因数的个数是有限的,所以有最大的公因数。我们就将其中那个最大的公因数叫做这两个数的最大公因数。 ◆ 问题回顾,再现新知 找两个非零自然数最大公因数的方法: ①可以用集合图的形式找最大公因数。 ②可以用列举的方法。 ③可以用短除法求最大公因数。 a. 每次除时都要用两个数的公有的因数去除。 b. 一直除到公因数只有 1 为止。 c. 最后写结论时要把所有的公因数(除数)连 乘起来,就可以得到这两个数的最大公因数。 ◆ 问题回顾,再现新知 在集合图里填上合适的数。 16 的因数 1 、 2 、 4 、 8 、 16 、 28 的因数 1 、 2 、 4 、 7 、 14 、 28 、 16 和 2 8 公有的因数 16 和 28 的最大公因数( )。 4 ◆基本练习,巩固新知 42 的因数 36 的因数 4 、 3 、 2 、 1 、 6 、 9 、 12 、 18 、 36 1 、 2 、 3 、 6 、 7 、 14 、 21 、 42 36 和 42 公有的因数 36 和 42 的最大公因数( )。 6 ◆基本练习,巩固新知 用列举法找出每组数的最大公因数。 4 和 10 12 和 18 24 和 30 35 和 63 最大公因数( ) 最大公因数( ) 最大公因数( ) 最大公因数( ) 2 6 6 7 ◆基本练习,巩固新知 4 的因数: 1 、 2 、 4 10 的因数: 1 、 2 、 5 、 10 4 和 10 的公因数: 1 、 2 用短除法求下列每组数的最大公因数。 18 和 32 最大公因数( ) 24 和 36 最大公因数( ) 14 和 21 最大公因数( ) 30 和 40 最大公因数( ) 56 和 28 最大公因数( ) 51 和 69 最大公因数( ) 2 12 7 10 28 3 ◆基本练习,巩固新知 18 32 2 9 16 先分别找出每组数的最大公因数,再仔细观察,你发现了什么? 6 和 12 8 和 9 18 和 54 24 和 72 17 和 28 15 和 32 1 6 18 1 24 1 较小的那个数。 它们的公因数是 1 。 ◆综合练习,应用新知 直接说出下面每组数的最大公因数。 5 和 20 7 和 24 6 和 18 6 和 16 30 和 6 7 和 16 ◆综合练习,应用新知 5 1 6 6 1 2 你能找出下面每个分数中分子与分母的最大公因数吗? 8 5 11 17 1 15 ◆综合练习,应用新知 实验小学用地板砖铺设长 90 分米、 宽 60 分米的微机室地面(如图)。 (1)从不浪费材料的角度考虑(使用的地板砖都是整块),可以选择边长是多少分米的正方形地板砖? (2)你认为选用边长是多少分米的地板砖比较合适?说说理由。 ◆拓展练习,发展新知 把 3 种彩条截成同样长的小段且没有剩余,每段彩条最长几厘米? 就是求 … 16 、 32 、 56 的最大公因数。 ◆拓展练习,发展新知 说一说这节课你都有哪些收获呢? 我的收获: ◆梳理总结,提升新知查看更多