- 2021-05-12 发布 |
- 37.5 KB |
- 17页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
全国统一高考数学试卷文科新课标及解析
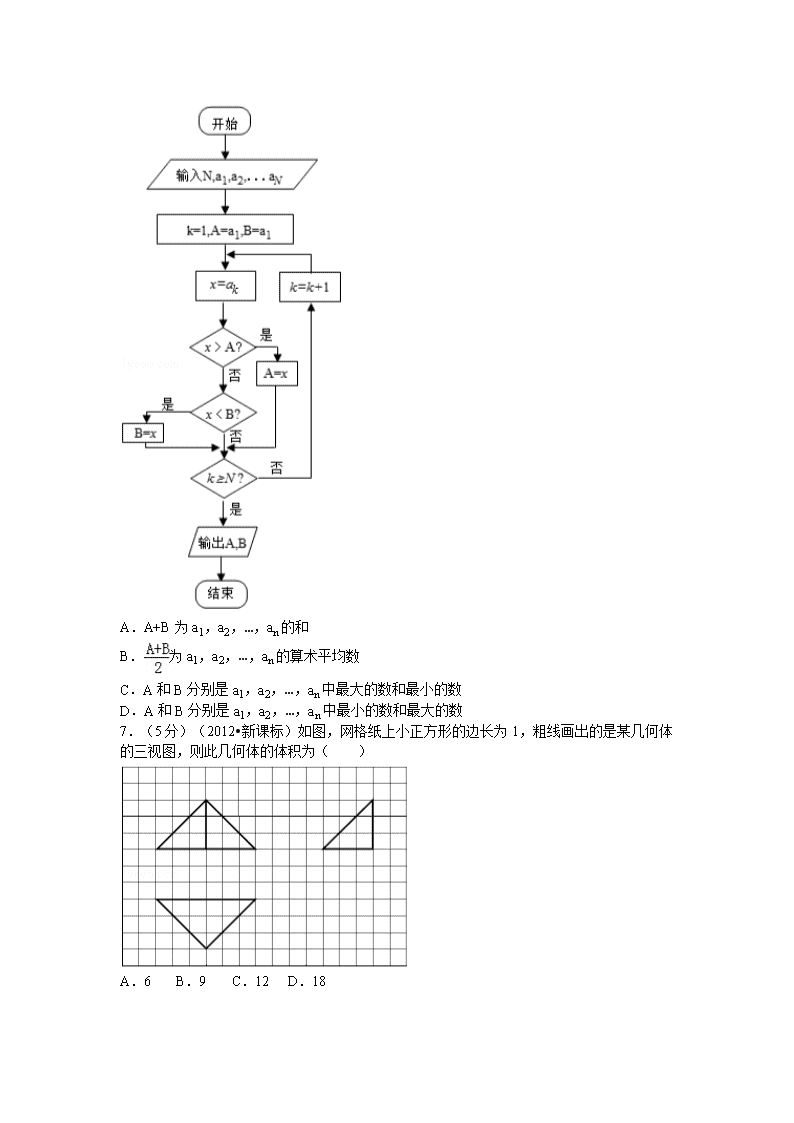
2012年全国统一高考数学试卷(文科)(新课标版) 参考答案与试题解析 一、选择题:本大题共12小题,每小题5分,在每小题给同的四个选项中,只有一项是符合题目要求的. 1.(5分)(2012•新课标)已知集合A={x|x2﹣x﹣2<0},B={x|﹣1<x<1},则( ) A.A⊊B B.B⊊A C.A=B D.A∩B=∅ 2.(5分)(2012•新课标)复数z=的共轭复数是( ) A.2+i B.2﹣i C.﹣1+i D.﹣1﹣i 3.(5分)(2012•新课标)在一组样本数据(x1,y1),(x2,y2),…,(xn,yn)(n≥2,x1,x2,…,xn不全相等)的散点图中,若所有样本点(xi,yi)(i=1,2,…,n)都在直线y=x+1上,则这组样本数据的样本相关系数为( ) A.﹣1 B.0 C. D.1 4.(5分)(2012•新课标)设F1、F2是椭圆的左、右焦点,P为直线x=上一点,△F2PF1是底角为30°的等腰三角形,则E的离心率为( ) A. B. C. D. 5.(5分)(2012•新课标)已知正三角形ABC的顶点A(1,1),B(1,3),顶点C在第一象限,若点(x,y)在△ABC内部,则z=﹣x+y的取值范围是( ) A.(1﹣,2) B.(0,2) C.(﹣1,2) D.(0,1+) 6.(5分)(2012•新课标)如果执行右边的程序框图,输入正整数N(N≥2)和实数a1,a2,…,an,输出A,B,则( ) A.A+B为a1,a2,…,an的和 B.为a1,a2,…,an的算术平均数 C.A和B分别是a1,a2,…,an中最大的数和最小的数 D.A和B分别是a1,a2,…,an中最小的数和最大的数 7.(5分)(2012•新课标)如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为( ) A.6 B.9 C.12 D.18 8.(5分)(2012•新课标)平面α截球O的球面所得圆的半径为1,球心O到平面α的距离为,则此球的体积为( ) A.π B.4π C.4π D.6π 9.(5分)(2012•新课标)已知ω>0,0<φ<π,直线x=和x=是函数f(x)=sin(ωx+φ)图象的两条相邻的对称轴,则φ=( ) A. B. C. D. 10.(5分)(2012•新课标)等轴双曲线C的中心在原点,焦点在x轴上,C与抛物线y2=16x的准线交于A,B两点,,则C的实轴长为( ) A. B. C.4 D.8 11.(5分)(2012•新课标)当0<x≤时,4x<logax,则a的取值范围是( ) A.(0,) B.(,1) C.(1,) D.(,2) 12.(5分)(2012•新课标)数列{an}满足an+1+(﹣1)nan=2n﹣1,则{an}的前60项和为( ) A.3690 B.3660 C.1845 D.1830 二.填空题:本大题共4小题,每小题5分. 13.(5分)(2012•新课标)曲线y=x(3lnx+1)在点(1,1)处的切线方程为 . 14.(5分)(2012•新课标)等比数列{an}的前n项和为Sn,若S3+3S2=0,则公比q= . 15.(5分)(2012•新课标)已知向量夹角为45°,且,则= . 16.(5分)(2012•新课标)设函数f(x)=的最大值为M,最小值为m,则M+m= . 三、解答题:解答应写出文字说明,证明过程或演算步骤. 17.(12分)(2012•新课标)已知a,b,c分别为△ABC三个内角A,B,C的对边, (1)求A; (2)若a=2,△ABC的面积为,求b,c. 18.(12分)(2012•新课标)某花店每天以每枝5元的价格从农场购进若干枝玫瑰花,然后以每枝10元的价格出售.如果当天卖不完,剩下的玫瑰花做垃圾处理. (Ⅰ)若花店一天购进17枝玫瑰花,求当天的利润y(单位:元)关于当天需求量n(单位:枝,n∈N)的函数解析式. (Ⅱ)花店记录了100天玫瑰花的日需求量(单位:枝),整理得下表: 日需求量n 14 15 16 17 18 19 20 频数 10 20 16 16 15 13 10 (i)假设花店在这100天内每天购进17枝玫瑰花,求这100天的日利润(单位:元)的平均数; (ii)若花店一天购进17枝玫瑰花,以100天记录的各需求量的频率作为各需求量发生的概率,求当天的利润不少于75元的概率. 19.(12分)(2012•新课标)如图,三棱柱ABC﹣A1B1C1中,侧棱垂直底面,∠ACB=90°,AC=BC=AA1,D是棱AA1的中点. (Ⅰ)证明:平面BDC1⊥平面BDC (Ⅱ)平面BDC1分此棱柱为两部分,求这两部分体积的比. 20.(12分)(2012•新课标)设抛物线C:x2=2py(p>0)的焦点为F,准线为l,A∈C,已知以F为圆心,FA为半径的圆F交l于B,D两点; (1)若∠BFD=90°,△ABD的面积为,求p的值及圆F的方程; (2)若A,B,F三点在同一直线m上,直线n与m平行,且n与C只有一个公共点,求坐标原点到m,n距离的比值. 21.(12分)(2012•新课标)设函数f(x)=ex﹣ax﹣2. (Ⅰ)求f(x)的单调区间; (Ⅱ)若a=1,k为整数,且当x>0时,(x﹣k)f′(x)+x+1>0,求k的最大值. 22.(10分)(2012•新课标)如图,D,E分别为△ABC边AB,AC的中点,直线DE交△ABC的外接圆于F,G两点,若CF∥AB,证明: (1)CD=BC; (2)△BCD∽△GBD. 23.(2012•新课标)选修4﹣4;坐标系与参数方程 已知曲线C1的参数方程是(φ为参数),以坐标原点为极点,x轴的正半轴为极轴建立坐标系,曲线C2的坐标系方程是ρ=2,正方形ABCD的顶点都在C2上,且A,B,C,D依逆时针次序排列,点A的极坐标为(2,). (1)求点A,B,C,D的直角坐标; (2)设P为C1上任意一点,求|PA|2+|PB|2+|PC|2+|PD|2的取值范围. 24.(2012•新课标)已知函数f(x)=|x+a|+|x﹣2| (1)当a=﹣3时,求不等式f(x)≥3的解集; (2)若f(x)≤|x﹣4|的解集包含[1,2],求a的取值范围. 2012年全国统一高考数学试卷(文科)(新课标版) 参考答案与试题解析 一、选择题:本大题共12小题,每小题5分,在每小题给同的四个选项中,只有一项是符合题目要求的. 1.(5分) 【考点】集合的包含关系判断及应用.菁优网版权所有 【专题】集合. 【分析】先求出集合A,然后根据集合之间的关系可判断 【解答】解:由题意可得,A={x|﹣1<x<2}, ∵B={x|﹣1<x<1}, 在集合B中的元素都属于集合A,但是在集合A中的元素不一定在集合B中,例如x= ∴B⊊A. 故选B. 【点评】本题主要考查了集合之间关系的判断,属于基础试题. 2.(5分) 【考点】复数代数形式的乘除运算;复数的基本概念.菁优网版权所有 【专题】计算题. 【分析】利用复数的分子、分母同乘分母的共轭复数,把复数化为a+bi的形式,然后求法共轭复数即可. 【解答】解:复数z====﹣1+i. 所以复数的共轭复数为:﹣1﹣i. 故选D. 【点评】本题考查复数的代数形式的混合运算,复数的基本概念,考查计算能力. 3.(5分) 【考点】相关系数.菁优网版权所有 【专题】规律型. 【分析】所有样本点(xi,yi)(i=1,2,…,n)都在直线y=x+1上,故这组样本数据完全正相关,故其相关系数为1. 【解答】解:由题设知,所有样本点(xi,yi)(i=1,2,…,n)都在直线y=x+1上, ∴这组样本数据完全正相关,故其相关系数为1, 故选D. 【点评】本题主要考查样本的相关系数,是简单题. 4.(5分) 【考点】椭圆的简单性质.菁优网版权所有 【专题】计算题. 【分析】利用△F2PF1是底角为30°的等腰三角形,可得|PF2|=|F2F1|,根据P为直线x=上一点,可建立方程,由此可求椭圆的离心率. 【解答】解:∵△F2PF1是底角为30°的等腰三角形, ∴|PF2|=|F2F1| ∵P为直线x=上一点 ∴ ∴ 故选C. 【点评】本题考查椭圆的几何性质,解题的关键是确定几何量之间的关系,属于基础题. 5.(5分) 【考点】简单线性规划的应用.菁优网版权所有 【专题】计算题. 【分析】由A,B及△ABC为正三角形可得,可求C的坐标,然后把三角形的各顶点代入可求z的值,进而判断最大与最小值,即可求解范围 【解答】解:设C(a,b),(a>0,b>0) 由A(1,1),B(1,3),及△ABC为正三角形可得,AB=AC=BC=2 即(a﹣1)2+(b﹣1)2=(a﹣1)2+(b﹣3)2=4 ∴b=2,a=1+即C(1+,2) 则此时直线AB的方程x=1,AC的方程为y﹣1=(x﹣1),直线BC的方程为y﹣3=()(x﹣1) 当直线x﹣y+z=0经过点A(1,1)时,z=0,经过点B(1,3)z=2,经过点C(1+,2)时,z=1﹣ ∴ 故选A 【点评】考查学生线性规划的理解和认识,考查学生的数形结合思想.属于基本题型. 6.(5分) 【考点】循环结构.菁优网版权所有 【专题】算法和程序框图. 【分析】分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是求出a1,a2,…,an中最大的数和最小的数. 【解答】解:分析程序中各变量、各语句的作用, 再根据流程图所示的顺序, 可知,该程序的作用是:求出a1,a2,…,an中最大的数和最小的数 其中A为a1,a2,…,an中最大的数,B为a1,a2,…,an中最小的数 故选:C. 【点评】本题主要考查了循环结构,解题的关键是建立数学模型,根据每一步分析的结果,选择恰当的数学模型,属于中档题. 7.(5分) 【考点】由三视图求面积、体积.菁优网版权所有 【专题】计算题. 【分析】通过三视图判断几何体的特征,利用三视图的数据求出几何体的体积即可. 【解答】解:该几何体是三棱锥,底面是俯视图,三棱锥的高为3; 底面三角形斜边长为6,高为3的等腰直角三角形, 此几何体的体积为V=×6×3×3=9. 故选B. 【点评】本题考查三视图与几何体的关系,考查几何体的体积的求法,考查计算能力. 8.(5分) 【考点】球的体积和表面积.菁优网版权所有 【专题】计算题. 【分析】利用平面α截球O的球面所得圆的半径为1,球心O到平面α的距离为,求出球的半径,然后求解球的体积. 【解答】解:因为平面α截球O的球面所得圆的半径为1,球心O到平面α的距离为, 所以球的半径为:=. 所以球的体积为:=4π. 故选B. 【点评】本题考查球的体积的求法,考查空间想象能力、计算能力. 9.(5分) 【考点】由y=Asin(ωx+φ)的部分图象确定其解析式.菁优网版权所有 【专题】计算题. 【分析】通过函数的对称轴求出函数的周期,利用对称轴以及φ的范围,确定φ的值即可. 【解答】解:因为直线x=和x=是函数f(x)=sin(ωx+φ)图象的两条相邻的对称轴, 所以T==2π.所以ω=1,并且sin(+φ)与sin(+φ)分别是最大值与最小值,0<φ<π, 所以φ=. 故选A. 【点评】本题考查三角函数的解析式的求法,注意函数的最值的应用,考查计算能力. 10.(5分) 【考点】圆锥曲线的综合.菁优网版权所有 【专题】计算题;压轴题. 【分析】设等轴双曲线C:x2﹣y2=a2(a>0),y2=16x的准线l:x=﹣4,由C与抛物线y2=16x的准线交于A,B两点,,能求出C的实轴长. 【解答】解:设等轴双曲线C:x2﹣y2=a2(a>0), y2=16x的准线l:x=﹣4, ∵C与抛物线y2=16x的准线l:x=﹣4交于A,B两点, ∴A(﹣4,2),B(﹣4,﹣2), 将A点坐标代入双曲线方程得=4, ∴a=2,2a=4. 故选C. 【点评】本题考查双曲线的性质和应用,解题时要认真审题,仔细解答,注意挖掘题设中的隐含条件,合理地进行等价转化. 11.(5分) 【考点】对数函数图象与性质的综合应用.菁优网版权所有 【专题】计算题;压轴题. 【分析】由指数函数和对数函数的图象和性质,将已知不等式转化为不等式恒成立问题加以解决即可 【解答】解:∵0<x≤时,1<4x≤2 要使4x<logax,由对数函数的性质可得0<a<1, 数形结合可知只需2<logax, ∴ 即对0<x≤时恒成立 ∴ 解得<a<1 故选 B 【点评】本题主要考查了指数函数和对数函数的图象和性质,不等式恒成立问题的一般解法,属基础题 12.(5分) 【考点】数列的求和.菁优网版权所有 【专题】等差数列与等比数列. 【分析】由题意可得 a2﹣a1=1,a3+a2=3,a4﹣a3=5,a5+a4=7,a6﹣a5=9,a7+a6=11,…a50﹣a49=97,变形可得 a3+a1=2,a4+a2=8,a7+a5=2,a8+a6=24,a9+a7=2,a12+a10=40,a13+a11=2,a16+a14=56,…利用 数列的结构特征,求出{an}的前60项和. 【解答】解:由于数列{an}满足an+1+(﹣1)n an=2n﹣1,故有 a2﹣a1=1,a3+a2=3,a4﹣a3=5, a5+a4=7,a6﹣a5=9,a7+a6=11,…a50﹣a49=97. 从而可得 a3+a1=2,a4+a2=8,a7+a5=2,a8+a6=24,a11+a9=2,a12+a10=40,a15+a13=2,a16+a14=56,… 从第一项开始,依次取2个相邻奇数项的和都等于2, 从第二项开始,依次取2个相邻偶数项的和构成以8为首项,以16为公差的等差数列. {an}的前60项和为 15×2+(15×8+)=1830, 故选D. 【点评】本题主要考查数列求和的方法,等差数列的求和公式,注意利用数列的结构特征,属于中档题. 二.填空题:本大题共4小题,每小题5分. 13.(5分) 【考点】利用导数研究曲线上某点切线方程.菁优网版权所有 【专题】计算题. 【分析】先求导函数,求出切线的斜率,再求切线的方程. 【解答】解:求导函数,可得y′=3lnx+4, 当x=1时,y′=4, ∴曲线y=x(3lnx+1)在点(1,1)处的切线方程为y﹣1=4(x﹣1),即y=4x﹣3. 故答案为:y=4x﹣3. 【点评】本题考查导数的几何意义,考查点斜式求直线的方程,属于基础题. 14.(5分) 【考点】等比数列的前n项和.菁优网版权所有 【专题】计算题. 【分析】由题意可得,q≠1,由S3+3S2=0,代入等比数列的求和公式可求q 【解答】解:由题意可得,q≠1 ∵S3+3S2=0 ∴ ∴q3+3q2﹣4=0 ∴(q﹣1)(q+2)2=0 ∵q≠1 ∴q=﹣2 故答案为:﹣2 【点评】本题主要考查了等比数列的求和公式的应用,解题中要注意公比q是否为1 15.(5分) 【考点】平面向量数量积的运算;平面向量数量积的坐标表示、模、夹角.菁优网版权所有 【专题】计算题;压轴题. 【分析】由已知可得,=,代入|2|====可求 【解答】解:∵,=1 ∴= ∴|2|==== 解得 故答案为:3 【点评】本题主要考查了向量的数量积 定义的应用,向量的数量积性质||=是求解向量的模常用的方法 16.(5分) 【考点】导数在最大值、最小值问题中的应用.菁优网版权所有 【专题】综合题;压轴题. 【分析】函数可化为f(x)==,令,则为奇函数,从而函数的最大值与最小值的和为0,由此可得函数f(x)=的最大值与最小值的和. 【解答】解:函数可化为f(x)==, 令,则为奇函数, ∴的最大值与最小值的和为0. ∴函数f(x)=的最大值与最小值的和为1+1+0=2. 即M+m=2. 故答案为:2. 【点评】本题考查函数的最值,考查函数的奇偶性,解题的关键是将函数化简,转化为利用函数的奇偶性解题. 三、解答题:解答应写出文字说明,证明过程或演算步骤. 17.(12分) 【考点】解三角形.菁优网版权所有 【专题】计算题. 【分析】(1)由正弦定理及两角和的正弦公式可得sinAcosC+sinAsinC=sinB+sinC=sin(A+C)+sinC=sinAcosC+sinCcosA+sinC,整理可求A (2)由(1)所求A及S=可求bc,然后由余弦定理,a2=b2+c2﹣2bccosA=(b+c)2﹣2bc﹣2bccosA可求b+c,进而可求b,c 【解答】解:(1)∵acosC+asinC﹣b﹣c=0 ∴sinAcosC+sinAsinC﹣sinB﹣sinC=0 ∴sinAcosC+sinAsinC=sinB+sinC=sin(A+C)+sinC=sinAcosC+sinCcosA+sinC ∵sinC≠0 ∴sinA﹣cosA=1 ∴sin(A﹣30°)= ∴A﹣30°=30° ∴A=60° (2)由 由余弦定理可得,a2=b2+c2﹣2bccosA=(b+c)2﹣2bc﹣2bccosA 即4=(b+c)2﹣3bc=(b+c)2﹣12 ∴b+c=4 解得:b=c=2 【点评】本题综合考查了三角公式中的正弦定理、余弦定理、三角形的面积公式的综合应用,诱导公式与辅助角公式在三角函数化简中的应用是求解的基础,解题的关键是熟练掌握基本公式 18.(12分) 【考点】概率的应用;函数解析式的求解及常用方法;众数、中位数、平均数.菁优网版权所有 【专题】综合题;概率与统计. 【分析】(Ⅰ)根据卖出一枝可得利润5元,卖不出一枝可得赔本5元,即可建立分段函数; (Ⅱ)(i)这100天的日利润的平均数,利用100天的销售量除以100即可得到结论; (ii)当天的利润不少于75元,当且仅当日需求量不少于16枝,故可求当天的利润不少于75元的概率. 【解答】解:(Ⅰ)当日需求量n≥17时,利润y=85;当日需求量n<17时,利润y=10n﹣85;(4分) ∴利润y关于当天需求量n的函数解析式(n∈N*)(6分) (Ⅱ)(i)这100天的日利润的平均数为元;(9分) (ii)当天的利润不少于75元,当且仅当日需求量不少于16枝,故当天的利润不少于75元的概率为P=0.16+0.16+0.15+0.13+0.1=0.7.(12分) 【点评】本题考查函数解析式的确定,考查概率知识,考查利用数学知识解决实际问题,属于中档题. 19.(12分) 【考点】平面与平面垂直的判定;棱柱的结构特征;棱柱、棱锥、棱台的体积.菁优网版权所有 【专题】计算题;证明题. 【分析】(Ⅰ)由题意易证DC1⊥平面BDC,再由面面垂直的判定定理即可证得平面BDC1⊥平面BDC; (Ⅱ)设棱锥B﹣DACC1的体积为V1,AC=1,易求V1=××1×1=,三棱柱ABC﹣A1B1C1的体积V=1,于是可得(V﹣V1):V1=1:1,从而可得答案. 【解答】证明:(1)由题设知BC⊥CC1,BC⊥AC,CC1∩AC=C, ∴BC⊥平面ACC1A1,又DC1⊂平面ACC1A1, ∴DC1⊥BC. 由题设知∠A1DC1=∠ADC=45°, ∴∠CDC1=90°,即DC1⊥DC,又DC∩BC=C, ∴DC1⊥平面BDC,又DC1⊂平面BDC1, ∴平面BDC1⊥平面BDC; (2)设棱锥B﹣DACC1的体积为V1,AC=1,由题意得V1=××1×1=, 又三棱柱ABC﹣A1B1C1的体积V=1, ∴(V﹣V1):V1=1:1, ∴平面BDC1分此棱柱两部分体积的比为1:1. 【点评】本题考查平面与平面垂直的判定,着重考查线面垂直的判定定理的应用与棱柱、棱锥的体积,考查分析,表达与运算能力,属于中档题. 20.(12分) 【考点】圆锥曲线的综合;圆的标准方程;抛物线的简单性质.菁优网版权所有 【专题】综合题;压轴题. 【分析】(1)由对称性知:△BFD是等腰直角△,斜边|BD|=2p点A到准线l的距离,由△ABD的面积S△ABD=,知=,由此能求出圆F的方程. (2)由对称性设,则点A,B关于点F对称得:,得:,由此能求出坐标原点到m,n距离的比值. 【解答】解:(1)由对称性知:△BFD是等腰直角△,斜边|BD|=2p 点A到准线l的距离, ∵△ABD的面积S△ABD=, ∴=, 解得p=2,所以F坐标为(0,1), ∴圆F的方程为x2+(y﹣1)2=8. (2)由题设,则, ∵A,B,F三点在同一直线m上, 又AB为圆F的直径,故A,B关于点F对称. 由点A,B关于点F对称得: 得:,直线,切点 直线 坐标原点到m,n距离的比值为. 【点评】本题考查抛物线与直线的位置关系的综合应用,具体涉及到抛物线的简单性质、圆的性质、导数的应用,解题时要认真审题,仔细解答,注意合理地进行等价转化. 21.(12分) 【考点】利用导数求闭区间上函数的最值;利用导数研究函数的单调性.菁优网版权所有 【专题】综合题;压轴题;分类讨论;转化思想. 【分析】(Ⅰ)求函数的单调区间,可先求出函数的导数,由于函数中含有字母a,故应按a的取值范围进行分类讨论研究函数的单调性,给出单调区间; (II)由题设条件结合(I),将不等式,(x﹣k) f´(x)+x+1>0在x>0时成立转化为k<(x>0)成立,由此问题转化为求g(x)=在x>0上的最小值问题,求导,确定出函数的最小值,即可得出k的最大值; 【解答】解:(I)函数f(x)=ex﹣ax﹣2的定义域是R,f′(x)=ex﹣a, 若a≤0,则f′(x)=ex﹣a≥0,所以函数f(x)=ex﹣ax﹣2在(﹣∞,+∞)上单调递增. 若a>0,则当x∈(﹣∞,lna)时,f′(x)=ex﹣a<0; 当x∈(lna,+∞)时,f′(x)=ex﹣a>0; 所以,f(x)在(﹣∞,lna)单调递减,在(lna,+∞)上单调递增. (II)由于a=1,所以,(x﹣k) f´(x)+x+1=(x﹣k) (ex﹣1)+x+1 故当x>0时,(x﹣k) f´(x)+x+1>0等价于k<(x>0)① 令g(x)=,则g′(x)= 由(I)知,当a=1时,函数h(x)=ex﹣x﹣2在(0,+∞)上单调递增, 而h(1)<0,h(2)>0, 所以h(x)=ex﹣x﹣2在(0,+∞)上存在唯一的零点, 故g′(x)在(0,+∞)上存在唯一的零点,设此零点为α,则有α∈(1,2) 当x∈(0,α)时,g′(x)<0;当x∈(α,+∞)时,g′(x)>0; 所以g(x)在(0,+∞)上的最小值为g(α). 又由g′(α)=0,可得eα=α+2所以g(α)=α+1∈(2,3) 由于①式等价于k<g(α),故整数k的最大值为2. 【点评】本题考查利用导数求函数的最值及利用导数研究函数的单调性,解题的关键是第一小题应用分类的讨论的方法,第二小题将问题转化为求函数的最小值问题,本题考查了转化的思想,分类讨论的思想,考查计算能力及推理判断的能力,综合性强,是高考的重点题型,难度大,计算量也大,极易出错. 22.(10分) 【考点】相似三角形的判定.菁优网版权所有 【专题】证明题. 【分析】(1)根据D,E分别为△ABC边AB,AC的中点,可得DE∥BC,证明四边形ADCF是平行四边形,即可得到结论; (2)证明两组对应角相等,即可证得△BCD~△GBD. 【解答】证明:(1)∵D,E分别为△ABC边AB,AC的中点 ∴DF∥BC,AD=DB ∵AB∥CF,∴四边形BDFC是平行四边形 ∴CF∥BD,CF=BD ∴CF∥AD,CF=AD ∴四边形ADCF是平行四边形 ∴AF=CD ∵,∴BC=AF,∴CD=BC. (2)由(1)知,所以. 所以∠BGD=∠DBC. 因为GF∥BC,所以∠BDG=∠ADF=∠DBC=∠BDC. 所以△BCD~△GBD. 【点评】本题考查几何证明选讲,考查平行四边形的证明,考查三角形的相似,属于基础题. 23.(2012•新课标) 【考点】椭圆的参数方程;简单曲线的极坐标方程;点的极坐标和直角坐标的互化.菁优网版权所有 【专题】综合题;压轴题. 【分析】(1)确定点A,B,C,D的极坐标,即可得点A,B,C,D的直角坐标; (2)利用参数方程设出P的坐标,借助于三角函数,即可求得|PA|2+|PB|2+|PC|2+|PD|2的取值范围. 【解答】解:(1)点A,B,C,D的极坐标为 点A,B,C,D的直角坐标为 (2)设P(x0,y0),则为参数) t=|PA|2+|PB|2+|PC|2+|PD|2=4x2+4y2+16=32+20sin2φ ∵sin2φ∈[0,1] ∴t∈[32,52] 【点评】本题考查极坐标与直角坐标的互化,考查圆的参数方程的运用,属于中档题. 24.(2012•新课标) 【考点】绝对值不等式的解法;带绝对值的函数.菁优网版权所有 【专题】计算题;压轴题. 【分析】(1)不等式等价于,或,或,求出每个不等式组的解集, 再取并集即得所求. (2)原命题等价于﹣2﹣x≤a≤2﹣x在[1,2]上恒成立,由此求得求a的取值范围. 【解答】解:(1)当a=﹣3时,f(x)≥3 即|x﹣3|+|x﹣2|≥3,即①,或②, 或③. 解①可得x≤1,解②可得x∈∅,解③可得x≥4. 把①、②、③的解集取并集可得不等式的解集为 {x|x≤1或x≥4}. (2)原命题即f(x)≤|x﹣4|在[1,2]上恒成立,等价于|x+a|+2﹣x≤4﹣x在[1,2]上恒成立, 等价于|x+a|≤2,等价于﹣2≤x+a≤2,﹣2﹣x≤a≤2﹣x在[1,2]上恒成立. 故当 1≤x≤2时,﹣2﹣x的最大值为﹣2﹣1=﹣3,2﹣x的最小值为0, 故a的取值范围为[﹣3,0]. 【点评】本题主要考查绝对值不等式的解法,关键是去掉绝对值,化为与之等价的不等式组来解,体现了分类讨论的数学思想, 属于中档题.查看更多