华师版九年级上册数学同步课件-第23章-23平行线分线段成比例

华师版九年级上册数学同步课件-第23章-23平行线分线段成比例

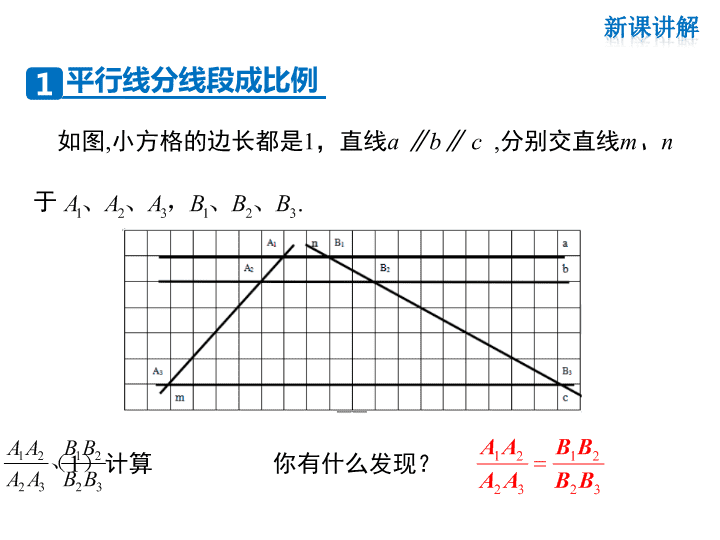
第23章 二次函数 23.1 成比例线段 23.1.2 平行线分线段成比例 问题1 ：什么是成比例线段？ 问题2： 你能不通过测量快速将一根绳子分成两部分，使 得这两部分的比是2:3？ 如图,小方格的边长都是1，直线a ∥b∥ c ,分别交直线m、n 于 （1）计算 你有什么发现？1 2 1 2 2 3 2 3 A A B B A A B B 、 1 2 3 1 2 3 .A A A B B B、 、 ， 、 、 1 2 1 2 2 3 2 3 A A B B A A B B  1 平行线分线段成比例 （2）　将直线ｂ向下平移到如下图的位置，直线m、n与直 线ｂ的交点分别为 .你在问题（１）中发现的结论还 成立吗？如果将ｂ平移到其他位置呢？ 2 2A B、 结论还成立，直线b平移到其他位置依然成立. （３）在平面上任意作三条平行线，用它们截两条直线， 截得的线段成比例吗？ 若a ∥b∥ c ，则 . 符号语言： 32 21 32 21 BB BB AA AA  成比例 两条直线被一组平行线所截，所得的对应线段成比例. （简称“平行线分线段成比例”） 归纳 1.如何理解“对应线段”？ 2.“对应线段”成比例都有哪些表达形式？ 议一议 如图1，直线a ∥b∥ c ，分别交直线m、n于 A1、A2、A3，B1、 B2、B3 .过点A1作直线n的平行线，分别交直线b、c于点C1、C2. 如图2 ，图2中有哪些成比例线段？ 图1 图2 m n m n A1 A2 A3 B1 B2 B3 A1 A2 A3 B1 B2 B3 C1 C2 a b c a b c 2 平行于三角形一边的直线的性质 ★推论： 平行于三角形一边的直线截其他两边（或两边的延长 线），所得的对应线段成比例. ★成比例线段： 1 2 1 2 2 3 2 3 A A B B A A B B ， 1 1 1 2 1 2 2 3 AC B B C C B B ， 1 2 1 1 2 3 1 2 A A AC A A C C 等. 如图，在△ABC中， EF∥BC. （1）如果E、F分别是AB和AC上的点， AE = BE=7, FC = 4 ， 那么 AF的长是多少？ （2）如果AB = 10, AE=6，AF = 5 ，那么FC的长是多少？ A B C E F   71 7 4 4        AE AF AFEF BC , ,BE FC AF . 解 ，： ∥   6 52 10 25 25 1053 3 3            AE AF ,AB AC AC AC FC AC AF .， 例题 思考：当平行线之间的距离相等时，对应线段的比是多少？ DE=EF, MN=ON. 对应线段的比是1. 2.如图，在△ABC中，D、E分别是AB和AC上的点，且 DE∥BC. （1）如果AD = 3.2cm, DB = 1.2cm ，AE=2.4cm,那么EC的长是 多少？ （2）如果AB = 5cm, AD=3cm，AC = 4cm ，那么EC的长是多少？ A B C D E   3 2 2 41 1 2 0 9        AD AE . .DE BC ,BD EC . EC EC . . 解: ∥ ，   32 5 4 2 4 4 2 4 1 6             AD AE AEDE BC ,AB AC AE . ,EC AC AE . . . ∥ ， 1.两条直线被一组平行线所截，所得的对应线段成比例； 2.平行于三角形一边的直线截其他两边（或两边的延长 线)，所得的对应线段成比例.