- 2021-05-10 发布 |
- 37.5 KB |
- 19页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2018中考数学专题复习压轴题集训含答案
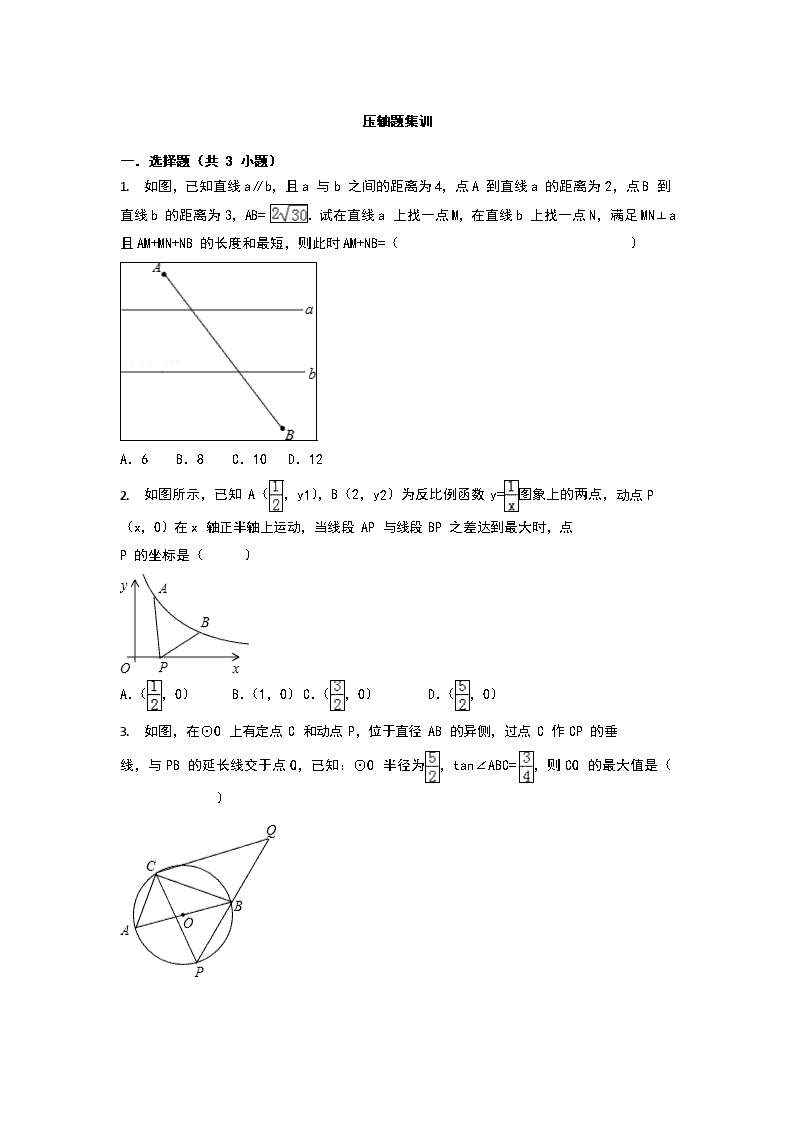
压轴题集训 一.选择题(共 3 小题) 1. 如图,已知直线 a∥b,且 a 与 b 之间的距离为 4,点 A 到直线 a 的距离为 2,点 B 到直线 b 的距离为 3,AB= .试在直线 a 上找一点 M,在直线 b 上找一点 N,满足 MN⊥a 且 AM+MN+NB 的长度和最短,则此时 AM+NB=( ) A.6 B.8 C.10 D.12 2. 如图所示,已知 A(,y1),B(2,y2)为反比例函数 y=图象上的两点,动点 P(x,0)在 x 轴正半轴上运动,当线段 AP 与线段 BP 之差达到最大时,点 P 的坐标是( ) A.(,0) B.(1,0) C.(,0) D.(,0) 3. 如图,在⊙O 上有定点 C 和动点 P,位于直径 AB 的异侧,过点 C 作 CP 的垂 线,与 PB 的延长线交于点 Q,已知:⊙O 半径为,tan∠ABC= ,则 CQ 的最大值是( ) A.5 B. C. D. 二.填空题(共 11 小题) 1. 如图,△ABC 中,∠BAC=60°,∠ABC=45°,AB=2,D 是线段 BC 上的一个动点,以 AD 为直径画⊙O 分别交 AB,AC 于 E,F,连接 EF,则线段 EF 长度的最小值为 . 2. 如图,直线 y=﹣与 x 轴、y 轴分别交于点 A、B;点 Q 是以 C(0,﹣1) 为圆心、1 为半径的圆上一动点,过 Q 点的切线交线段 AB 于点 P,则线段 PQ 的最小值是 . 3. 如图,MN 为⊙O 的直径,A、B 是⊙O 上的两点,过 A 作 AC⊥MN 于点 C, 过 B 作 BD⊥MN 于点 D,P 为 DC 上的任意一点,若 MN=20,AC=8,BD=6,则 PA+PB 的最小值是 . 4. 如图,已知正方形ABCD 边长为 3,点 E 在 AB 边上且 BE=1,点 P,Q 分别是边 BC,CD 的动点(均不与顶点重合),当四边形 AEPQ 的周长取最小值时,四边 形 AEPQ 的面积是 . 1. 如图,∠AOB=30°,点 M、N 分别在边 OA、OB 上,且 OM=1,ON=3,点 P、 Q 分别在边 OB、OA 上,则 MP+PQ+QN 的最小值是 . 2. 如图,菱形 ABCD 中,∠A=60°,AB=3,⊙A、⊙B 的半径分别为 2 和 1,P、E、 F 分别是边 CD、⊙A 和⊙B 上的动点,则 PE+PF 的最小值是 . 3. 如图,在边长为 2 的菱形 ABCD 中,∠A=60°,M 是 AD 边的中点,N 是 AB 边上的一动点,将△AMN 沿 MN 所在直线翻折得到△A′MN,连接 A′C,则 A′C 长度的最小值是 . 4. 如图,在△ABC 中,∠ACB=90°,AB=5,BC=3,P 是 AB 边上的动点(不与点 B 重合),将△BCP 沿 CP 所在的直线翻折,得到△B′CP,连接 B′A,则 B′A 长度的最小值是 . 1. 如图,当四边形 PABN 的周长最小时,a= . 2. 如图,直线 l 与半径为 4 的⊙O 相切于点 A,P 是⊙O 上的一个动点(不与点 A 重合),过点 P 作 PB⊥l,垂足为 B,连接 PA.设 PA=x,PB=y,则(x﹣y)的最大值是 . 3. 如图,AB 是⊙O 的一条弦,点 C 是⊙O 上一动点,且∠ACB=30°,点 E、F 分别是 AC、BC 的中点,直线 EF 与⊙O 交于 G、H 两点.若⊙O 的半径为 7,则 GE+FH 的最大值为 . 三.解答题(共 1 小题) 4. 如图,在 Rt△ABC 中,∠ACB=90°,AC=BC=2,以 BC 为直径的半圆交 AB 于 D,P 是上的一个动点,连接 AP,求 AP 的最小值. 压轴题集训 参考答案与试题解析 一.选择题(共 3 小题) 1. 如图,已知直线 a∥b,且 a 与 b 之间的距离为 4,点 A 到直线 a 的距离为 2,点 B 到直线 b 的距离为 3,AB= .试在直线 a 上找一点 M,在直线 b 上找一点 N,满足 MN⊥a 且 AM+MN+NB 的长度和最短,则此时 AM+NB=( ) A.6 B.8 C.10 D.12 【解答】解:过 A 作直线 a 的垂线,并在此垂线上取点 A′,使得 AA′=4,连接 A′B, 与直线 b 交于点 N,过N 作直线 a 的垂线,交直线 a 于点 M,连接 AM,过点 B 作 BE⊥AA′,交射线 AA′于点 E,如图. ∵AA′⊥a,MN⊥a, ∴AA′∥MN. 又∵AA′=MN=4, ∴四边形 AA′NM 是平行四边形, ∴AM=A′N. 由于 AM+MN+NB 要最小,且 MN 固定为 4,所以 AM+NB 最小. 由两点之间线段最短,可知 AM+NB 的最小值为 A′B. ∵AE=2+3+4=9,AB= , ∴BE= =, ∵A′E=AE﹣AA′=9﹣4=5, ∴A′B= =8 所以 AM+NB 的最小值为 8. 故选:B. 1. 如图所示,已知 A(,y1),B(2,y2)为反比例函数 y=图象上的两点,动点 P(x,0)在 x 轴正半轴上运动,当线段 AP 与线段 BP 之差达到最大时,点 P 的坐标是( ) A.(,0) B.(1,0) C.(,0) D.(,0) 【解答】解:∵把 A(,y1),B(2,y2)代入反比例函数 y=得:y1=2,y2=, ∴A(,2),B(2,), ∵在△ABP 中,由三角形的三边关系定理得:|AP﹣BP|<AB, ∴延长 AB 交 x 轴于 P′,当 P 在 P′点时,PA﹣PB=AB, 即此时线段 AP 与线段 BP 之差达到最大, 设直线 AB 的解析式是 y=kx+b, 把 A、B 的坐标代入得: , 解得:k=﹣1,b= , ∴直线 AB 的解析式是 y=﹣x+ , 当 y=0 时,x=, 即 P(,0), 故选:D. 1. 如图,在⊙O 上有定点 C 和动点 P,位于直径 AB 的异侧,过点 C 作 CP 的垂线,与 PB 的延长线交于点 Q,已知:⊙O 半径为,tan∠ABC= ,则 CQ 的最 大值是( ) A.5 B. C. D. 【解答】解:∵AB 为⊙O 的直径, ∴AB=5,∠ACB=90°, ∵tan∠ABC= , ∴=, ∵CP⊥CQ, ∴∠PCQ=90°, 而∠A=∠P, ∴△ACB∽△PCQ, ∴=, ∴CQ= •PC= PC, 当 PC 最大时,CQ 最大,即 PC 为⊙O 的直径时,CQ 最大,此时 CQ=×5= . 故选:D. 二.填空题(共 11 小题) 1. 如图,△ABC 中,∠BAC=60°,∠ABC=45°,AB=2,D 是线段 BC 上的一个动点,以 AD 为直径画⊙O 分别交 AB,AC 于 E,F,连接 EF,则线段 EF 长度的最 小 值 为 . 【解答】解:由垂线段的性质可知,当 AD 为△ABC 的边 BC 上的高时,直径 AD 最短, 如图,连接 OE,OF,过 O 点作 OH⊥EF,垂足为 H, ∵在 Rt△ADB 中,∠ABC=45°,AB=2, ∴AD=BD=2,即此时圆的直径为 2, 由圆周角定理可知∠EOH=∠EOF=∠BAC=60°, ∴在 Rt△EOH 中,EH=OE•sin∠EOH=1×=, 由垂径定理可知 EF=2EH=. 故答案为:. 2. 如图,直线 y=﹣ 与 x 轴、y 轴分别交于点 A、B;点 Q 是以 C(0,﹣1) 为圆心、1 为半径的圆上一动点,过 Q 点的切线交线段 AB 于点 P,则线段 PQ 的最小值是 . 【解答】解:过点 C 作 CP⊥直线 AB 于点 P,过点 P 作⊙C 的切线 PQ,切点为 Q, 此时 PQ 最小,连接 CQ,如图所示. 当 x=0 时,y=3, ∴点 B 的坐标为(0,3);当 y=0 时,x=4, ∴点 A 的坐标为(4,0). ∴OA=4,OB=3, ∴AB= =5, ∴sinB= =. ∵C(0,﹣1), ∴BC=3﹣(﹣1)=4, ∴CP=BC•sinB= . ∵PQ 为⊙C 的切线, ∴在 Rt△CQP 中,CQ=1,∠CQP=90°, ∴PQ= =. 故答案为: . 1. 如图,MN 为⊙O 的直径,A、B 是⊙O 上的两点,过 A 作 AC⊥MN 于点 C, 过 B 作 BD⊥MN 于点 D,P 为 DC 上的任意一点,若 MN=20,AC=8,BD=6,则 PA+PB 的最小值是 14 . 【解答】解:∵MN=20, ∴⊙O 的半径=10, 连接 OA、OB, 在 Rt△OBD 中,OB=10,BD=6, ∴OD= ==8; 同理,在 Rt△AOC 中,OA=10,AC=8, ∴OC= ==6, ∴CD=8+6=14, 作点 B 关于 MN 的对称点 B′,连接 AB′,则 AB′即为 PA+PB 的最小值,B′D=BD=6, 过点 B′作 AC 的垂线,交 AC 的延长线于点 E, 在 Rt△AB′E 中, ∵AE=AC+CE=8+6=14,B′E=CD=14, ∴AB′= ==14 . 故答案为:14. 1. 如图,已知正方形ABCD 边长为 3,点 E 在 AB 边上且 BE=1,点 P,Q 分别是边 BC,CD 的动点(均不与顶点重合),当四边形 AEPQ 的周长取最小值时,四边形 AEPQ 的 面 积 是 . 【解答】解:如图 1 所示: 作 E 关于 BC 的对称点 E′,点 A 关于 DC 的对称点 A′,连接 A′E′,四边形 AEPQ 的周长最小, ∵AD=A′D=3,BE=BE′=1, ∴AA′=6,AE′=4. ∵DQ∥AE′,D 是 AA′的中点, ∴DQ 是△AA′E′的中位线, ∴DQ= AE′=2;CQ=DC﹣CQ=3﹣2=1, ∵BP∥AA′, ∴△BE′P∽△AE′A′, ∴=,即=,BP= ,CP=BC﹣BP=3﹣ =, S 四边形 AEPQ=S 正方形 ABCD﹣S△ADQ﹣S△PCQ﹣SBEP =9﹣ AD•DQ﹣ CQ•CP﹣ BE•BP =9﹣ ×3×2﹣ ×1×﹣×1× =. 故答案为:. 1. 如图,∠AOB=30°,点 M、N 分别在边 OA、OB 上,且 OM=1,ON=3,点 P、 Q 分别在边 OB、OA 上,则 MP+PQ+QN 的最小值是 . 【解答】解:作 M 关于 OB 的对称点 M′,作 N 关于 OA 的对称点 N′, 连接 M′N′,即为 MP+PQ+QN 的最小值. 根据轴对称的定义可知:∠N′OQ=∠M′OB=30°,∠ONN′=60°, ∴△ONN′为等边三角形,△OMM′为等边三角形, ∴∠N′OM′=90°, ∴在 Rt△M′ON′中, M′N′= =. 故答案为 . 1. 如图,菱形 ABCD 中,∠A=60°,AB=3,⊙A、⊙B 的半径分别为 2 和 1,P、E、 F 分别是边 CD、⊙A 和⊙B 上的动点,则 PE+PF 的最小值是 3 . 【解答】解:作 A 点关于直线 DC 的对称点 A′,连接 BD,DA′, 可得 A′A⊥DC,则∠BAA′=90°,故∠A′=30°, 则∠ABA′=60°,∠ADN=∠A′DN=60°, ∵AB=AD,∠BAD=60°, ∴△ABD 是等边三角形, ∴∠ADB=60°, ∴∠ADB+∠ADA′=180°, ∴A′,D,B 在一条直线上, 由题意可得出:此时 P 与 D 重合,E 点在 AD 上,F 在 BD 上,此时 PE+PF 最小, ∵菱形 ABCD 中,∠A=60°, ∴AB=AD,则△ABD 是等边三角形, ∴BD=AB=AD=3, ∵⊙A、⊙B 的半径分别为 2 和 1, ∴PE=1,DF=2, ∴PE+PF 的最小值是 3. 故答案为:3. 1. 如图,在边长为 2 的菱形 ABCD 中,∠A=60°,M 是 AD 边的中点,N 是 AB 边上的一动点,将△AMN 沿 MN 所在直线翻折得到△A′MN,连接 A′C,则 A′C 长度的最小值是 ﹣1 . 【解答】解:如图所示:∵MA′是定值,A′C 长度取最小值时,即 A′在 MC 上时, 过点 M 作 MF⊥DC 于点 F, ∵在边长为 2 的菱形 ABCD 中,∠A=60°,M 为 AD 中点, ∴2MD=AD=CD=2,∠FDM=60°, ∴∠FMD=30°, ∴FD= MD= , ∴FM=DM×cos30°= , ∴MC= =, ∴A′C=MC﹣MA′= ﹣1. 故答案为:﹣1. 2. 如图,在△ABC 中,∠ACB=90°,AB=5,BC=3,P 是 AB 边上的动点(不与点 B 重合),将△BCP 沿 CP 所在的直线翻折,得到△B′CP,连接 B′A,则 B′A 长度的最小值是 1 . 【解答】解:在 Rt△ABC 中,由勾股定理可知:AC===4, 由轴对称的性质可知:BC=CB′=3, 当 A、B′、C 三点在一条直线上时,B′A 有最小值, ∴B′Amin=AC﹣B′C=4﹣3=1. 故答案为:1. 1. 如图,当四边形 PABN 的周长最小时,a= . 【解答】解:将 N 点向左平移 2 单位与 P 重合,点 B 向左平移 2 单位到 B′(2, ﹣1), 作 B′关于 x 轴的对称点 B″,根据作法知点 B″(2,1),设直线 AB″的解析式为 y=kx+b, 则,解得 k=4,b=﹣7. ∴y=4x﹣7.当 y=0 时,x=,即 P(,0),a=.故答案填: . 1. 如图,直线 l 与半径为 4 的⊙O 相切于点 A,P 是⊙O 上的一个动点(不与点 A 重合),过点 P 作 PB⊥l,垂足为 B,连接 PA.设 PA=x,PB=y,则(x﹣y)的最大值是 2 . 【解答】解:如图,作直径 AC,连接 CP, ∴∠CPA=90°, ∵AB 是切线, ∴CA⊥AB, ∵PB⊥l, ∴AC∥PB, ∴∠CAP=∠APB, ∴△APC∽△PBA, ∴ , ∵PA=x,PB=y,半径为 4, ∴=, ∴y= x2, ∴x﹣y=x﹣ x2=﹣ x2+x=﹣ (x﹣4)2+2, 当 x=4 时,x﹣y 有最大值是 2, 故答案为:2. 1. 如图,AB 是⊙O 的一条弦,点 C 是⊙O 上一动点,且∠ACB=30°,点 E、F 分别是 AC、BC 的中点,直线 EF 与⊙O 交于 G、H 两点.若⊙O 的半径为 7,则 GE+FH 的最大值为 10.5 . 【解答】解:当 GH 为⊙O 的直径时,GE+FH 有最大值. 当 GH 为直径时,E 点与 O 点重合, ∴AC 也是直径,AC=14. ∵∠ABC 是直径上的圆周角, ∴∠ABC=90°, ∵∠C=30°, ∴AB= AC=7. ∵点 E、F 分别为 AC、BC 的中点, ∴EF= AB=3.5, ∴GE+FH=GH﹣EF=14﹣3.5=10.5. 故答案为:10.5. 三.解答题(共 1 小题) 2. 如图,在 Rt△ABC 中,∠ACB=90°,AC=BC=2,以 BC 为直径的半圆交 AB 于 D,P 是上的一个动点,连接 AP,求 AP 的最小值. 【解答】解:找到 BC 的中点 E,连接 AE,交半圆于 P2,在半圆上取 P1,连接AP1,EP1, 可 见 ,AP1+EP1>AE, 即 AP2 是 AP 的最小值, ∵AE= =,P2E=1, ∴AP2= ﹣1.查看更多