2006年安徽省高考数学试卷（理科）【附答案、word版本，可再编辑；B4纸型两栏】

2006年安徽省高考数学试卷（理科）【附答案、word版本，可再编辑；B4纸型两栏】

‎2006年安徽省高考数学试卷（理科）‎ 一、选择题（共12小题，每小题5分，满分60分）‎ ‎1. 复数‎1+‎3‎i‎3‎‎-i等于（ ）‎ A.i B.‎-i C.‎3‎‎+i D.‎‎3‎‎-i ‎2. 设集合A={x||x-2|≤2, x∈R}‎，B={y|y=-x‎2‎, -1≤x≤2}‎，则‎∁‎R‎(A∩B)‎等于（ ）‎ A.R B.‎{x|x∈R, x≠0}‎ C.‎{0}‎ D.‎‎⌀‎ ‎3. 若抛物线y‎2‎‎=2px的焦点与椭圆x‎2‎‎6‎‎+y‎2‎‎2‎=1‎的右焦点重合，则p的值为‎(‎         ‎‎)‎ A.‎-2‎ B.‎2‎ C.‎-4‎ D.‎‎4‎ ‎4. 设a，b∈R，已知命题p:a=b；命题q：‎(a+b‎2‎‎)‎‎2‎≤‎a‎2‎‎+‎b‎2‎‎2‎，则p是q成立的（ ）‎ A.必要不充分条件 B.充分不必要条件 C.充分必要条件 D.既不充分也不必要条件 ‎5. 函数y=‎‎2x,x≥0‎‎-x‎2‎，x<0‎的反函数是（ ）‎ A.y=‎x‎2‎‎，x≥0‎‎-x‎，x<0‎ B.‎y=‎‎2x,x≥0‎‎-x‎，x<0‎ C.y=‎x‎2‎‎，x≥0‎‎-‎-x，x<0‎ D.‎y=‎‎2x,x≥0‎‎-‎-x，x<0‎ ‎6. 将函数y=sinωx(ω>0)‎的图象按向量a‎→‎‎=(-π‎6‎,0)‎平移，平移后的图象如图所示，则平移后的图象所对应函数的解析式是（ ）‎ A.y=sin(x+π‎6‎)‎ B.y=sin(x-π‎6‎)‎ C.y=sin(2x+π‎3‎)‎ D.‎y=sin(2x-π‎3‎)‎ ‎7. 若曲线y=‎x‎4‎的一条切线l与直线x+4y-8=0‎垂直，则l的方程为（ ）‎ A.‎4x-y-3=0‎ B.x+4y-5=0‎ C.‎4x-y+3=0‎ D.‎x+4y+3=0‎ ‎8. 设‎00‎，‎(ax‎2‎+‎‎1‎x‎)‎‎4‎展开式中x‎3‎的系数为‎3‎‎2‎，则limn→∞‎‎(a+a‎2‎+…+an)=‎________．‎ ‎14. 在‎▱ABCD中，AB‎→‎‎=‎a‎→‎，AD‎→‎‎=‎b‎→‎，AN‎→‎‎=3‎NC‎→‎，M为BC的中点，则MN‎→‎‎=‎________（用a，b表示）．‎ ‎15. 函数f(x)‎对于任意实数x满足条件f(x+2)=‎‎1‎f(x)‎，若f(1)‎＝‎-5‎，则f[f(5)]‎＝________．‎ ‎16. 多面体上，位于同一条棱两端的顶点称为相邻的，如图，正方体的一个顶点A在平面α内，其余顶点在α的同侧，正方体上与顶点A相邻的三个顶点到α的距离分别为‎1‎，‎2‎和‎4‎，P是正方体的其余四个顶点中的一个，则P到平面α的距离可能是：①‎3‎；②‎4‎； ③‎5‎；④‎6‎；⑤‎7‎．以上结论正确的为________．（写出所有正确结论的编号）‎ 三、解答题（共6小题，满分74分）‎ ‎17. 已知‎3π‎4‎‎<α<π，tanα+cotα=-‎‎10‎‎3‎ ‎ ‎（1）求tanα的值；‎ ‎（2）求‎5sin‎2‎α‎2‎+8sinα‎2‎cosα‎2‎+11cos‎2‎α‎2‎-8‎‎2‎sin(α-π‎2‎)‎的值．‎ ‎18. 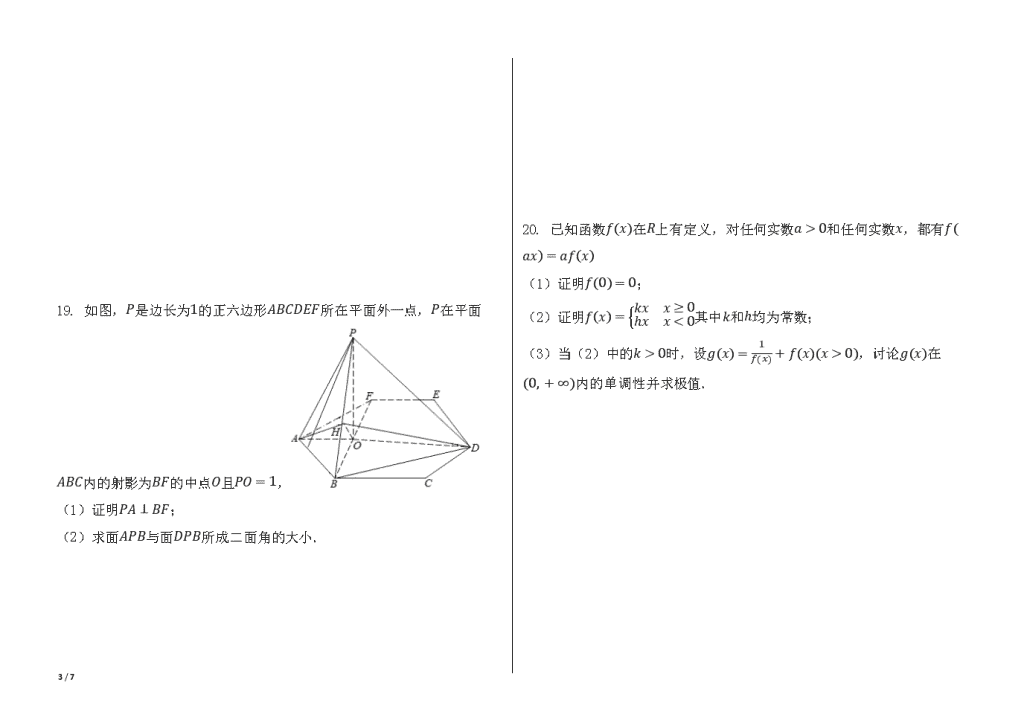在添加剂的搭配使用中，为了找到最佳的搭配方案，需要对各种不同的搭配方式作比较．在试制某种牙膏新品种时，需要选用两种不同的添加剂．现有芳香度分别为‎0‎，‎1‎，‎2‎，‎3‎，‎4‎，‎5‎的六种添加剂可供选用．根据试验设计原理，通常首先要随机选取两种不同的添加剂进行搭配试验．用 ‎ 7 / 7‎ ξ表示所选用的两种不同的添加剂的芳香度之和． ‎ ‎（1）写出ξ的分布列；（以列表的形式给出结论，不必写计算过程）‎ ‎（2）求ξ的数学期望Eξ．（要求写出计算过程或说明道理）‎ ‎19. 如图，P是边长为‎1‎的正六边形ABCDEF所在平面外一点，P在平面ABC内的射影为BF的中点O且PO=1‎， ‎ ‎（1）证明PA⊥BF；‎ ‎（2）求面APB与面DPB所成二面角的大小．‎ ‎20. 已知函数f(x)‎在R上有定义，对任何实数a>0‎和任何实数x，都有f(ax)=af(x)‎ ‎ ‎（1）证明f(0)=0‎；‎ ‎（2）证明f(x)=‎kxx≥0‎hxx<0‎其中k和h均为常数；‎ ‎（3）当（2）中的k>0‎时，设g(x)=‎1‎f(x)‎+f(x)(x>0)‎，讨论g(x)‎在‎(0, +∞)‎内的单调性并求极值．‎ ‎ 7 / 7‎ ‎21. 数列‎{an}‎的前n项和为Sn，已知a‎1‎‎=‎1‎‎2‎，Sn=n‎2‎an-n(n-1)‎，n=1‎，‎2‎，…写出Sn与Sn-1‎的递推关系式‎(n≥2)‎，并求Sn关于n的表达式．‎ ‎22. 如图，F为双曲线C:x‎2‎a‎2‎-y‎2‎b‎2‎=1(a>0, b>0)‎的右焦点．P为双曲线C右支上一点，且位于x轴上方，M为左准线上一点，O为坐标原点．已知四边形OFPM为平行四边形，‎|PF|=λ|OF|‎． ‎ ‎（1）写出双曲线C的离心率e与λ的关系式；‎ ‎（2）当λ=1‎时，经过焦点F且平行于OP的直线交双曲线于A、B点，若‎|AB|=12‎，求此时的双曲线方程．‎ ‎ 7 / 7‎ 参考答案与试题解析 ‎2006年安徽省高考数学试卷（理科）‎ 一、选择题（共12小题，每小题5分，满分60分）‎ ‎1.A ‎2.B ‎3.D ‎4.B ‎5.C ‎6.C ‎7.A ‎8.B ‎9.A ‎10.B ‎11.D ‎12.C 二、填空题（共4小题，每小题4分，满分16分）‎ ‎13.‎‎1‎ ‎14.‎‎-‎1‎‎4‎a‎→‎+‎‎1‎‎4‎b‎→‎ ‎15.‎‎-‎‎1‎‎5‎ ‎16.①③④⑤‎ 三、解答题（共6小题，满分74分）‎ ‎17.解：（1）由tanα+cotα=-‎‎10‎‎3‎得‎3tan‎2‎α+10tanα+3=0‎，‎ 即tanα=-3‎或tanα=-‎‎1‎‎3‎，又‎3π‎4‎‎<α<π，‎ 所以tanα=-‎‎1‎‎3‎为所求．‎ ‎（2）‎‎5sin‎2‎α‎2‎+8sinα‎2‎cosα‎2‎+11cos‎2‎α‎2‎-8‎‎2‎sin(α-π‎2‎)‎ ‎=‎‎5‎1-cosα‎2‎+4sinα+11‎1+cosα‎2‎-8‎‎-‎2‎cosα ‎=‎‎5-5cosα+8sinα+11+11cosα-16‎‎-2‎2‎cosα ‎=‎8sinα+6cosα‎-2‎2‎cosα=‎‎8tanα+6‎‎-2‎‎2‎ ‎=-‎‎5‎‎2‎‎6‎‎．‎ ‎18.解：（1）‎ ‎（2）由前一问的分布列可知每一个变量和变量所对应的概率，用期望的公式写出期望的表达式，计算出结果 Eξ=1×‎1‎‎15‎+2×‎1‎‎15‎+3×‎2‎‎15‎+4×‎2‎‎15‎+5×‎3‎‎15‎+6×‎2‎‎15‎+7×‎2‎‎15‎+8×‎2‎‎15‎+9×‎1‎‎15‎=5‎ ‎19.解：（1）在正六边形ABCDEF中，‎△ABF为等腰三角形，‎ ‎∵ P在平面ABC内的射影为O，‎ ‎ 7 / 7‎ ‎∴ PO⊥‎平面ABF，‎ ‎∴ AO为PA在平面ABF内的射影；‎ ‎∵ O为BF中点，∴ AO⊥BF，‎ ‎∴ PA⊥BF．‎ ‎（2）解法一：‎ ‎∵ PO⊥‎平面ABF，‎ ‎∴ 平面PBF⊥‎平面ABC；而O为BF中点，ABCDEF是正六边形，‎ ‎∴ A、O、D共线，且直线AD⊥BF，则AD⊥‎平面PBF；‎ 又∵ 正六边形ABCDEF的边长为‎1‎，‎ ‎∴ AO=‎‎1‎‎2‎，DO=‎‎3‎‎2‎，BO=‎‎3‎‎2‎．‎ 过O在平面POB内作OH⊥PB于H，连AH、DH，则AH⊥PB，DH⊥PB，‎ 所以‎∠AHD为所求二面角平面角．‎ 在‎△AHO中，OH=‎‎21‎‎7‎，tan∠AHO=AOOH=‎1‎‎2‎‎21‎‎7‎=‎‎7‎‎2‎‎21‎．‎ 在‎△DHO中，tan∠DHO=DOOH=‎3‎‎2‎‎21‎‎7‎=‎‎21‎‎2‎；‎ 而tan∠AHD=tan(∠AHO+∠DHO)=‎7‎‎2‎‎21‎‎+‎‎21‎‎2‎‎1-‎7‎‎2‎‎21‎×‎‎21‎‎2‎=-‎4×28‎‎3‎‎21‎=‎‎16‎‎21‎‎9‎ ‎（2）解法二：‎ 以O为坐标原点，建立空间直角坐标系，P(0, 0, 1)‎，A(0, -‎1‎‎2‎, 0)‎，B(‎3‎‎2‎, 0, 0)‎，D(0, 2, 0)‎，‎ ‎∴ PA‎→‎‎=(0,-‎1‎‎2‎,-1)‎，PB‎→‎‎=(‎3‎‎2‎,0,-1)‎，‎PD‎→‎‎=(0,2,-1)‎ 设平面PAB的法向量为n‎1‎‎→‎‎=(x‎1‎,y‎1‎,1)‎，则n‎1‎‎→‎‎⊥‎PA‎→‎，n‎1‎‎→‎‎⊥‎PB‎→‎，‎ 得‎-‎1‎‎2‎y‎1‎-1=0‎‎3‎‎2‎x‎1‎‎-1=0‎，n‎1‎‎→‎‎=(‎2‎‎3‎‎3‎,-2,1)‎；‎ 设平面PDB的法向量为n‎2‎‎→‎‎=(x‎2‎,y‎2‎,1)‎，则n‎2‎‎→‎‎⊥‎PD‎→‎，n‎2‎‎→‎‎⊥‎PB‎→‎，‎ 得‎2y‎2‎-1=0‎‎3‎‎2‎x‎2‎‎-1=0‎，n‎2‎‎→‎‎=(‎2‎‎3‎‎3‎,‎1‎‎2‎,1)‎；‎ cos=‎|n‎1‎‎→‎|⋅|n‎2‎‎→‎|‎‎˙‎=‎‎8‎‎589‎‎589‎ ‎20.证明（1）令x=0‎，则f(0)=af(0)‎，‎ ‎∵ a>0‎，‎ ‎∴ f(0)=0‎．‎ ‎（2）①令x=a，‎ ‎∵ a>0‎，‎ ‎∴ x>0‎，则f(x‎2‎)=xf(x)‎．‎ 假设x≥0‎时，f(x)=kx(k∈R)‎，则f(x‎2‎)=kx‎2‎，而xf(x)=x⋅kx=kx‎2‎，‎ ‎∴ f(x‎2‎)=xf(x)‎，即f(x)=kx成立．‎ ‎②令x=-a，‎ ‎∵ a>0‎，‎ ‎∴ x<0‎，‎f(-x‎2‎)=-xf(x)‎ 假设x<0‎时，f(x)=hx(h∈R)‎，则f(-x‎2‎)=-hx‎2‎，而‎-xf(x)=-x⋅hx=-hx‎2‎，‎ ‎ 7 / 7‎ ‎∴ f(-x‎2‎)=-xf(x)‎，即f(x)=hx成立．‎ ‎∴ f(x)=‎kx,x≥0‎hx,x<0‎成立．‎ ‎（3）当x>0‎时，g(x)=‎1‎f(x)‎+f(x)=‎1‎kx+kx，‎g'(x)=-‎1‎kx‎2‎+k=‎k‎2‎x‎2‎‎-1‎kx‎2‎ 令g‎'‎‎(x)=0‎，得x=‎‎1‎k或x=-‎‎1‎k；‎ 当x∈(0, ‎1‎k)‎时，g‎'‎‎(x)<0‎，∴ g(x)‎是单调递减函数；‎ 当x∈[‎1‎k, +∞)‎时，g‎'‎‎(x)>0‎，∴ g(x)‎是单调递增函数；‎ 所以当x=‎‎1‎k时，函数g(x)‎在‎(0, +∞)‎内取得极小值，极小值为g(‎1‎k)=2‎ ‎21.解：由Sn‎=n‎2‎an-n(n-1)(n≥2)‎，‎ 得：Sn‎=n‎2‎(Sn-Sn-1‎)-n(n-1)‎，即‎(n‎2‎-1)Sn-n‎2‎Sn-1‎=n(n-1)‎，‎ 所以n+1‎nSn‎-nn-1‎Sn-1‎=1‎，对n≥2‎成立．‎ 由n+1‎nSn‎-nn-1‎Sn-1‎=1‎，nn-1‎Sn-1‎‎-n-1‎n-2‎Sn-2‎=1‎，‎3‎‎2‎S‎2‎‎-‎2‎‎1‎S‎1‎=1‎，‎ 相加得：n+1‎nSn‎-2S‎1‎=n-1‎，又S‎1‎‎=a‎1‎=‎‎1‎‎2‎，‎ 所以Sn‎=‎n‎2‎n+1‎，‎ 当n=1‎时，也成立．‎ ‎22.解：（1）∵ 四边形OFPM是平行四边形，‎ ‎∴ ‎|OF|=|PM|=c，作双曲线的右准线交PM于H，则‎|PM|=|PH|+2×‎a‎2‎c，‎ 又e=‎|PF|‎‎|PH|‎=λ|OF|‎c-2‎a‎2‎c=λcc-2‎a‎2‎c=λc‎2‎c‎2‎‎-2‎a‎2‎=‎λe‎2‎e‎2‎‎-2‎，e‎2‎‎-λe-2=0‎．‎ ‎（2）当λ=1‎时，e=2‎，‎|PF|=|OF|‎．‎ ‎∴ c=2a，b‎2‎‎=3‎a‎2‎，双曲线为x‎2‎a‎2‎‎-y‎2‎‎3‎a‎2‎=1‎且平行四边形OFPM是菱形，‎ 由图象，作PD⊥X轴于D，则直线OP的斜率为PDOD‎=C‎2‎‎-‎a‎4‎C‎2‎c-‎a‎2‎c=‎‎15‎‎3‎，则直线AB的方程为y=‎15‎‎3‎(x-2a)‎，代入到双曲线方程得：‎ ‎4x‎2‎+20ax-29a‎2‎=0‎‎，又‎|AB|=12‎，‎ 由‎|AB|=‎‎1+‎k‎2‎‎(x‎1‎+x‎2‎‎)‎‎2‎-4‎x‎1‎x‎2‎，‎ 得：‎12=‎‎8‎‎3‎‎(5a‎)‎‎2‎+4×‎‎29‎a‎2‎‎4‎，‎ 解得a=1‎，‎ 则b‎2‎‎=3‎，‎ 所以x‎2‎‎-y‎2‎‎3‎=1‎为所求．‎ ‎ 7 / 7‎