- 2021-05-07 发布 |
- 37.5 KB |
- 1页
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高中数学必修3教案:7_备课资料(2_3_2 两个变量的线性相关 第2课时)
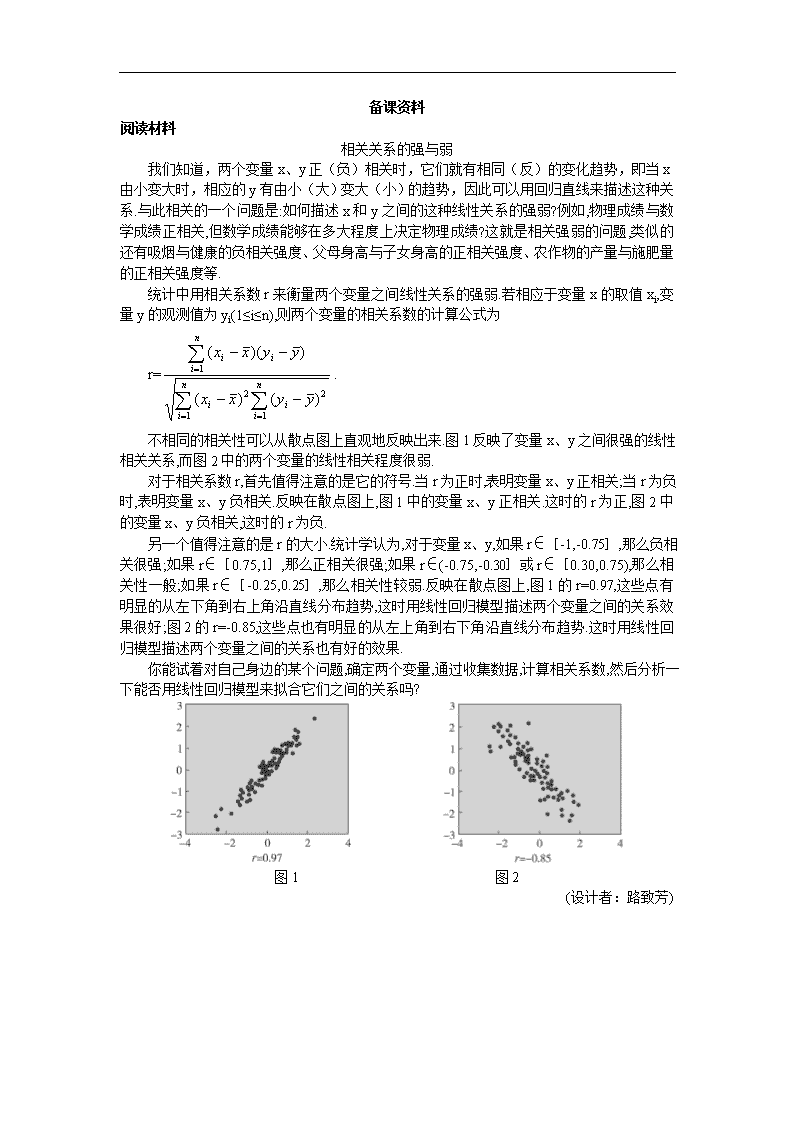
备课资料 阅读材料 相关关系的强与弱 我们知道,两个变量x、y正(负)相关时,它们就有相同(反)的变化趋势,即当x由小变大时,相应的y有由小(大)变大(小)的趋势,因此可以用回归直线来描述这种关系.与此相关的一个问题是:如何描述x和y之间的这种线性关系的强弱?例如,物理成绩与数学成绩正相关,但数学成绩能够在多大程度上决定物理成绩?这就是相关强弱的问题,类似的还有吸烟与健康的负相关强度、父母身高与子女身高的正相关强度、农作物的产量与施肥量的正相关强度等. 统计中用相关系数r来衡量两个变量之间线性关系的强弱.若相应于变量x的取值xi,变量y的观测值为yi(1≤i≤n),则两个变量的相关系数的计算公式为 r=. 不相同的相关性可以从散点图上直观地反映出来.图1反映了变量x、y之间很强的线性相关关系,而图2中的两个变量的线性相关程度很弱. 对于相关系数r,首先值得注意的是它的符号.当r为正时,表明变量x、y正相关;当r为负时,表明变量x、y负相关.反映在散点图上,图1中的变量x、y正相关.这时的r为正,图2中的变量x、y负相关,这时的r为负. 另一个值得注意的是r的大小.统计学认为,对于变量x、y,如果r∈[-1,-0.75],那么负相关很强;如果r∈[0.75,1],那么正相关很强;如果r∈(-0.75,-0.30]或r∈[0.30,0.75),那么相关性一般;如果r∈[-0.25,0.25],那么相关性较弱.反映在散点图上,图1的r=0.97,这些点有明显的从左下角到右上角沿直线分布趋势,这时用线性回归模型描述两个变量之间的关系效果很好;图2的r=-0.85,这些点也有明显的从左上角到右下角沿直线分布趋势.这时用线性回归模型描述两个变量之间的关系也有好的效果. 你能试着对自己身边的某个问题,确定两个变量,通过收集数据,计算相关系数,然后分析一下能否用线性回归模型来拟合它们之间的关系吗? 图1 图2 (设计者:路致芳)查看更多